☀️ 🌙

Метод рационализации

В данной статье мы рассмотрим основные ситуации, когда неравенство можно решать методом рационализации.

Метод рационализации — это метод, который позволяет (в определённых случаях) исходное неравенство заменить на равносильное ему рациональное неравенство (имеющее то же множество решений), которое решается методом интервалов.

Если у нас есть какое-то выражение \(f(x)\), которое совпадает по знаку с выражением \(g(x)\) (то есть они или оба положительны при одних и тех же значениях \(x\), или оба отрицательны при одних и тех же значениях \(x\), или она равны нулю при одних и тех же значениях \(x\)), то мы можем одно выражение заменить на другое.

Рассмотрим основные ситуации, когда можно использовать метод рационализации.

\(a^b-a^c\) совпадает по знаку с \(b-c\) при \(a>1\)

Функция \(y=a^x\) при \(a>1\) является монотонно возрастающей. Это означает, что:

если \(b>c\), то \(a^b>a^c\) (то есть из \(b-c>0\) следует \(a^b-a^c>0\))
если \(b<c\), то \(a^b<a^c\) (то есть из \(b-c<0\) следует \(a^b-a^c<0\))
если \(b=c\), то \(a^b=a^c\) (то есть из \(b-c=0\) следует \(a^b-a^c=0\))

То есть знаки выражений \(a^b-a^c\) и \(b-c\) совпадают.

Пример: \(4^x>2^{x^2} \Leftrightarrow \) \(2^{2x}>2^{x^2} \Leftrightarrow \) \(2x>x^2 \Leftrightarrow \) \(x\in(0;2)\)

Пример: \(\left(\dfrac{1}{2}\right)^{4 x^2-15 x+13}< 2^{3 x-4} \Leftrightarrow \) \(\left(2^{-1}\right)^{4x^2-15x+13}< 2^{3 x-4} \Leftrightarrow \) \(2^{-4x^2+15x-13}< 2^{3 x-4} \Leftrightarrow \) \(-4x^2+15x-13< 3x-4 \Leftrightarrow \) \(4x^2-12x+9>0 \Leftrightarrow \) \((2x-3)^2>0 \Leftrightarrow \) \(x\in\mathbb{R}/\{1,5\}\)

Для наглядности монотонности рассмотрим график функции \(y=2^x\). Все графики вида \(y=a^x\) при \(a>1\) имеют схожий вид. Как мы можем наблюдать, при увеличение значения \(x\) увеличивается и значение \(y\). Следовательно, это монотонно возрастающая функция. Тогда, если \(x_2>x_1\), то \(f(x_2)>f(x_1)\).

\(a^b-a^c\) совпадает по знаку с \(c-b\) при \(0<a<1\)

Функция \(y=a^x\) при \(0<a<1\) является монотонно убывающей. Это означает, что:

если \(c>b\), то \(a^b>a^c\) (то есть из \(c-b>0\) следует \(a^b-a^c>0\))
если \(c<b\), то \(a^b<a^c\) (то есть из \(c-b<0\) следует \(a^b-a^c<0\))
если \(b=c\), то \(a^b=a^c\) (то есть из \(b-c=0\) следует \(a^b-a^c=0\))

То есть знаки выражений \(a^b-a^c\) и \(c-b\) совпадают.

Пример: \(0,99^x>0,99^2\Leftrightarrow\) \(x<2\)

Пример: \(\left(\dfrac{1}{2}\right)^{4 x^2-15 x+13}<2^{3 x-4}\Leftrightarrow\) \(\left(\dfrac{1}{2}\right)^{4x^2-15x+13}<\left(2^{-1}\right)^{-(3x-4)}\Leftrightarrow\) \(\left(\dfrac{1}{2}\right)^{4x^2-15x+13}<\left(\dfrac{1}{2}\right)^{-3x+4}\Leftrightarrow\) \(4x^2-15x+13>-3x+4 \Leftrightarrow\) \(4x^2-12x+9>0\Leftrightarrow\) \((2x-3)^2>0\Leftrightarrow\) \(x\in\mathbb{R}/\{1,5\}\)

Для наглядности монотонности рассмотрим график функции \(y=\left(\dfrac{1}{2}\right)^x\). Все графики вида \(y=a^x\) при \(0<a<1\) имеют схожий вид. Как мы можем наблюдать, при увеличение значения \(x\) уменьшается значение \(y\). Следовательно, это монотонно убывающая функция. Тогда, если \(x_2>x_1\), то \(f(x_2)<f(x_1)\).

\(a^b-a^c\) совпадает по знаку с \((a-1)(b-c)\) при \(a>0\)

В общем случае оба предыдущих пункта сводятся к этому. Ведь если \(a>1\), то скобка \((a-1)>0\). Тогда, разделив \((a-1)(b-c)\) на неё, останется \(b-c\), как и в первой ситуации.

Если \(0<a<1\), то скобка \((a-1)<0\). Тогда, разделив \((a-1)(b-c)\) на \(|a-1|\), останется \(-(b-c)=c-b\), как и во второй ситуации.

Пример: \((x-1)^x>(x-1)^{x^2}\Leftrightarrow\) \(\left\{\begin{gathered}(x-1-1)(x-x^2)>0\hfill\\x-1>0\hfilll\end{gathered}\right.\Leftrightarrow\) \(x\in(1;2)\)

Следствие основного свойства.

\(a^x-1\) совпадает по знаку с \((a-1)x\) при \(a>0\)

Здесь необходимо представить единицу как \(a^0\). Тогда \(a^x-1=a^x-a^0\), что по методу рационализации заменяется на \((a-1)(x-0)=(a-1)x\).

\(\log_a b-\log_a c\) совпадает по знаку с \(b-c\) при \(a>1\), \(b,c>0\)

Функция \(y=\log_a x\) при \(a>1\) является монотонно возрастающей. Это означает, что:

если \(b>c\), то \(\log_a b>\log_a c\) (то есть из \(b-c>0\) следует \(\log_a b-\log_a c>0\))
если \(b<c\), то \(\log_a b<\log_a c\) (то есть из \(b-c<0\) следует \(\log_a b-\log_a c<0\))
если \(b=c\), то \(\log_a b=\log_a c\) (то есть из \(b-c=0\) следует \(\log_a b-\log_a c=0\))

То есть знаки выражений \(\log_a b-\log_a c\) и \(b-c\) совпадают.

Пример: \(\log _5(3 x-5)>\log _5(x+1)\Leftrightarrow\) \(\left\{\begin{gathered}3x-5>x+1\hfill\\3x-5>0\hfill\\x+1>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in(3;+\infty)\)

Пример: \(\log _3 {(8-6 x)} \leqslant \log _3 {2x} \Leftrightarrow\) \(\left\{\begin{gathered}8x-6\leqslant 2x\hfill\\8x-6>0\hfill\\2x>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in\left(\dfrac{3}{4};1\right]\)

Для наглядности монотонности рассмотрим график функции \(y=\log_2 x\). Все графики вида \(y=\log_a x\) при \(a>1\) имеют схожий вид. Как мы можем наблюдать, при увеличение значения \(x\) увеличивается и значение \(y\). Следовательно, это монотонно возрастающая функция. Тогда, если \(x_2>x_1\), то \(f(x_2)>f(x_1)\).

\(\log_a b-\log_a c\) совпадает по знаку с \(c-b\) при \(0<a<1\), \(b,c>0\)

Функция \(y=\log_a x\) при \(0<a<1\) является монотонно убывающей. Это означает, что:

если \(c>b\), то \(\log_a b>\log_a c\) (то есть из \(c-b>0\) следует \(\log_a b-\log_a c>0\))
если \(c<b\), то \(\log_a b<\log_a c\) (то есть из \(c-b<0\) следует \(\log_a b-\log_a c<0\))
если \(b=c\), то \(\log_a b=\log_a c\) (то есть из \(b-c=0\) следует \(\log_a b-\log_a c=0\))

То есть знаки выражений \(\log_a b-\log_a c\) и \(c-b\) совпадают.

Пример: \(\log _{0,2}(x-1) > \log _{0,2}(5-x) \Leftrightarrow\) \(\left\{\begin{gathered}x-1<5-x\hfill\\x-1>0\hfill\\5-x>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in(1;3)\)

Пример: \(\log _{\frac{1}{2}}(3 x-1)<\log _{\frac{1}{2}}(3-x) \Leftrightarrow\) \(\left\{\begin{gathered}3x-1>3-x\hfill\\3x-1>0\hfill\\3-x>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in(1;3)\)

Для наглядности монотонности рассмотрим график функции \(y=\log_{\frac{1}{2}} x\). Все графики вида \(y=\log_a x\) при \(0<a<1\) имеют схожий вид. Как мы можем наблюдать, при увеличение значения \(x\) уменьшается значение \(y\). Следовательно, это монотонно убывающая функция. Тогда, если \(x_2>x_1\), то \(f(x_2)<f(x_1)\).

\(\log_a b-\log_a c\) совпадает по знаку с \((a-1)(b-c)\) при \(a>0\), \(a\neq1\), \(b,c>0\)

Если \(0<a<1\), то скобка \((a-1)<0\). Тогда, разделив \((a-1)(b-c)\) на \(|a-1|\), останется \(-(b-c)=c-b\), как и во второй ситуации.

Пример: \(\log_x {(2-x)}>\log_x {(2x+1)}\Leftrightarrow\) \(\left\{\begin{gathered}(x-1)(2-x-(2x+1))>0\hfill\\x>0\hfill\\x\neq1\hfill\\2-x>0\hfill\\2x+1>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in\left(\dfrac{1}{3};1\right)\)

Следствие основного свойства.

\(\log_a b\) совпадает по знаку с \((a-1)(b-1)\) при \(a>0\), \(a\neq1\), \(b>0\)

Если у нас есть одиночный логарифм, то мы всегда можем вычесть из него ноль, а по определению логарифма \(0=\log_a 1\).

Поэтому \(\log_a b=\log_a b-\log_a 1\), что по методу рационализации заменяется на \((a-1)(b-1)\).

Пример: \(\log_{x+1} x<0 \Leftrightarrow\) \(\left\{\begin{gathered}(x+1-1)(x-1)<0\hfill\\x+1>0\hfill\\x+1\neq1\hfill\\x>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in(0;1)\)

Следствие основного свойства.

\(\log_a b-1\) совпадает по знаку с \((a-1)(b-a)\) при \(a>0\), \(a\neq1\), \(b>0\)

Здесь необходимо представить единицу как \(\log_a a\). Тогда \(\log_a b-1=\log_a b-\log_a a\), что по методу рационализации заменяется на \((a-1)(b-a)\).

Пример: \(\log_{x^2} {(x-1)}<1\Leftrightarrow\) \(\log_{x^2} {(x-1)}<\log_{x^2} {x^2}\Leftrightarrow\) \(\left\{\begin{gathered}(x^2-1)(x-1-x^2)<0\hfill\\x^2>0\hfill\\x^2\neq1\hfill\\x-1>0\hfill\end{gathered}\right.\Leftrightarrow\) \(x\in(1;+\infty)\)

Следствие основного свойства.

\(\log_a b-m\) совпадает по знаку с \((a-1)(b-a^m)\) при \(a>0\), \(a\neq1\), \(b>0\)

Здесь необходимо представить \(m\) как \(\log_a {a^m}\). Тогда \(\log_a b-m=\log_a b-\log_a {a^m}\), что по методу рационализации заменяется на \((a-1)(b-a^m)\).

Следствие основного свойства.

\(\log_a b+\log_a c\) совпадает по знаку с \((a-1)(bc-1)\) при \(a>0\), \(a\neq1\), \(b,c>0\)

Мы можем использовать метод рационализации только тогда, когда у нас разность логарифмов. Однако с суммой логарифмов можно провести некоторые операции и привести её к разности.

Для этого заменим знак плюс между ними на "минус на минус". То есть получим такое выражение: \(\log_a b - -\log_a c\). Далее один из минусов оставляем, а второй заносим в аргумент второго логарифма: \(\log_a b-\log_a {c^{-1}}=\log_a b-\log_a {\dfrac{1}{c}}\), что по методу рационализации заменяется на \((a-1)\left(b-\frac{1}{c}\right)=(a-1)\left(\dfrac{bc-1}{c}\right)\).

Ввиду того, что \(c>0\), знаменатель второй скобки никак не влияет на знак. Тогда исходная сумму логарифмов равносильна выражению \((a-1)(bc-1)\).

Можно рассуждать немного иначе, и сразу вынести минус из аргумента второго логарифма, то есть вместо \(\log_a c\) записать \(-\log_a {c^{-1}}=-\log_a \frac{1}{c}\). Тогда, подставляя это в исходную сумму, получим то же самое, что и в первом способе.

\(\sqrt{a}-\sqrt{b}\) совпадает по знаку с \(a-b\) при \(a,b \geqslant0\)

Для того, чтобы доказать данное утверждение, умножим исходное выражение \(\sqrt{a}-\sqrt{b}\) на выражение \(\sqrt{a}+\sqrt{b}\), которое всегда положительно.

В результате получим \((\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})=\) \(\left(\sqrt{a}\right)^2-\left(\sqrt{b}\right)^2=\) \(a-b\)

Знак выражения никак не поменялся, ведь мы умножали на выражение, которое всегда больше нуля (в случае, если \(\sqrt{a}+\sqrt{b}=0\), то тогда \(a=b=0\)).

Иначе говоря: разность корней заменяем на разность подкоренных выражений на ОДЗ.

Следствия основного свойства.

\(\sqrt{a}-b\) совпадает по знаку с \(a-b^2\) при \(a,b \geqslant0\)

Рассуждая аналогично: \((\sqrt{a}-b)(\sqrt{a}+b)=\) \(\left(\sqrt{a}\right)^2-b^2=\) \(a-b^2\)

\(a-\sqrt{b}\) совпадает по знаку с \(a^2-b\) при \(a,b \geqslant0\)

Рассуждая аналогично: \((a-\sqrt{b})(a+\sqrt{b})=\) \(a^2-\left(\sqrt{b}\right)^2=\) \(a^2-b\)

\(|a|-|b|\) совпадает по знаку с \((a-b)(a+b)\)

Для того, чтобы доказать данное утверждение, умножим исходное выражение \(|a|-|b|\) на выражение \(|a|+|b|\), которое всегда положительно.

В результате получим \((|a|-|b|)(|a|+|b|)=\) \(|a|^2-|b|^2=\) \(a^2-b^2=\) \((a-b)(a+b)\).

Знак выражения никак не поменялся, ведь мы умножали на выражение, которое всегда больше нуля (в случае, если \(|a|+|b|=0\), то тогда \(a=b=0\)).

Иначе говоря: разность модулей заменяем на разность квадратов.

Здесь следует помнить, что \(x^2\) и \(|x|^2\) - это одно и то же. Ведь первое выражение всегда неотрицательно, и значит, если мы поставим ещё и модуль, то ничего не поменяется. В обратную сторону работает точно так же.

Следствие основного свойства.

И, если заранее известно, что \(m\geqslant0\), то \(m\) можно заменить на \(|m|\). Поэтому имеют место быть следующие следствия.

\(|a|-b\) совпадает по знаку с \((a-b)(a+b)\) при \(b\geqslant0\)

Так как \(b\geqslant0\), то \(b=|b|\). Тогда \(|a|-b=|a|-|b|\), что совпадает по знаку с \((a-b)(a+b)\).

\(a-|b|\) совпадает по знаку с \((a-b)(a+b)\) при \(a\geqslant0\)

Так как \(a\geqslant0\), то \(a=|a|\). Тогда \(a-|b|=|a|-|b|\), что совпадает по знаку с \((a-b)(a+b)\).

Метод рационализации можно использовать только если выражение сравнивается с нулём, а также выражение состоит из произведения или частного скобок (или отдельных множителей). То есть условия такие же, как и для использования метода интервалов.

Если есть неравенство \(\dfrac{5^x-5^2}{\log_2{2x}-\log_2({x^2})}\geqslant1\), то нельзя преобразовать числитель и знаменатель в равносильные им выражения по методу рационализации, ведь общее выражение сравнивается с единицей, а не с нулём. Так что здесь нельзя использовать рационализацию.

Если есть неравенство \(\dfrac{\log_2 x-2}{3^x-9}+\log_3 x\leqslant0\), то нельзя преобразовать числитель, знаменатель и отдельно стоящий логарифм в равносильные им выражения по методу рационализации, ведь исходное выражение состоит из суммы дроби и логарифма, а нам нужно, чтобы было произведение или частное скобок, а не сумма.

Нельзя ей пользоваться и в примере \(\dfrac{\log_2{(2x+3)}-\log_2{x}}{x+1}+\dfrac{3^x-3}{x+5}>0\), ведь у нас записана сумма дробей.

Рационализацию можно использовать только тогда, когда слева единственная дробь, в которой всё разбито на множители, или просто произведение множителей, а справа стоит ноль.

Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/

Разберём примеры, которые легко решаются через метод рационализации.

Пример 1. \(\dfrac{3^{x}-3^{2}}{x-1}>0\)

Так как справа стоит ноль, а \(y=3^t\) - возрастающая функция, то \(3^x-3^2\) будет иметь такой же знак по отношению к нулю, как и разность степеней, то есть \(x-2\). Поэтому, по методу рационализации неравенство принимает вид:

\(\dfrac{x-2}{x-1}>0\)

Так что исходное и получившееся неравенства имеют одинаковые решения, так как мы просто сделали равносильный переход.

Ответ: \(x \in (-\infty;\ 1)\cup(2;\ +\infty)\)

Пример 2. \(\dfrac{\log _2(x+2)-\log _2 2 x}{x} \geqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
x+2>0\hfill\\
2x>0\ \hfill
\end{gathered}
\right. \hspace{2mm} \Leftrightarrow \hspace{2mm}
\left\{
\begin{gathered}
x>-2\hfill\\
x>0\ \hfill
\end{gathered}
\right.\hspace{2mm} \Leftrightarrow \hspace{2mm}
x>0\)

Так как \(y=\log _2 t\) - возрастающая функция, то разность логарифмов в сравнение с нулём имеет тот же знак, что и разность их аргументов.

Поэтому преобразуем неравенство:

\(\dfrac{x+2-2 x}{x} \geqslant 0\)

\(\dfrac{-x+2}{x} \geqslant 0\)

\(-\dfrac{x-2}{x}\geqslant0\)

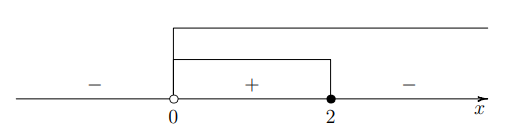
Ответ: \(x \in (0;\ 2]\)

Пример 3. \(\dfrac{\sqrt{4 x^2+2}-\sqrt{x+5}}{3^x-3^5} \geqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
4x^2+2>0\hfill\\
x+5>0 \hfill
\end{gathered}
\right. \)

\(y=\sqrt{t}\) - возрастающая функция, \(y=3^x\) - тоже возрастающая функция. Поэтому в сравнение с нулём неравенство равносильно следующему:

\(\dfrac{(4 x^2+2)-(x+5)}{x-5} \geqslant 0\)

Решаем неравенство методом интервалов, и, учитывая ограничения, получаем ответ.

Ответ: \(x \in \left[-\dfrac{3}{4};\ 1\right]\cup(5;\ +\infty)\)

Пример 4. \(\dfrac{\log _2 x}{x+1}>0\)

Ограничения: \(x>0\)

Чтобы преобразовать числитель, вычтем из него ноль, помня, что \(0=\log_2 1\)

\(\dfrac{\log _2 x-0}{x+1}>0\)

\(\dfrac{\log _2 x-\log _2{1}}{x+1}>0\)

\(\dfrac{x-1}{x+1}>0\)

Ответ: \(x \in (1;\ +\infty)\)

Пример 5. \((x^2+3 x-4) \cdot \log _3 x \leqslant 0\)

Ограничение: \(x>0\)

Как и в предыдущем примере, если есть отдельно стоящий логарифм и нам нужно определить его знак, то из него надо вычесть ноль.

\((x+4)(x-1)\left(\log _3 x-\log _3 1\right) \leqslant 0\)

\(y=\log _3 t\) - возрастающая функция.

\((x+4)(x-1)(x-1) \leqslant 0\)

Ответ: \(x\in\{1\}\)

Если основание логарифма неизвестно, то лучше всего перейти к новому основанию по формуле \(\log _b a=\dfrac{\log _c a}{\log _c b}\) (основание может быть любым, следует смотреть по примеру, к какому основанию удобнее перейти).

То есть в неравенстве \(\log _x(3+x)>\log _x 2 x\) нельзя отбросить логарифмы и сказать, что \(3+x>2x\). Ведь если основание \(x>1\), то знак неравенства сохранится, а если основание \(0<x<1\), то знак нужно будет поменять.

Поэтому всегда, когда основание логарифма неизвестно, переходим к новому основанию: \(\dfrac{\log _2(3+x)}{\log _2 x}>\dfrac{\log _2(2 x)}{\log _2 x} \Leftrightarrow\) \(\dfrac{\log _2(3+x)-\log _2(2 x)}{\log _2 x}>0 \Leftrightarrow\) \(\dfrac{(3+x)-2 x}{x-1}>0\)

Конечно, можно рассмотреть 2 случая для основания:

\(\left[
\begin{gathered}
\left\{
\begin{gathered}
x>1\hfill\\
3+x>2x\hfill
\end{gathered}
\right. \hfill\\
\left\{
\begin{gathered}
0<x<1\hfill\\
3+x<2x\hfill
\end{gathered}
\right.
\end{gathered}
\right.\)

В первом случае знак неравенства сохраняется, а во втором меняется на противоположенный. Однако этот способ достаточно долгий.

И также можно пользоваться общим случаем рационализации: \(\log_x{a}-\log_x{b} \ \text{V}\ 0 \Leftrightarrow (x-1)(a-b) \ \text{V}\ 0\) (где \(V\) - любой знак сравнения).

То есть \(\log _x(3+x)>\log _x 2 x \Leftrightarrow\) \(\log _x(3+x)-\log _x 2 x>0 \Leftrightarrow\) \((x-1)(3+x-2x)>0 \Leftrightarrow\) \((x-1)(x-3)<0\)

Однако бывают случаи, когда основание неизвестно, но мы можем сразу отбросить логарифмы.

Например: \(\log _{x^2+1}(x-5)>\log _{x^2+1}(2 x)\).

Здесь в основание есть \(x\), но мы знаем, что \(x^2\geqslant0\) для любого \(x\). То есть \(x^2=0\) - это минимум, который может быть. Тогда \(x^2+1\) минимум может равняться 1. Но, так как \(x\) находится в аргументе, то он не может равняться нулю, соответственно \(x^2+1>1\).

Мы выяснили, что для любого \(x\) из области определения основание логарифмов строго больше 1. Значит, это возрастающие функции, и исходное неравенство равносильно следующему: \(x-5>2x\).

Рассмотрим ещё один пример: \(\log _{1-\frac{1}{x^2}}(x-5)>\log _{1-\frac{1}{x^2}}(2 x)\).

Также посмотрим на основания логарифмов: \(\dfrac{1}{x^2}>0\) всегда. Тогда \(-\dfrac{1}{x^2}<0\). Следовательно, основание \(1-\dfrac{1}{x^2}<1\), так как мы к единице прибавляем всегда отрицательное выражение. Тогда можем сразу записать, что \(x-5<2x\). И не забываем про ограничения.

Пример 6. \(\dfrac{(x-1) \log _{x}(3+x)}{5^x-4} \geqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
3+x>0\hfill\\
x>0 \hfill\\
x\neq 1\hfill
\end{gathered}
\right. \)

Перейдём к новому основанию.

\(\dfrac{(x-1)\log_2(3+x)}{(5^x-4)\log_2 x} \geqslant 0\)

\(\dfrac{(x-1)(\log_2(3+x)-0)}{(5^x-4)(\log_2 x -0)} \geqslant 0\)

\(\dfrac{(x-1)(\log_2(3+x)-\log_2{1})}{(5^x-5^{\log_5{4}})(\log_2 x -\log_2{1})} \geqslant 0\)

\(y=\log _2 t\) - возрастающая функция.

\(y=5^t\) - возрастающая функция.

\(\dfrac{(x-1)(3+x-1)}{\left(x-\log _5 4\right)(x-1)} \geqslant 0\)

Ответ: \(x\in(\log_5{4};\ 1)\cup(1;\ +\infty)\)

Пример 7. \(\dfrac{\log _2(8 x) \cdot \log _3(27 x)}{x^2-|x|} \leqslant 0\)

Так как из-за логарифмов ограничение состоит из \(x>0\), то в знаменателе модуль сразу раскроется без изменения знака.

\(\dfrac{\left.\log _2(8 x) \cdot \log _3(27 x\right)}{x(x-1)} \leqslant 0\)

Далее действуем по знакомой схеме: вычитаем из каждого логарифма нули и применяем рационализацию.

Ответ: \(x\in \left(0;\ \dfrac{1}{27}\right]\cup\left[\dfrac{1}{8};\ 1\right)\)

Пример 8. \(\left|x^2-1\right|-|2 x-2|<0\)

По методу рационализации заменим разность модулей на разность квадратов.

\(\left(x^2-1\right)^2-\left(2x-2\right)^2<0\)

\(\left((x^2-1)-(2x-2)\right)\left((x^2-1)+(2x-2)\right)<0\)

\((x^2-1-2x+2)(x^2-1+2x-2)<0\)

\((x^2-2x+1)(x^2+2x-3)<0\)

\((x-1)^2(x-1)(x+3)<0\)

\((x-1)^3(x+3)<0\)

Ответ: \(x \in(-3 ; 1)\)

Пример 9. \(\dfrac{\log _2\left(2 x^2-17 x+35\right)-1}{\log _7(x+6)} \leqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
2x^2-17 x+35>0\hfill\\
x+6>0 \hfill
\end{gathered}
\right.
\Leftrightarrow\) \(\left\{
\begin{gathered}
2(x-5)\left(x-\dfrac{7}{2}\right)>0\hfill\\
x>-6 \hfill
\end{gathered}
\right.\)

\(\dfrac{\log _2(2 x^2-17 x+35)-\log _2 2}{\log _7(x+6)-\log _7 1} \leqslant 0\)

\(y=\log_2{t}\) - возрастающая функция

\(y=\log_7{t}\) - возрастающая функция

\(\dfrac{2 x^2-17 x+35-2}{x+6-1} \leqslant 0\)

\(\dfrac{2 x^2-7 x+33}{x+5} \leqslant 0\)

\(2x^2-17x+33=0 \Rightarrow\) \(m^2-17 m+66=0 \hspace{2mm}\Rightarrow\)

\(\left[
\begin{gathered}
m=11\hfill\\
m=6 \hfill
\end{gathered}
\right.
\Rightarrow\) \(\left[
\begin{gathered}
x=\dfrac{11}{2}\hfill\\
x=3 \hfill
\end{gathered}
\right. \)

\(\dfrac{2\left(x-\dfrac{11}{2}\right)(x-3)}{x+5} \leqslant 0\)

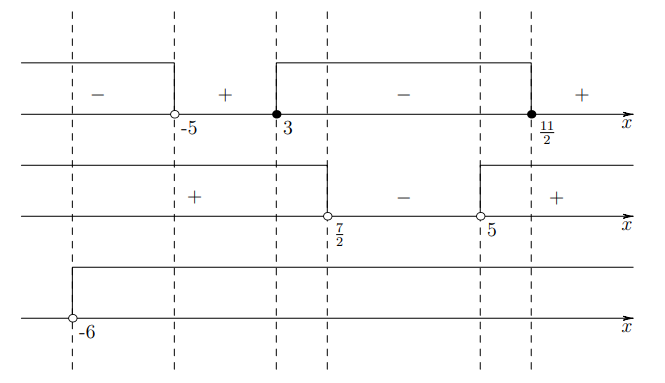
Ответ: \(x\in(-6;\ -5)\cup\left[3;\ \dfrac{7}{2}\right)\cup\left(5;\dfrac{11}{2}\right]\)

В этом примере при решение квадратного уравнения мы воспользовались методом "переброски", подробнее про который вы можете почитать здесь.

Пример 10. \(\log _{x+1}(x-1) \cdot \log _{x+1}(x+2) \leqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
x+1>0\hfill\\
x+1 \neq 1 \hfill\\
x-1>0 \hfill\\
x+2>0 \hfill
\end{gathered}
\right.\Leftrightarrow
x>1\)

\(\dfrac{\log _2(x-1)}{\log _2(x+1)} \cdot \dfrac{\log _2(x+2)}{\log _2(x+1)} \leqslant 0\)

Так как здесь присутствуют одни множители, то можем сразу использовать метод рационализации

\(\dfrac{(\log _2(x-1)-\log _2 1)(\log _2(x+2)-\log _2 1)}{(\log _2(x+1)-\log_2{1})^2} \leqslant 0\)

\(\dfrac{((x-1)-1)((x+2)-1)}{((x+1)-1)^2} \leqslant 0\)

\(\dfrac{(x-2)(x+1)}{x^2} \leqslant 0\)

Также здесь можно было перейти к равносильной системе. Так как в знаменателе выражение в квадрате, то оно не влияет на знак, поэтому можем на него домножить. Главное, чтобы знаменатель не был равен нулю.

\(\dfrac{(\log _2(x-1)-\log _2 1)(\log _2(x+2)-\log _2 1)}{(\log _2(x+1)-\log_2{1})^2} \leqslant 0 \Leftrightarrow\) \(\left\{
\begin{gathered}
((x-1)-1)((x+2)-1)) \leqslant 0\hfill\\
\log _2(x+1) \neq 0 \hfill
\end{gathered}
\right. \Leftrightarrow\) \(\left\{
\begin{gathered}
(x-2)(x+1) \leqslant 0\hfill\\
x+1 \neq 1 \hfill
\end{gathered}
\right.\)

Ответ: \(x\in(1;\ 2]\)

Вот так это работает на более простом примере: \(\dfrac{x-3}{x^2} \geqslant 0\).

А через равносильную систему получаем:

\(\left\{
\begin{gathered}
x-3 \geqslant 0\hfill\\
x^2 \neq 0 \hfill
\end{gathered}
\right. \Leftrightarrow
\left\{
\begin{gathered}
x \geqslant 3\hfill\\
x \neq 0 \hfill
\end{gathered}
\right.\)

Пример 11. \(\dfrac{\log _x(x-3)}{\log _{x^2}(5-x)-1} \geqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
x>0\hfill\\
x\neq 1 \hfill\\
x^2>0\hfill\\
x^2\neq 1 \hfill\\
x-3>0 \hfill\\
5-x>0 \hfill
\end{gathered}
\right. \)

Переходим к новому основанию, упрощаем выражение и используем рационализацию.

\(\dfrac{\dfrac{\log _2(x-3)}{\log _2 x}}{\dfrac{\log _2(5-x)}{\log _2 x^2}-1} \geqslant 0\)

\(\dfrac{\dfrac{\log _2(x-3)}{\log _2 x}}{\dfrac{\log _2(5-x)-\log _2 x^2}{\log _2 x^2}} \geqslant 0\)

\(\dfrac{\log _2(x-3)}{\log _2 x} \cdot \dfrac{\log _2 x^2}{\log _2(5-x)-\log _2 x^2} \geqslant 0\)

\(\dfrac{(x-3-1)\left(x^2-1\right)}{(x-1)\left(5-x-x^2\right)} \geqslant 0\)

Ответ: \(x \in(3;\ 4]\)

Пример 12. (ЕГЭ 2023). \(\log _3^2(x-4)-\log _3^2(x-6) \leqslant 0\)

Ограничения:

\(\left\{
\begin{gathered}
x-6>0\hfill\\
x-4>0 \hfill
\end{gathered}
\right. \hspace{2mm}\Leftrightarrow\hspace{2mm}
x>6\)

По формуле для разности квадратов \(A^2-B^2=(A-B)(A+B)\) раскладываем неравенство:

\((\log _3(x-4)-\log _3(x-6))(\log _3(x-4)+\log _3{(x-6}) )\leqslant 0\)

Чтобы использовать метод рационализации, нужно во второй скобке получить знак минус. Для этого плюс представим как "минус на минус". Один из минусов оставим, а второй занесём в степень аргумента логарифма. Тогда аргумент из \((x-6)\) превратится в \((x-6)^{-1}=\dfrac{1}{x-6}\).

\((\log _3(x-4)-\log _3(x-6))\left(\log _3(x-4)-\log _3\left(\dfrac{1}{x-6}\right)\right) \leqslant 0\)

\(y=\log _3 t\) - возрастающая функция.

\(((x-4)-(x-6))\left(x-4-\dfrac{1}{x-6}\right) \leqslant 0\)

\(2\left(\dfrac{x^2-6 x-4 x+24-1}{x-6}\right) \leqslant 0\)

\(\dfrac{x^2-10 x+23}{x-6} \leqslant 0\)

\(x^2-10 x+23=0\)

\(\dfrac{D}{4}=25-23=2\)

\(x=5 \pm \sqrt{2}\)

\(\dfrac{(x-(5+\sqrt{2}))(x-(5-\sqrt{2})}{x-6} \leqslant 0\)

Ответ: \(x \in (6;\ 5+\sqrt{2}]\)

В этом примере при решение квадратного уравнения мы воспользовались формулой \(\dfrac{D}{4}\), подробнее про которую вы можете почитать здесь.

Пример 13. \(\dfrac{\log _2 x-\log _3 x}{x-5}>0\)

Вначале, так как основания логарифмов разные, переходим к новому основанию.

\(\dfrac{\log _2 x-\dfrac{\log _2 x}{\log _2 3}}{x-5}>0\)

\(\dfrac{\log _2 x\left(1-\dfrac{1}{\log _2 3}\right)}{x-5}>0\)

\(\dfrac{\log _2 x(\log_2 3-1)}{(x-5)\log _2 3}>0\)

Так как \(\log_2 3>1\), то \((\log_2 3-1)>0\). Тогда обе части неравенства разделим на \(\dfrac{\log_2 3-1}{\log_2 3}>0\).

\(\dfrac{\log_2 x}{x-5}>0\)

\(\dfrac{x-1}{x-5}>0\)

C учётом ОДЗ получаем ответ: \(x \in (0;\ 1) \cup (5;\ +\infty)\)

Дополнительные примеры для тренировки

Пример 1. \(\dfrac{\log_x{(x-2)}}{x+2}>0\)

Пример 2. \(\dfrac{\log_2{x}\cdot\log_7{(x+3)}}{(3^x-5)\cdot5^x\geqslant0}\)

Пример 3. \(\dfrac{\left(3^x-9\right)\left(\log _5(6-x)-1\right)}{|x|-4}<0\)

Подсказка: чтобы упростить знаменатель, воспользуйтесь тем, что \(4=|4|\)

Пример 4. \(x^{x^2+3 x-4}<x^{5-x}\)

Подсказка: не забудьте, что у показательной функции основание всегда строго больше нуля

Пример 5. \(\left|x^2-13 x+35\right|>\left|35-x^2\right|\)

Пример 6. \(\sqrt{x^2+5 x}<\sqrt{1-x^2+4 x}\)

Пример 7. \(\sqrt{25-x^2}\cdot\log_{x+5}{2}\leqslant0\)

Пример 8. \(\log_5{((3-x)(x^2+2))}\geqslant\log_5{(x^2-7x+12)}+\log_5{(5-x)}\)

Пример 9. \(\dfrac{25^{x^2+x-10}-(0,2)^{x^2-2x-7}}{0,5\cdot4^{x-1}-1}\leqslant0\)

Пример 10. \(2\log_2({x\sqrt{5}})-\log_2{\left(\dfrac{x}{1-x}\right)}\leqslant\log_2{\left(5x^2+\dfrac{1}{x}-2\right)}\)

Пример 11. \(\dfrac{\log_2{x^2}-\log_3{x^2}}{\log^2_6{(2x^2-10x+12,5)}+1}\geqslant0\).

Ответы к примерам для тренировки

Пример 1. \(x \in (3;\ +\infty)\)

Пример 2. \(x \in (0;\ 1]\cup(\log_3{5};\ +\infty)\)

Пример 3. \(x\in(-\infty;-4)\cup(1;2)\cup(4;6)\)

Пример 4. \(x \in(1 ;-2+\sqrt{13})\)

Пример 5. \(x \in(-\infty ; 0) \cup\left(5 \frac{5}{13} ; 6,5\right)\)

Пример 6. \(x \in[0 ; 0,5)\)

Пример 7. \(x \in (-5;\ -4)\cup\{5\}\)

Пример 8. \(x \in [2;\ 3)\)

Пример 9. \(x \in (-\infty;\ -3]\cup\left(\dfrac{3}{2};\ 3\right]\)

Пример 10. \(x \in \left(0;\ \dfrac{\sqrt{5}}{5}\right]\cup\left[\dfrac{1}{2};\ 1\right)\)

Пример 11. \(x \in (-\infty;\ -1]\cup\left[1;\ \dfrac{5}{2}\right)\cup\left(\dfrac{5}{2};\ +\infty\right)\)

Теория к первой части ЕГЭ

Банк задач по первой части ЕГЭ

Другие статьи по важным темам

План подготовки к ЕГЭ