Метод интервалов
Метод интервалов
Чтобы решить неравенство методом интервалов, нужно равносильными преобразованиями привести неравенство или к виду \(\dfrac{(x-x_1)^m(x-x_2)^n\cdots}{(x-x_3)^k(x-x_4)^l\cdots}\) V 0, или к виду \((x-x_1)^m(x-x_2)^n\cdots\) V 0, где \(m,n,k,l\) - любые натуральные числа, V - любой знак сравнения. Иначе говоря, нам нужно получить произведение или частное скобок (множителей) слева, а справа получить ноль
Далее находим, когда каждая из скобок равна нулю, и отмечаем эти точки на координатной прямой. Чтобы определить знак на промежутке, надо любую точку из него подставить в исходное неравенство.
Пример 1. \((x-2)(x-3)<0\)
Скобка \(x-2\) равна нулю при \(x=2\), а скобка \(x-3\) равна нулю при \(x=3\). Наносим эти точки на координатную прямую. Так как неравенство строгое, то точки выколоты.
Для проверки знака можно из самого правого промежутка взять точку \(x=5\). Тогда при подстановке в исходное неравенство получаем \((5-2)(5-3)\), что будет больше нуля. Поэтому на промежутке \((3; +\infty)\) ставится знак плюс. Далее, так как ни одна из скобок не возводится в чётную степень, знаки чередуются справа налево.

Так как в исходном неравенстве просили найти промежутки, где будет стоять минус, что в ответ идёт \(x \in(2 ;\ 3)\)
Пример 2. \((x-5)(x-3)>0\)
Для того, чтобы каждый раз не подставлять точку и не проверять знак на промежутке, удобнее всего делать так. Если в исходном неравенстве перед всеми \(x\) стоит знак плюс (если нет знака, значит стоит плюс), то самый правый промежуток всегда будет положительным. Далее, при переходе через корень, знаки чередуются.

Ответ: \(x \in (-\infty;\ 3) \cup (5;\ +\infty)\)
Пример 3. \((3-x)(x+5)>0\)
В данном случае в первой скобке перед \(x\) стоит минус. Поэтому при подстановке больших чисел в эту скобку, она будет отрицательной, а вторая положительной. Поэтому если перед \(x\) в одной скобке (или в нечётном количестве скобок) есть минус, то правый промежуток будет отрицательным. Далее справа налево знаки чередуются.

Это неравенство также можно решить, если умножить обе части неравенства на \(-1\) и занести \(-1\) в первую скобку. Тогда слева получится произведение \((x-3)(x+5)\), и, так как мы умножили на отрицательное число, то знак поменяется на противоположенный. То есть получится неравенство \((x-3)(x+5)<0\). Сделали это для того, чтобы перед всеми \(x\) стояли плюсы и правый промежуток был положительным.

В любом случае получаем ответ: \(x \in (-5;\ 3)\)
Пример 4. \((2x+5)(x-2)>5\)
Здесь нельзя сразу использовать метод интервалов, так как неравенство ещё не приведено для него, ведь справа не ноль. Поэтому вначале раскроем скобки и приведём неравенство к стандартному виду.
\(2x^2-4x+5x-10-5>0\)
\(2x^2+x-15>0\)
\(2x^2+x-15=0\)
\(\left[
\begin{gathered}
x=-3\hfill\\
x=2,5\hfill
\end{gathered}
\right.\)
\(2(x+3)(x-2,5)>0\)
\((x+3)(x-2,5)>0\)
Теперь неравенство готово, и мы можем чертить координатную прямую с точками -3 и 2,5.

Ответ: \(x\in(-\infty ;-3) \cup\left(\dfrac{5}{2} ; \infty\right)\)
Пример 5. \(\dfrac{x-2}{x-3} \leqslant 0\)
Если мы решаем неравенство методом интервалов, то ОДЗ писать не нужно. Действуя по алгоритму, определяем, что скобки равны нулю при \(x=2\) и \(x=3\). Неравенство нестрогое, поэтому точка \(x=2\) будет нам подходить, ведь при подстановке получаем \(0\leqslant0\), что верно. Поэтому точку \(x=2\) закрашиваем на оси. А вот точка \(x=3\) будет выколота, несмотря на знак неравенства, так как эта скобка находится в знаменателе. В этом и есть ОДЗ: \(x\neq3\). Поэтому, если решать неравенство методом интервалов, то отдельно ОДЗ прописывать не нужно.

Дальше решаем, как и предыдущие неравенства: везде перед \(x\) стоит плюс - правый промежуток положительный - знаки чередуются - берём промежуток со знаком минус, а также точку \(x=2\). Поэтому ответ будет \(x \in [2;\ 3)\)
Пример 6. \((x-2)^2(x-3) \geqslant 0\)
Рассмотрим пример, где скобка возводится в квадрат. В самом начале наносим на прямую точки, причём обе будут закрашены, ведь неравенство нестрогое, а знаменателя нет. Так как скобка \(x-2\) находится в квадрате, то она никак не будет влиять на знак (так будет со всеми чётными степенями (ноль - чётное число)), потому что скобка в любой чётной степени всегда неотрицательна. Поэтому над данной скобочкой ставим опознавательный знак: петелька, флажочек, восклицательный знак. Это обозначает, что, переходя через это число, знак неравенства меняться не будет.

Не забываем, что в ответ нужно включить не только правый промежуток, но и точку \(x=2\), ведь неравенство нестрого, и, подставив эту точку, получим верное неравенство. Все закрашенные точки обязательно включаем в ответ, даже если они не входят в промежуток! Это очень распространённая ошибка - не забывайте проверять те точки, над которыми стоит петелька!
Ответ: \(x \in\{2\} \cup[3 ;\ +\infty)\)
Пример 7. Если в конце получится такая координатная прямая, то все выделенные промежутки и все закрашенные точки пойдут в ответ.

Поэтому ответ: \(x \in [0 ;\ 5] \cup\{6\} \cup(7;\ 8)\)
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Пример 8. \((x-2)^4(x-3)^5 \leqslant 0\)
Здесь следует помнить, что если скобка в чётной степени, то, переходя через неё, знак не поменяется, и над ней надо поставить петельку. Если скобка находится в нечётной степени, то это аналогично первой степени, поэтому с этой скобкой ничего не делаем. Решение неравенства \((x-2)^{20}(x-3)^{553} \leqslant 0\) и исходного аналогичны.

Ответ: \(x \in (-\infty;\ 3]\). Записывать два промежутка и отдельно точку \(x=2\) не имеет смысла, так как она и так входит в получившийся промежуток.
Пример 9. \(\dfrac{(2 x-4)^5(x-3)^2}{(1-x)} \geqslant 0\)
Алгоритм решения такой. Сначала находим, что скобки равны нулю, при \(2x-4=0 \Leftrightarrow x=2\); \(x=3\) и \(x=1\). Точки \(x=2\) и \(x=3\) закрашиваем, точку \(x=1\) выкалываем. Над \(x=3\) ставим петельку. Всего в скобках присутствует один минус, поэтому правый промежуток отрицательный, далее чередуем, не забывая про петельку.

Ответ: \(x \in(1 ;\ 2] \cup\{3\}\)
Пример 10. \(\dfrac{x^2+3x-4}{(x-1)(x-2)} \geqslant 0\)
Если при решение неравенства мы сталкиваемся с квадратным трёхчленом вида \(ax^2+bx+c\), то нужно отдельно приравнять его к нулю (\(ax^2+bx+c=0)\), найти его корни \(x_1\) и \(x_2\), и записать его в виде \(a(x-x_1)(x-x_2)\). Тогда в исходном неравенстве вместо него мы получим произведение скобок.
В числителе квадратный трёхчлен \(x^2+3x-4\). По теореме Виета находим его корни \(x_1=1\) и \(x_2=-4\). Тогда его можно записывать в виде \((x-1)(x+4)\). И исходное неравенство принимает вид \(\dfrac{(x-1)(x+4)}{(x-1)(x-2)} \geqslant 0\)
Получилось, что скобка \(x-1\) есть как в числителе, так и в знаменателе. Закрашивать её нельзя, ведь она находится в знаменателе. И там, и там она находится в первой степени. Поэтому, по свойству степеней итоговая степень данной скобки будет равна нулю. А так как ноль - чётное число, то над корнем \(x=1\) на прямой нужно будет поставить петельку. Например, если в неравенстве будет частное \(\dfrac{(x-5)^6}{(x-5)^3}\), то итоговая степень этой скобки равна трём, значит, петельку ставить не нужно, но точку не забываем выколоть.
Можно действовать иначе: сократить эту скобку в числителе и знаменателе, но при этом нужно записать, что она не равна нулю, то есть \(x\neq1\) (так как на ноль делить и сокращаться нельзя). Однако тогда нужно не забыть в конце вернуться и выколоть эту точку!

Ответ: \(x \in (-\infty;\ -4] \cup (2;\ +\infty)\)
Пример 11. \(\dfrac{(x-2)^2(x-3)^6}{(-x^2+6x+7)^4} \geqslant 0\)
Для упрощения следующего неравенства нужно понимать, что \((-x)^2=x^2\).
И поэтому выражение \((-a-b)^2\) можно преобразовать так: \((-a-b)^2=(-(a+b))^2=(a+b)^2\).
И также: \((3-x)^2=(x-3)^2\)
\((a-b)^2=(b-a)^2\)
\((-x^2+5 x-7)^2=(x^2-5 x+7)^2\)
Поэтому исходное неравенство преобразуем так: \(\dfrac{(x-2)^2(x-3)^6}{(x^2-6x-7)^4} \geqslant 0 \Leftrightarrow\) \(\dfrac{(x-2)^2(x-3)^6}{((x-7)(x+1))^4}\geqslant 0 \Leftrightarrow\) \(\dfrac{(x-2)^2(x-3)^6}{(x-7)^4(x+1)^4}\geqslant 0\)

Ответ: \(x \in (-\infty;\ -1) \cup(-1 ;\ 7) \cup(7;\ +\infty)\)
Пример 12. \((x^2-9)(x+1)\geqslant0\)
Данное неравенство, как и все предыдущие, будет решать методом интервалов, поэтому нам нужно получить произведение скобок, в каждой из которых линейная функция. Поэтому, пользуясь формулой разности квадратов \(a^2-b^2=(a-b)(a+b)\) получим такое неравенство: \((x-3)(x+3)(x+1)\geqslant0\). Далее решаем обычным методом интервалов.

Ответ: \(x \in [-3;\ -1] \cup [3;\ +\infty)\)
Пример 13. \(\dfrac{\left(9-2 x^2\right) x}{(x-5)^4} \leqslant 0\)
Первым делом, чтобы избавить от минуса перед \(x^2\), умножим обе части неравенства на \(-1\), тогда получим следующее:
\(\dfrac{(2x^2-9)x}{(x-5)^4}\geqslant0 \Leftrightarrow\) \(\dfrac{2\left(x^2-\dfrac{9}{2}\right)x}{(x-5)^4}\geqslant0 \Leftrightarrow\) \(\dfrac{2\left(x^2-\left(\sqrt{\dfrac{9}{2}}\right)^2\right)x}{(x-5)^4}\Leftrightarrow\) \(\dfrac{2\left(x-\sqrt{\dfrac{9}{2}}\right)\left(x+\sqrt{\dfrac{9}{2}}\right)x}{(x-5)^4}\geqslant0 \Leftrightarrow\) \(\dfrac{2\left(x-\dfrac{3}{\sqrt{2}}\right)\left(x+\dfrac{3}{\sqrt{2}}\right)x}{(x-5)^4}\geqslant0\)
При решение неравенств лучше использовать именно метод интервалов, а не обобщённый метод интервалов. То есть нельзя сразу приравнять все скобки к нулю. Да, мы получим те же самые точки на прямой. Однако если сразу приравнять первую скобку к нулю, то упустим момент смены знака неравенства на противоположенный из-за минуса в этой скобке. Поэтому нужно равносильными переходами упрощать неравенство до того, пока не будет произведение и частное скобок, в каждой из которых линейная функция!
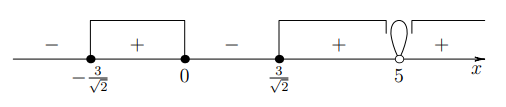
Ответ: \(x \in \left[-\dfrac{3}{\sqrt{2}};\ 0\right] \cup \left[\dfrac{3}{\sqrt{2}};\ 5\right) \cup (5;\ +\infty)\)
Общий алгоритм действия при решение неравенства методом интервалов:
1. Приводим всё к стандартному виду, чтобы справа был ноль
2. Раскладываем всё на произведение или частное множителей
3. Отмечаем все корни на прямой, учитывая выколотые точки и строгость знака неравенства
4. Ставим петельки над теми множителями, которые были в чётных степенях
5. Определяем знак на самом правом промежутке
6. Расставляем дальше знаки справа налево, при этом не меняя знак, переходя через петельки
Задачи для самопроверки
1) \((2x-5)(x+3)\leqslant0\)
2) \(\dfrac{x-2}{3-x}\leqslant0\)
3) \(\dfrac{-14}{x^2+2x-15}\leqslant0\)
4) \(\dfrac{(x+2)(x+1)(x-3)}{(x-4)(x-5)}<0\)
5) \(\dfrac{x^2-6 x+8}{x-1}-\dfrac{x-4}{x^2-3 x+2} \leqslant 0\)
6) \(\dfrac{(x-1)^2(x-2)}{(x-3)}<0\)
7) \(\dfrac{(x-5)^4(x-8)^3}{(x+2)(x-7)^7} \leqslant 0\)
8) \(\dfrac{(x+3) (x+7)^2}{(x+5) (x-2) x^4} \leqslant 0\)
Ответы
1) \(x\in[-3;2,5]\)
2) \(x\in(-\infty;2]\cup(3;+\infty)\)
3) \(x\in(-\infty;-5)\cup(3;+\infty)\)
4) \(x\in(-\infty;-2)\cup(-1;3)\cup(4;5)\)
5) \(x\in(-\infty ;1) \cup(1 ; 2) \cup [3; 4]\)
6) \(x\in(2;3)\)
7) \(x\in(-\infty ;-2) \cup\{5\} \cup(7 ; 8]\)
8) \(x\in(-\infty ;-5) \cup[-3 ; 0) \cup(0 ; 2)\)
