Деление многочленов уголком
Деление многочленов уголком
Давайте вначале вспомним, как мы делим обычные числа уголком. Например, разделим 595 на 17.
Сначала нам от делимого надо отсечь столько разрядов, чтобы полученное число было больше делителя (числа, на которое мы делим). Если мы возьмём 5, то ничего не получится, так как 17 не помещается в 5. Поэтому нужно брать 59. Сколько раз 17 помещается в 59? Результат 3 пишем в частном.
Далее умножаем 3 на 17, полученный результат 51 пишем под числом 59, а далее вычитаем 51 из 59. Получаем 8, а далее сносим следующий разряд - пятёрку. Делим 85 на 17, получаем 5. Умножаем 5 на 17, и результат 85 пишем под числом 85. Вычитаем из верхнего нижнее и получаем ноль.
Значит мы разделили 595 на 17 без остатка и получили 35.

А теперь сделаем те же шаги с многочленами.
Пример 1. Разделим \(x^2+8x+15\) на \(x+5\).
Если при деление чисел мы подразумевали, что делимое больше делителя, то при деление многочленов необходимо, чтобы степень делимого многочлена была больше степени многочлена, на который мы делим. В данном случае мы делим многочлен второй степени на многочлен первой, так что всё в порядке.
Сравниваем старшие элементы многочленов. На что нужно домножить \(x\) у делителя, чтобы получить \(x^2\) у делимого? На ещё один \(x\)! Тогда \(x\) пишем в частное, умножаем его на \(x+5\) и пишем результат под делимым.
Далее нам нужно из \(x^2+8x\) вычесть \(x^2+5x\). Квадраты сокращаются, и получаем результат \(3x\), к которому сносим следующее слагаемое 15. Снова сравниваем старшие коэффициенты многочленов. На что нужно умножить \(x\) у делителя, чтобы получить \(3x\) и делимого? На 3. Тогда в частое пишем +3, умножаем 3 на \(x+5\), пишем результат под делимым.
Тогда получаем, что из \(3x+15\) нужно вычесть \(3x+15\). Получили ноль - значит многочлен \(x^2+8x+15\) разделился на многочлен \(x+5\) без остатка, и в результате получился многочлен \(x+3\).
Тогда мы можем записать это так: \(\dfrac{x^2+8 x+15}{x+5}=x+3\) или же \(x^2+8x+15=(x+5)(x+3).\) Для того, чтобы проверить себя, можно раскрыть скобки и сравнить выражения.
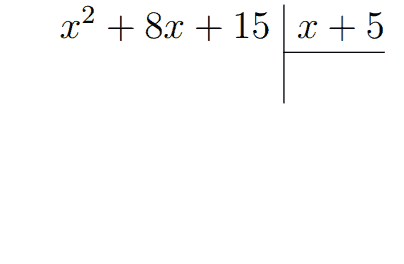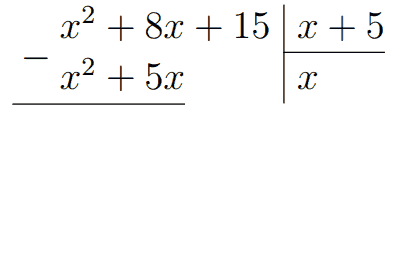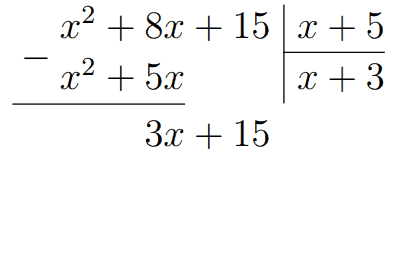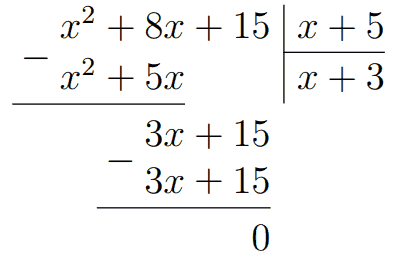
В отличие от деления обычных чисел, нам не нужно выделять определённое количество разрядов, так как мы всегда сравниваем старшие коэффициенты многочленов.
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Рассмотрим ещё один пример.
Пример 2. \(\dfrac{x^2+x-2}{x-1}\).
Сравниваем старшие коэффициенты: \(x^2\) и \(x\). На что нужно умножить второе, чтобы получить первое? Очевидно, что на \(x\). Умножаем \(x\) на \(x-1\), пишем результат под делимым и вычитаем полученный результат из него. \(x^2-x^2=0\), и \(x-(-x)=2x\). Обратите внимание, что мы вычитаем отрицательное число, поэтому, при раскрытие скобок, знак станет плюсом.
Спускаем следующее слагаемое и получаем \(2x-2\). Сравниваем старшие коэффициенты и понимаем, что для того, чтобы из \(x\) получить \(2x\), надо первое умножить на 2. Умножаем 2 на \(x-1\), получаем \(2x-2\) и вычитаем из \(2x-2\). Мы получили ноль, а значит деление закончено без остатка, и результатом стал многочлен \(x+2\).

Пример 3. \(\dfrac{x^3+2 x^2-9 x-18}{x+3}\).
Сравниваем старшие коэффициенты. Для того, чтобы получить \(x^3\), надо \(x\) из делителя умножить на \(x^2\), значит он идёт в частное. Далее умножаем \(x^2\) на \(x+3\), результат \(x^3+3x^2\) пишем под \(x^3+2x^2\) и производим вычитание.
Далее к получившемуся \(-x^2\) спускаем \(-9x\). Чтобы получить \(-x^2\), надо \(x\) из делителя умножить на \(-x\), тогда в частном пишем \(-x\). Умножаем \(-x\) на \(x+3\), и результат \(-x^2-3x\) вычитаем из \(-x^2-9x\), тем самым получаем \(-6x\), ведь \(-x^2-(-x^2)=0\) и \(-9x-(-3x)=-6x\). Спускаем -18.
Наконец делим \(-6x-18\) на \(x+3\). Для этого нужно \(x+3\) умножить на -6. После вычитания получаем ноль и итоговый ответ: \(x^2-x-6\).

Пример 4. \(\dfrac{x^3+3 x^2+50}{x+5}\).
Особенность этого примера в том, что у делимого отсутствует \(x\). Но для удобства деления нужно дописать коэффициент перед ним. То есть делимое примет вид: \(x^3+3x^2+0x+50\). А теперь уже начинаем деление.
Сравниваем \(x^3\) и \(x\): нужно умножить на \(x^2\), пишем его в частное. После умножения и вычитания получаем \(-2x^2\), к которому спускаем \(0x\). Чтобы из \(x\) получить \(-2x^2\), нужно первое умножить на \(-2x\). Пишем его в частное, а под \(-2x^2+0x\) пишем \(-2x^2-10x\).
После вычитания получается \(10x\), и также сносим +50. Далее нужно умножить \(x+5\) на 10, чтобы из \(x\) получит \(10x\). Тогда +10 идёт в частное, а остаток от деления получается равным нулю. Ответ: \(x^2-2x+10\).
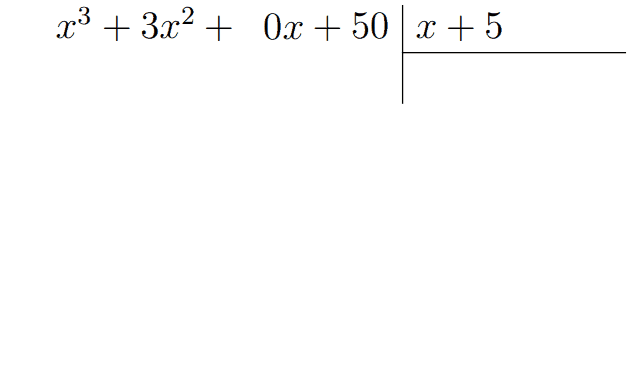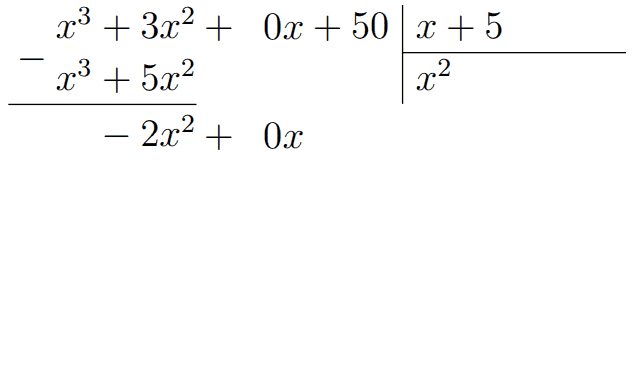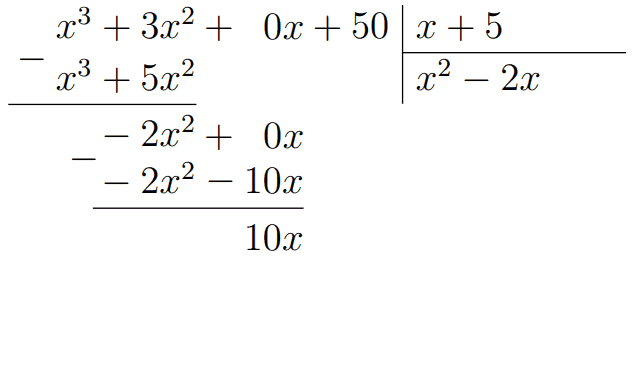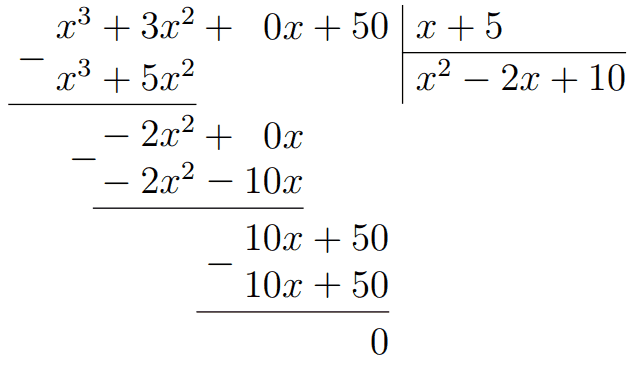
Пример 5. Найдём остаток от деления \(x^5-5 x^4-3 x^3+4 x^2+2 x-8\) на \(x+1\).
Действуем по прежнему алгоритму. Чтобы получить \(x^5\), нужно \(x\) умножить на \(x^4\), его пишем в частное. Далее из \(x^5-5x^4\) вычитаем \(x^4\cdot(x+1)=x^5+x^4\) и получаем \(-6x^4\). Спускаем \(-3x^3\).
Для того, чтобы получить \(-6x^4\), нужно \(x\) умножить на \(-6x^3\), его пишем в частное. Далее из \(-6x^4-3x^3\) вычитаем \(-6x^3\cdot(x+1)=-6x^4-6x^3\) и получаем \(3x^3\). Спускаем \(4x^2\).
Для того, чтобы получить \(3x^3\), нужно \(x\) умножить на \(3x^2\), его пишем в частное. Далее из \(3x^3+4x^2\) вычитаем \(3x^2\cdot(x+1)=3x^3+3x^2\) и получаем \(x^2\). Спускаем \(2x\).
Для того, чтобы получит \(x^2\), нужно \(x\) умножить на \(x\), его пишем в частное. Далее из \(x^2+2x\) вычитаем \(x\cdot(x+1)=x^2+x\) и получаем \(x\). Спускаем -8.
И наконец, чтобы получить \(x\), нужно \(x\) умножить на 1, её пишем в частное. И далее из \(x-8\) вычитаем \(1\cdot(x+1)=x+1\) и получаем \(-9\).
Так как теперь степень делимого (равная нулю) стала меньше степени делителя (равной единице), то дальнейшее деление невозможно. А так как мы получили не ноль, значит, что \(x^5-5 x^4-3 x^3+4 x^2+2 x-8\) нацело не делится на \(x+1\), а только с остатком, равным -9.
Тогда верна следующая запись: \(x^5-5 x^4-3 x^3+4 x^2+2 x-8=\) \((x+1)(x^4-6x^3+3x^2+x+1)-9\). Можно раскрыть скобки, привести подобные слагаемые и проверить себя.

Теперь разберём случай, когда мы делим на многочлен второй степени.
Пример 6. Разделим \(2 x^4-10 x^3+23 x^2-22 x-3\) на \(x^2-3 x+5\).
Здесь, как и всегда, сравниваем старшие степени. Чтобы получить \(2x^4\), нужно \(x^2\) умножить на \(2x^2\), значит оно идёт в частное. Далее умножаем \(2x^2\) на \(x^2-3x+5\) и вычитаем из \(2x^2-10x^3+23x^2\), получаем \(-4x^3+13x^2\).
Далее действуем аналогично. В итоге мы получим, что у нас остаётся \(x-8\), но оно никак не разделится на \(x^2-3x+5\), так как степень делимого меньше степени делителя. Значит, это остаток.
Тогда можно записать, что \(2 x^4-10 x^3+23 x^2-22 x-3=\) \((x^2-3x+5)(2x^2-4x+1)+(x-8)\) или \(\dfrac{2 x^4-10 x^3+23 x^2-22 x-3}{x^2-3 x+5}=\) \(2 x^2-4 x+1+\dfrac{x-8}{x^2-3 x+5}\).

Если перед нами стоит задача решить равнение степени больше, чем 2, и при этом не получается разложить на множители методом группировки, то алгоритм такой. Первым делом записываем многочлен в стандартном виде, то есть необходимо, чтобы степени шли в порядке убывания. Дальше подбором находим один из корней многочлена. Корень многочлена - это все возможные делители свободного члена (а если коэффициент перед старшей степенью не равен единице, то все возможные делители образуются как частное свободного члена и старшего коэффициента).
Пример 7. Например, нужно решить уравнение \(6x^2+6+x^3+11x=0\).
Вначале перепишем его в правильном порядке: \(x^3+6x^2+11x+6\). Корнями уравнения могут быть делители числа 6, то есть это числа \(\pm1, \pm2, \pm3, \pm6\). Если мы перед \(x^3\) стояло, например, число 2, то тогда к этим восьми делителям добавились бы ещё восемь, у которых в знаменателе стоит эта самая двойка. Подставляя поочерёдно числа в уравнение, получаем, что \(x=-1\) подходит, потому что \((-1)^3+6(-1)^2+11(-1)+6=\) \(-1+6-11+6=0\). А нам как раз нужно, чтобы при подстановке нужного числа в результате получился ноль.
Значит, многочлен \(x^3+6x^2+11x+6\) нацело делится на \(x+1\), ведь \(x=-1\) - его корень. В общем виде нам нужно поделить исходный многочлен на \(x-x_0\), где \(x_0\) - найденный корень. Тогда мы в столбик производим это самое деление.
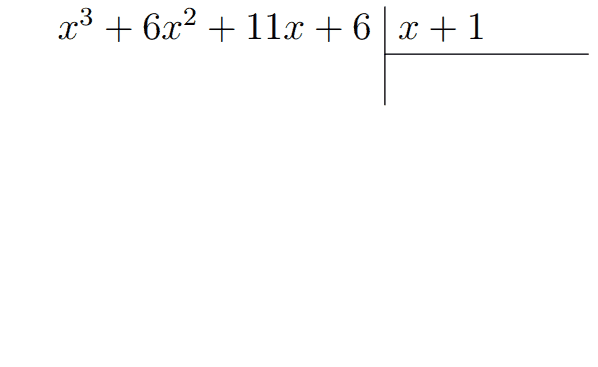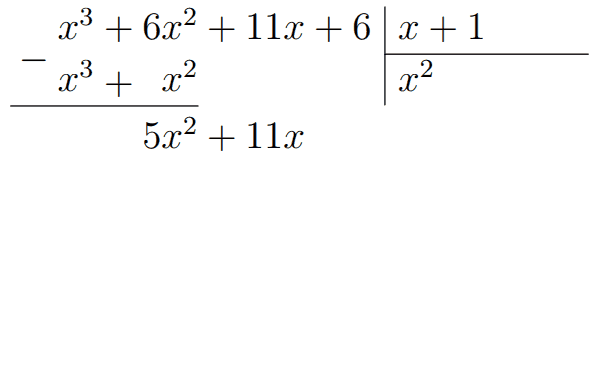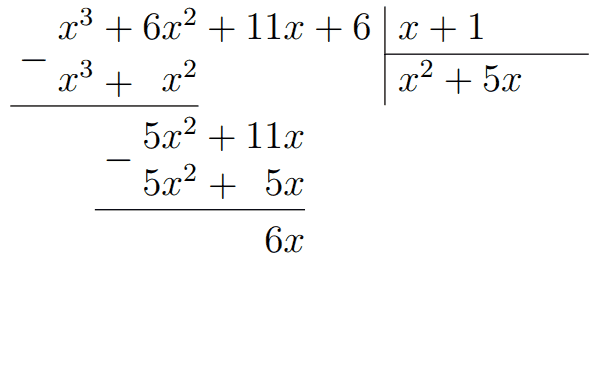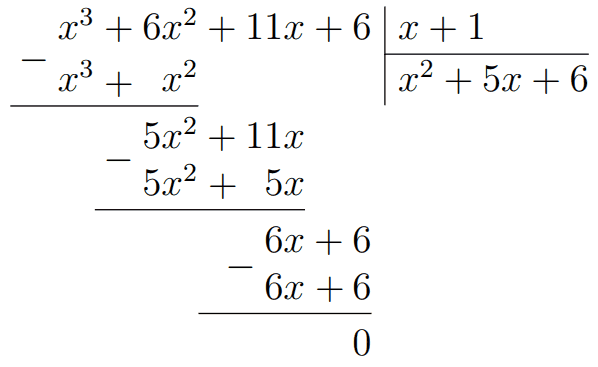
В результате мы получили многочлен \(x^2+5x+6\). То есть \(x^3+6x^2+11x+6=\) \((x+1)(x^2+5x+6)\). Если есть сомнения в правильности разложения, то можно проверить его раскрытием скобок. В результате раскрытия \((x+1)(x^2+5x+6)\) должен получится исходный многочлен.
Если в результате деления столбиком получился не ноль, значит, в решение есть ошибка: или неверно подобран корень уравнения, или ошибка в процессе деления уголком.
Получившееся квадратное уравнение легко раскладывается на множители. Тогда итоговый результат таков: \(x^3+6x^2+11x+6=\) ((x+1)(x+2)(x+3)\). И теперь решение уравнения очевидно.
Пример 8. Задача посложнее: решим неравенство \(x^4-3x^3+6x-4\geqslant0\).
Первым делом нужно разложить многочлен \(x^4-3x^3+6x-4\) на множители. Среди чисел \(\pm1, \pm2, \pm4\) находим, что при \(x=1\) многочлен обращается в ноль. Тогда поделим \(x^4-3x^3+6x-4\) на \(x-1\), не забыв дописать слагаемое \(0x^2\).

Теперь наш многочлен принял такой вид: \((x-1)(x^3-2 x^2-2 x+4)\). Нужно разложить вторую скобку. Здесь можно действовать через деление уголком, а можно просто воспользоваться группировкой: \(x^3-2x^2-2x+4=\) \(x^2(x-2)-2(x-2)=\) \((x-2)(x^2-2)=\) \((x-2)(x-\sqrt{2})(x+\sqrt{2})\).
Тогда с помощью метода интервалов решаем неравенство \((x-1)(x-2)(x-\sqrt{2})(x+\sqrt{2})\geqslant0\).

Получаем ответ \(x\in(-\infty ;-\sqrt{2}] \cup[1 ; \sqrt{2}] \cup[2 ; +\infty)\).
А подробнее про метод интервалов можно почитать здесь.
Алгоритм деления многочленов уголком (в столбик)
1. Записать многочлен в стандартном виде, то есть необходимо, чтобы степени шли в порядке убывания
2. Если в исходном многочлене пропущены какие-то степени, то их нужно добавить, но с нулевыми коэффициентами
3. Всегда сравнивать старшую степень делимого со старшей степенью делителя и повторять это на каждом шагу
Задачи для самопроверки
Выделить целуя часть дроби и найти остаток от деления
1) \(\dfrac{8t^2+10t-3}{2t+3}\)
2) \(\dfrac{x^3+5x^2-2x-6}{x+1}\)
3) \(\dfrac{4x^2+7x-3}{x-2}\)
4) \(\dfrac{x^3-2x^2+7x-3}{x^2+1}\)
5) \(\dfrac{x^5+5x^3+6}{x^2+2x+3}\)
Решить уравнение
6) \(x^4+4x^3-18x^2-12x+9=0\)
7) \(x^4-4 x^3-19 x^2+106 x-120=0\)
Ответы
1) \(4t-1; 0\)
2) \(x^2+4x-6; 0\)
3) \(4x+15 ; 27\)
4) \(x-2 ; 6x-1\)
5) \(x^3-2x^2+6x-6; -6x+24\)
6) \(-1; 3; -3\pm2\sqrt2\)
7) \(-5; 2; 3; 4\)
