Векторы ЕГЭ профильная математика. 2 задание

Как найти вектор

1 способ. Чтобы найти вектор, нужно из координат начала вычесть координаты конца.

Начало вектора \(\vec{a}\) имеет координаты (1; 2), конец вектора координаты (3; 3). Тогда \(\vec{a}=(3-1;3-2)=(2;1)\)

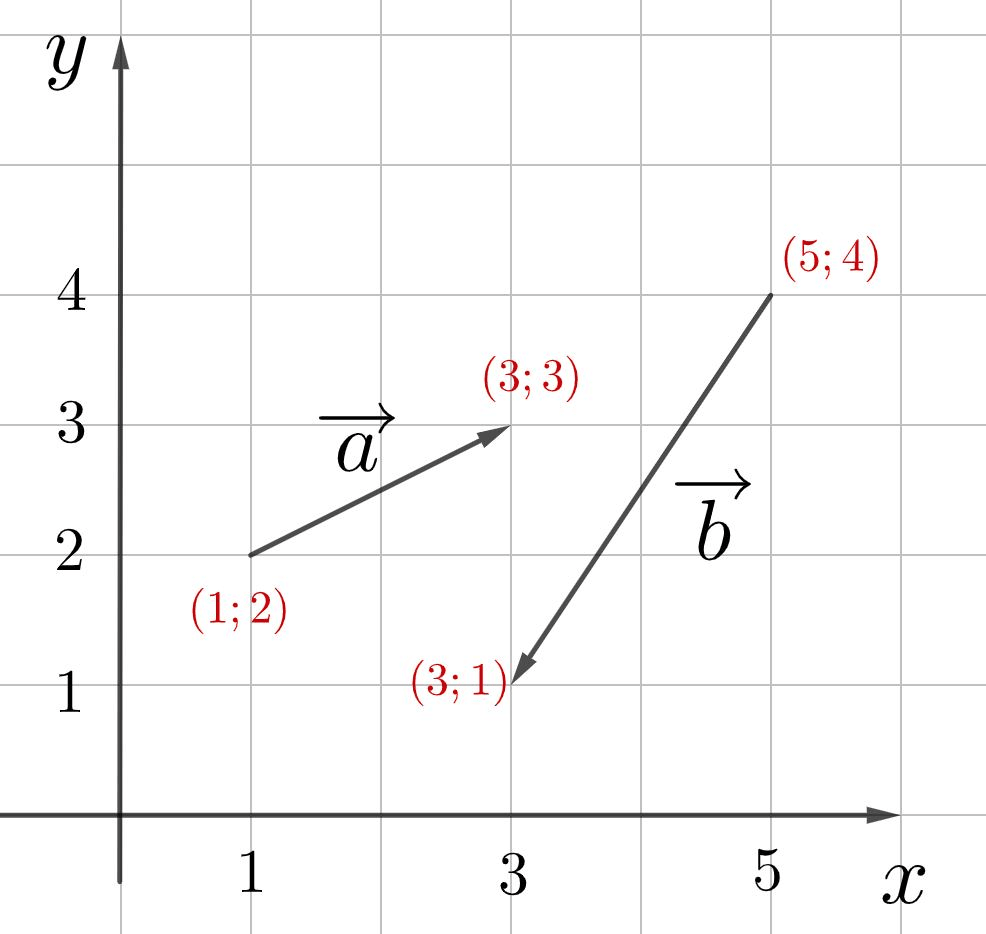
 2 способ. По рисунку можно сделать гораздо проще: из начала вектора \(\vec{a}\) идете к его концу сначала вдоль оси \(x\), потом вдоль оси \(y\).

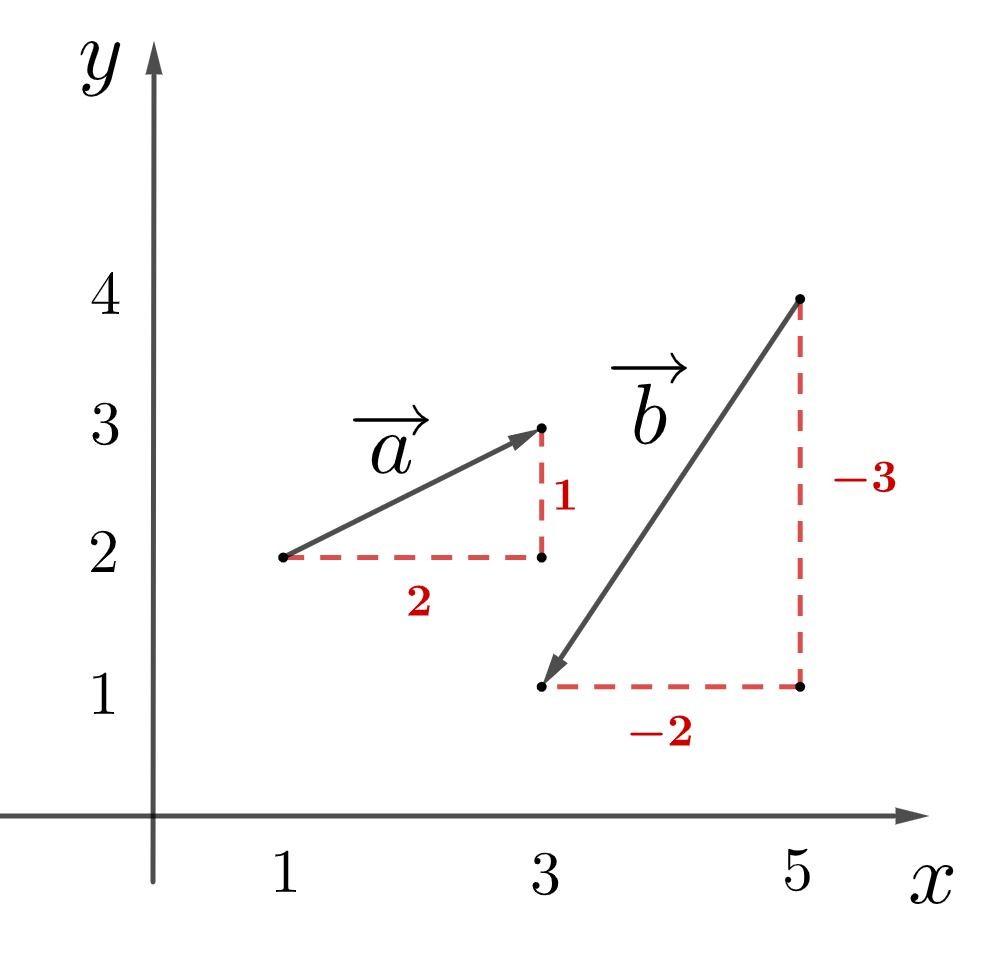
Чтобы из начала вектора \(\vec{a}\) дойти до конца, нужно по направлению оси \(x\) пройти 2 клетки и по направлению оси \(y\) одну клетку, поэтому  \(\vec{a}=(2;1)\)

Чтобы найти вектор \(\vec{b}\), нужно 2 клетки пройти против оси \(x\) и против оси \(y\) пройти 3 клетки, поэтому \(\vec{b}= (-2; -3)\)

Не путайте начало и конец вектора! Конец вектора - это где стрелка.

Стратегия подготовки к ЕГЭ по профильной математике https://marseltutor.ru/

Как найти длину вектора

Если \(\vec{a}=(x; y)\), то \(|\vec{a}|=\sqrt{x^2+y^2}\)

Например: \(\vec{a}=(3 ;-4)\), тогда \(|\vec{a}|=\sqrt{3^2+(-4)^2}=\sqrt{9+16}=\sqrt{25}=5\)

Как найти скалярное произведение векторов

Если \(\vec{a}=\left(x_1; y_2\right)\) и \(\vec{b}=\left(x_2; y_2\right)\), то \(\vec{a} \cdot \vec{b}=x_1 \cdot x_2+y_1 \cdot y_2\)

Например: \(\vec{a}=(3 ; 7)\) и \(\vec{b}=(-1 ; 4)\), тогда \(\vec{a} \cdot \vec{b}=3 \cdot(-1)+7 \cdot 4=-3+28=25\)

Как найти скалярное произведение, если в условии есть угол между векторами

\(\vec{a} \cdot \vec{b}=|\vec{a}| \cdot|\vec{b}| \cdot \cos \alpha\)

Например, длины векторов \(\vec{a}\) и \(\vec{b}\) равны 3 и 7 , а угол между ними равен \(60^{\circ}\). Нужно найти скалярное произведение \(\vec{a} \cdot \vec{b}\).

\(\vec{a} \cdot \vec{b}=3 \cdot 7 \cdot \cos 60=21 \cdot \dfrac{1}{2}=10,5\)

Значения косинусов, которые могут понадобиться

\(\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}\)

\(\cos 45^{\circ}=\dfrac{\sqrt{2}}{2}\)

\(\cos 60^{\circ}=\dfrac{1}{2}\)

Как найти угол между векторами

\(\cos \alpha=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}\)

Например: \(\vec{a}=(-3 ; 4)\) и \(\vec{b}=(5 ; -12)\), тогда \(|\vec{a}|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5\) и \(|\vec{b}|=\sqrt{5^2+(-12)^2}=\sqrt{25+144}=\sqrt{169}=13\). 

И далее \(\cos \alpha=\dfrac{-3\cdot5+4\cdot (-12)}{5\cdot 13}=\dfrac{-15-48}{65}=-\dfrac{63}{65}\)