☀️
🌙
2. Векторы
Чтобы получить дополнительный функционал нужно войти.
194
Даны векторы \(\vec{a}(-13 ; 4)\) и \(\vec{b}(-6 ; 1)\). Найдите скалярное произведение \(\vec{a} \cdot \vec{b}\).
Ответ
82
195
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите длину вектора \(\vec{a}+4 \vec{b}\).
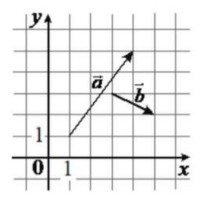
Ответ
11
196
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координатами которых являются целые числа. Найдите скалярное произведение \(\vec{a} \cdot \vec{b}\)
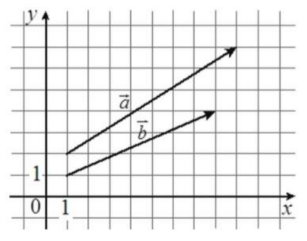
Ответ
71
197
Длины векторов \(\vec{a}\) и \(\vec{b}\) равны 3 и 5 , а угол между ними равен \(60^{\circ}\). Найдите скалярное произведение \(\vec{a} \cdot \vec{b}\).
Ответ
7,5
198
Даны векторы \(\vec{a}(1 ; 2), \vec{b}(-3 ; 6)\) и \(\vec{c}(4 ;-2)\). Найдите длину вектора \(\vec{a}-\vec{b}+\vec{c}\).
Ответ
10
199
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение \(\vec{a} \cdot \vec{b}\).
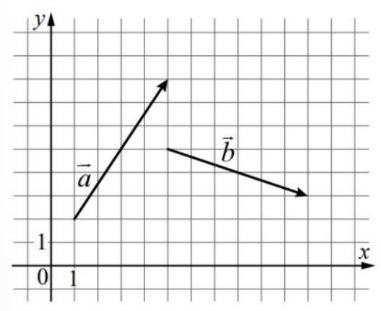
Ответ
12
