11 задание ЕГЭ профиль. Графики функций
11 задание ЕГЭ профильная математика. Теория по графикам
Прямая y=kx+b
\(y=kx+b\) - прямая. Коэффициент \(b\) - точка пересечения оси \(y\)
Например, \(y=x+3\) пересекает ось \(y\) в точке 3, поэтому \(b=3\)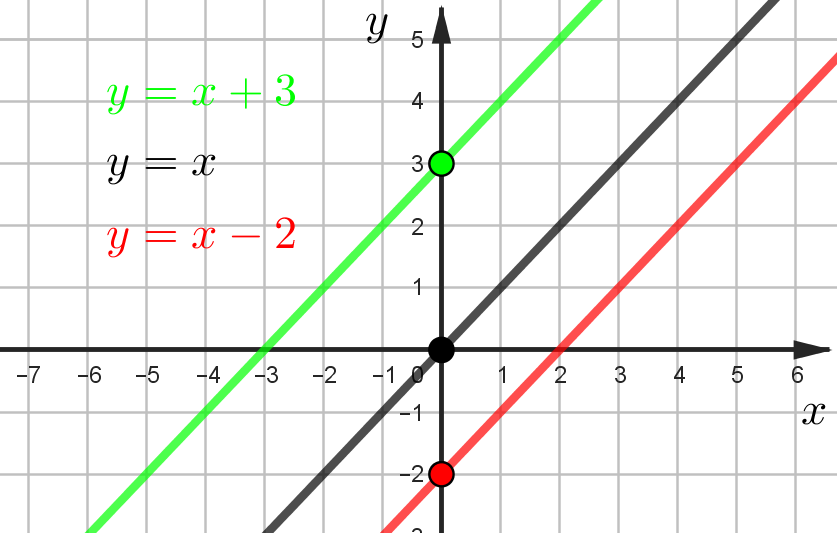
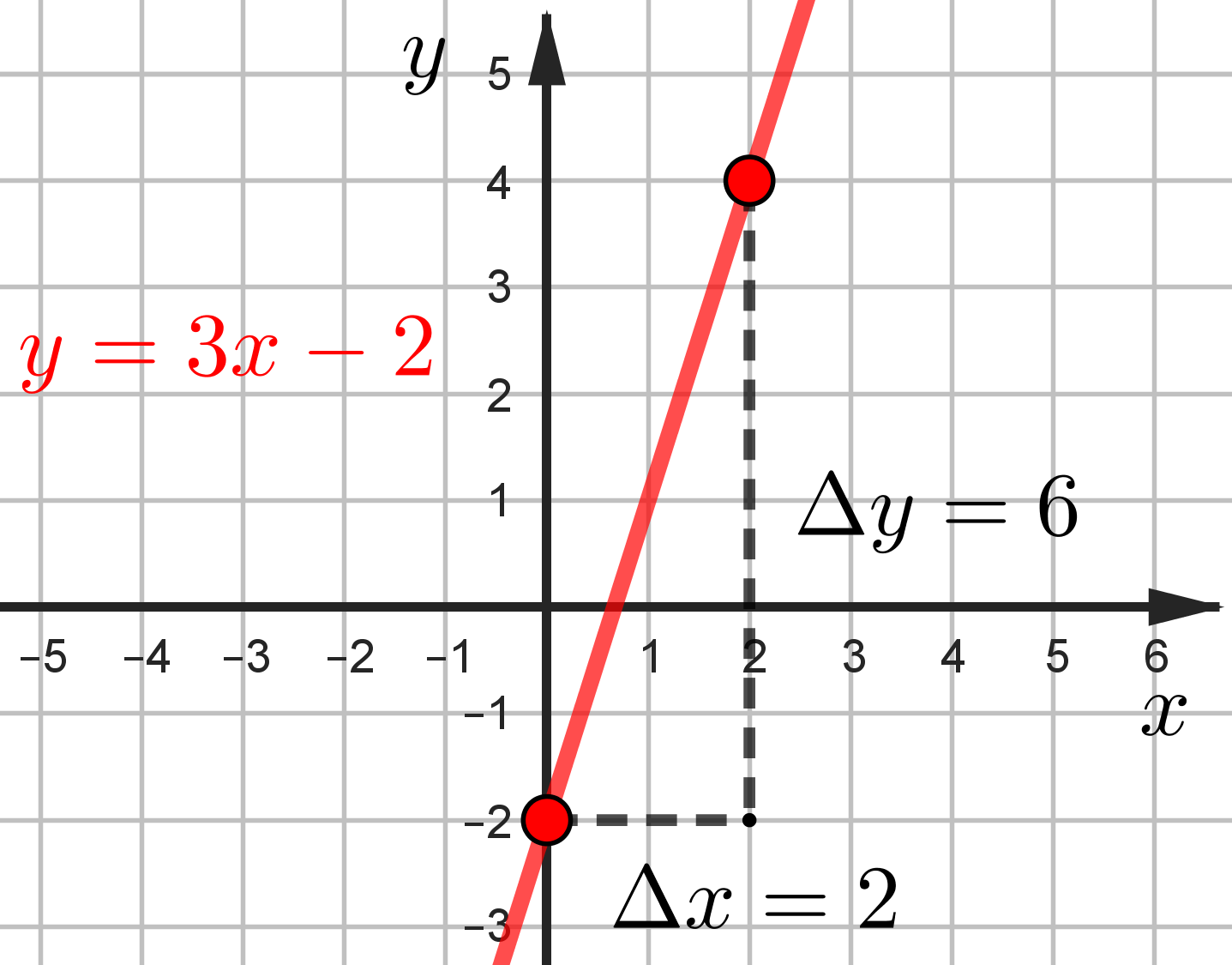
Чтобы найти коэффициент \(k\) нужно выбрать две точки с целочисленными координатами. Из левой точки (0; -2) пойти горизонтельно вправо, пока не поравняешься со второй точкой по вертикали. Потом вертикально подняться (\(k>0)\) или спуститься \((k<0)\)
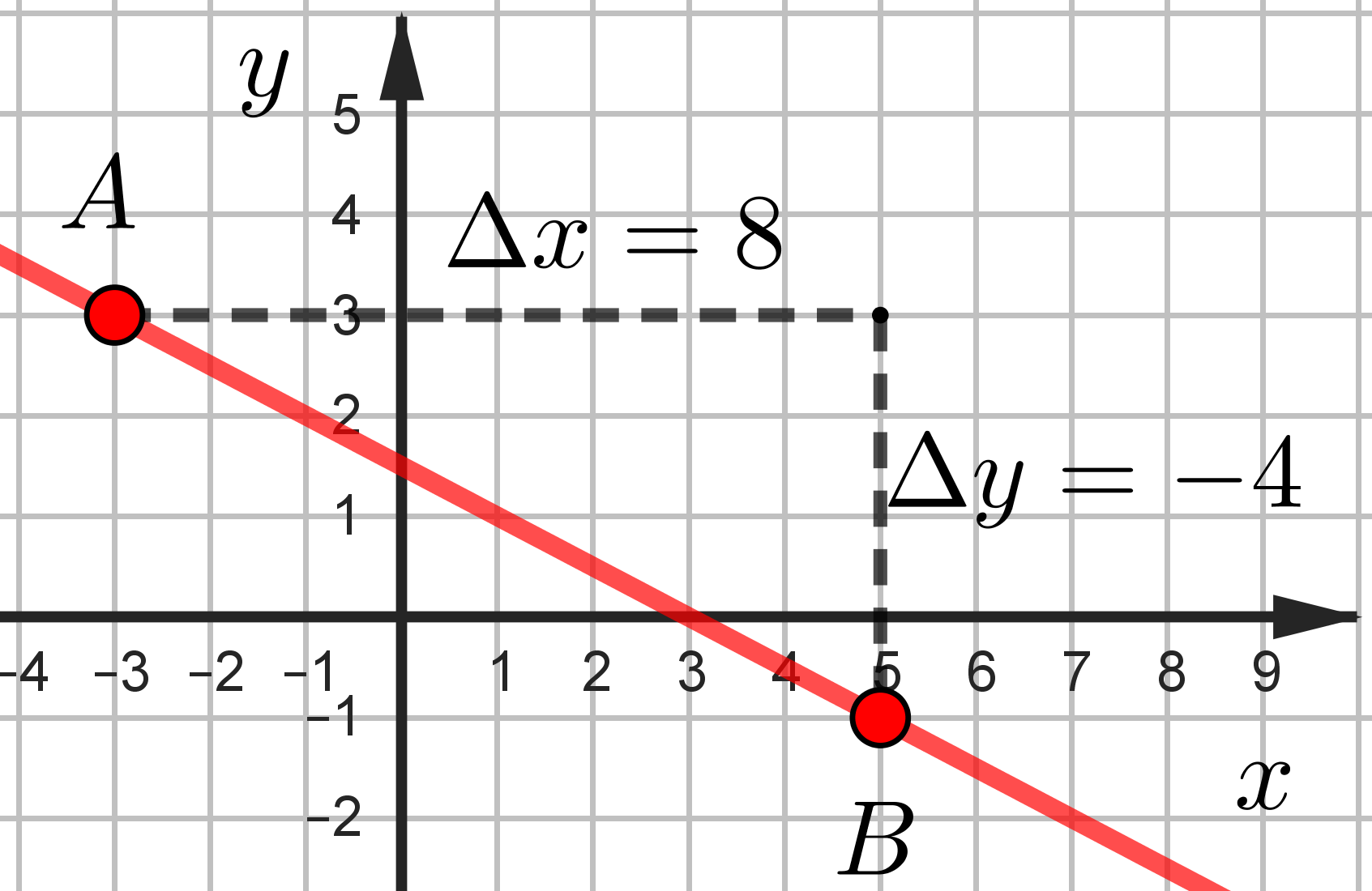
Если по графику непонятно, где прямая пересекает ось \(y\), сначала находим коэффицент \(k\). Обратите внимание, что от точки \(A\) мы сначала идем горизонтально вправо и дальше вертикально вниз, поэтому \(k<0\).
Получаем \(y=-\dfrac{4}{8}x+b\). После этого подставляем любую координату, например, \((5; -1)\) и решаем уравнение \(-1=-0,5\cdot 5+b\), чтобы найти \(b\)
Парабола
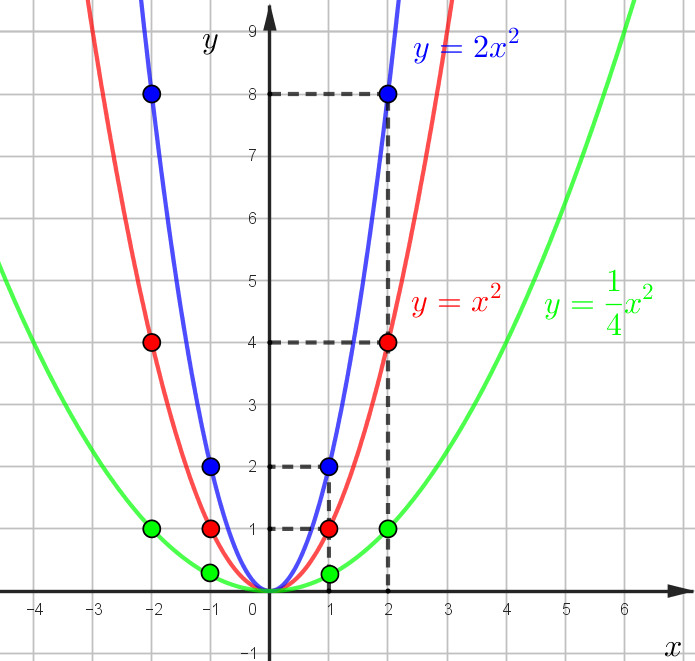
\(y=x^2\) - красный график. Назовем его "Эталон". Ключевые точки (1;1), (2;4), (3;9)
\(y=2x^2\) синий график. Каждое значение \(y\) в 2 раза больше эталона. (1;2), (2;8), (3;18)
\(y=\dfrac{1}{4}x^2\) -зеленый график. Каждое значение \(y\) в 4 раза меньше эталона. (1;1/4), (2;1), (3;9/4)
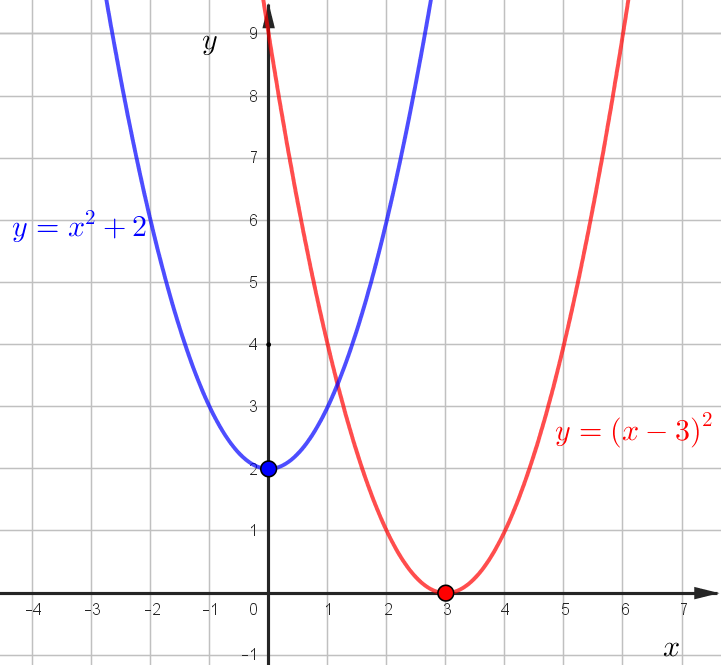
\(y=x^2+c\) - график "эталон" \(y=x^2\) поднимается на \(c\) клеток вверх. Например, \(y=x^2+2\).
\(y=(x+b)^2\) - график "эталон" \(y=x^2\) смещается по горизонтали на \(b\), если \(b<0\) - вправо, \(b>0\) - влево. Например, \(y=(x-3)^2\) - график смещается вправо на 3.
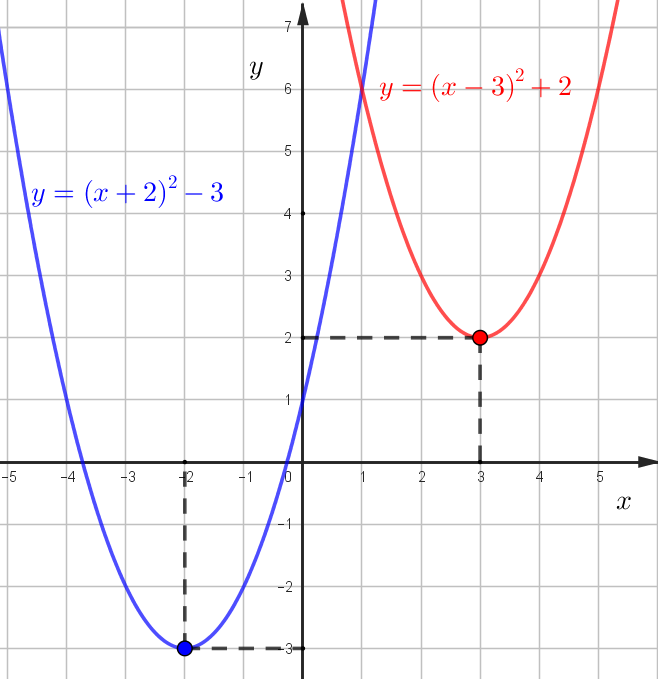
\(y=(x+b)^2+c\).
\(-b\) - вершина параболы по оси \(x\),
\(c\) - вершина параболы по оси \(y\).
Например, \(y=(x+2)^2-3\). Вершина параболы имеет координаты (-2; -3)
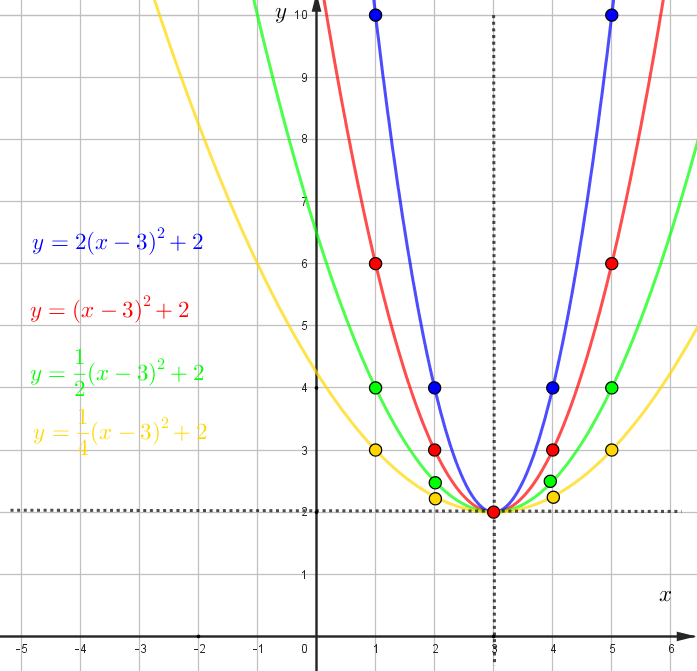
\(y=a(x+b)^2+c\). Чтобы определить \(a\) проводите пунктирные линии, как на рисунке. Теперь отходим от вершины параболы на 1
вправо и смотрим на сколько изменился \(y\). Если на 1, то a=1, если на 2, то \(a=2\), если на 0,5, то \(a=0,5\)
Если ветви параболы направлены вниз, \(a<0\). Отходим от вершины вправо на 1, смотрим, как изменился \(y\). Отошли вправо на 1,
(y\) - уменьшился на 2, значит \(a=-2\)
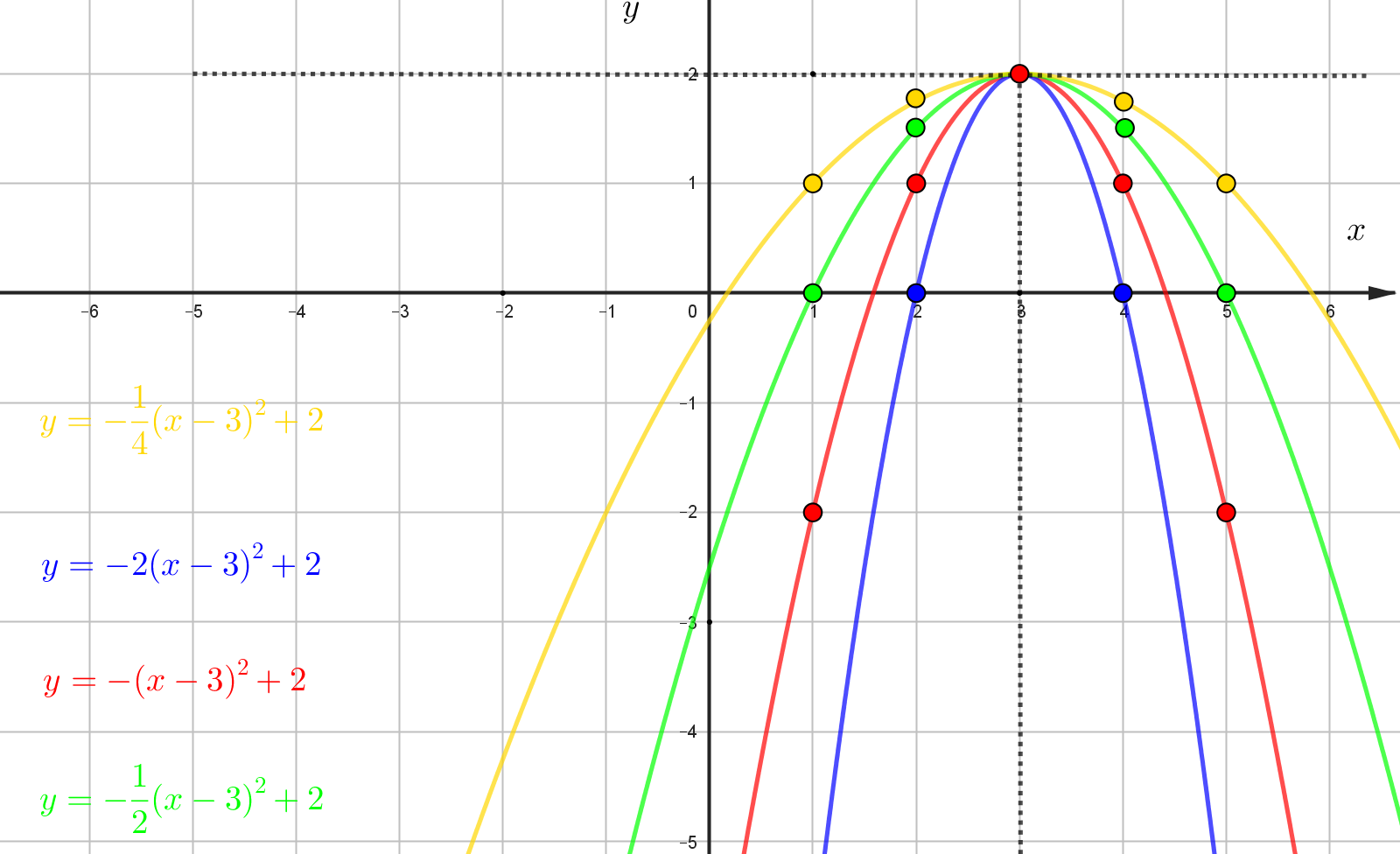
Не путайте \(y=ax^2+bx+c\) и \(y=a(x-b)^2+c\). В каждой функции \(b\) и \(c\) это разные коэффиценты
Если по графику не видно, где находится вершина параболы, то пробуем найти коэффициент \(c\) - точка пересечения оси \(y\).
Выбираем две точки через которые проходит парабола и составляем систему. Например, можно выбрать точки (1;1) и (-4;1).

Все шпаргалки и теория ЕГЭ по профильной математике в ТЕЛЕГРАМ
Гипербола
\(y=\dfrac{k}{x}\) - гипербола. Чтобы определить коэффициент \(k\), посмотрите, чему равно значение \(y\), когда \(x=1\). Или можно
подставить значения любой точки, которая принадлежит графику
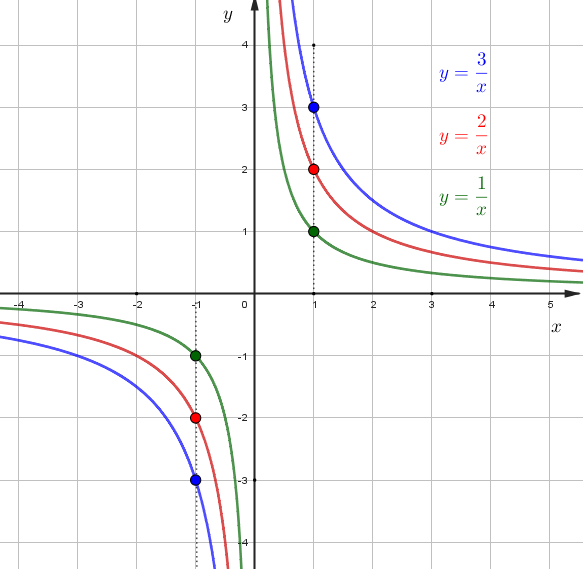
Если \(k<0\), то гипербола находится во 2 и 4 четверти.
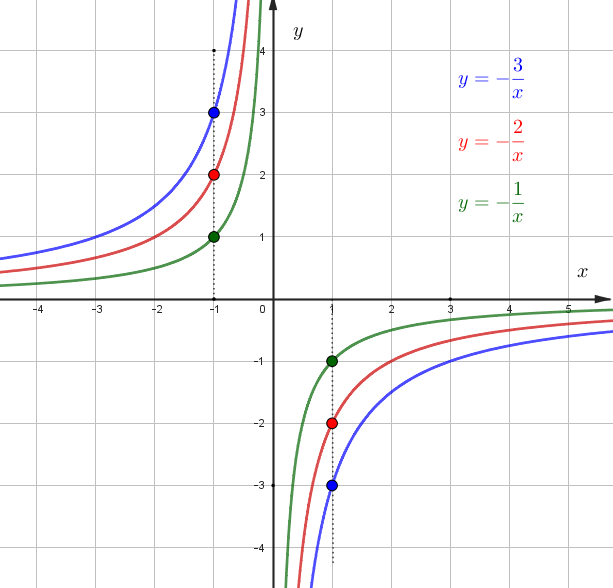
\(y=\dfrac{k}{x}+c\),
\(c\) - подъем/спуск гиперболы. Для удобства проведите асимптоту
Например, \(y=\dfrac{2}{x}+3\), \(c=3\) - это \(y=\dfrac{2}{x}\) которую подняли вверх на 3 единицы (асимптота проходит через точку \(y=3\))
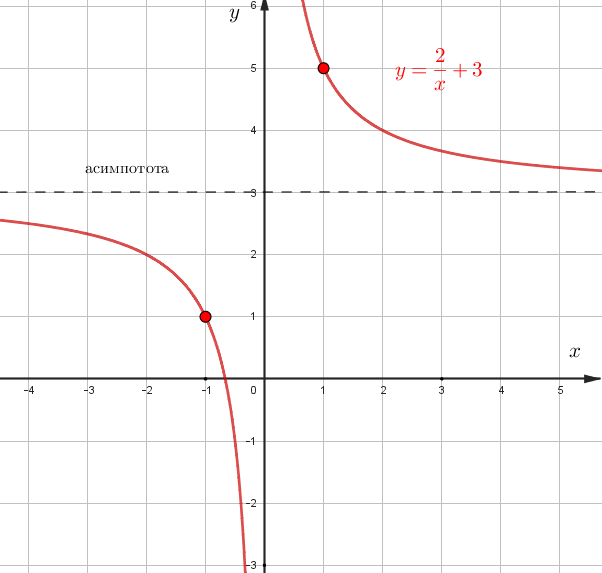
\(y=\dfrac{k}{x+b}\), \(b\) - сдвиг гиперболы вправо/влево.
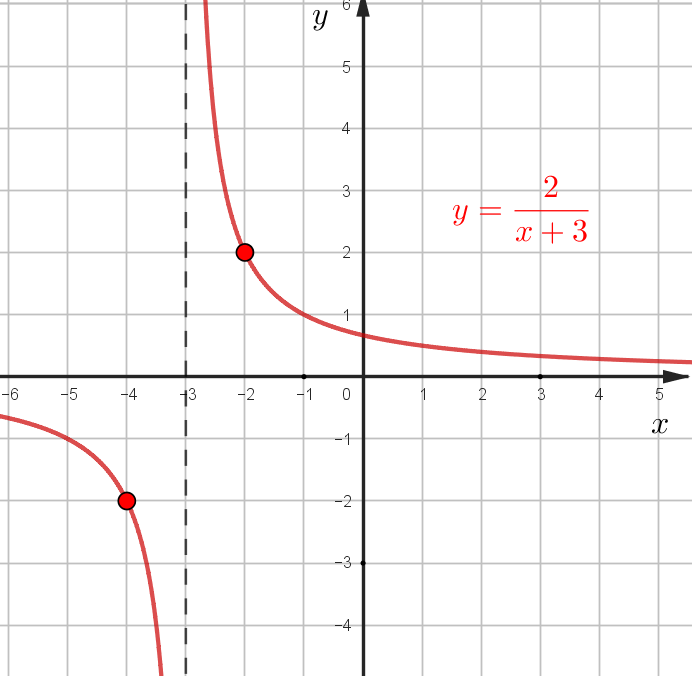
Например, \(y=\dfrac{2}{x+3}\), это \(y=\dfrac{2}{x}\), который сдвинули на 3 влево. \(b<0\) - вправо, \(b>0\) - влево
\(y=\dfrac{k}{x+b}+c\),
\(b\) - сдвиг вправо/влево, \(c\) - спуск/подъем. Для удобства проводите асимптот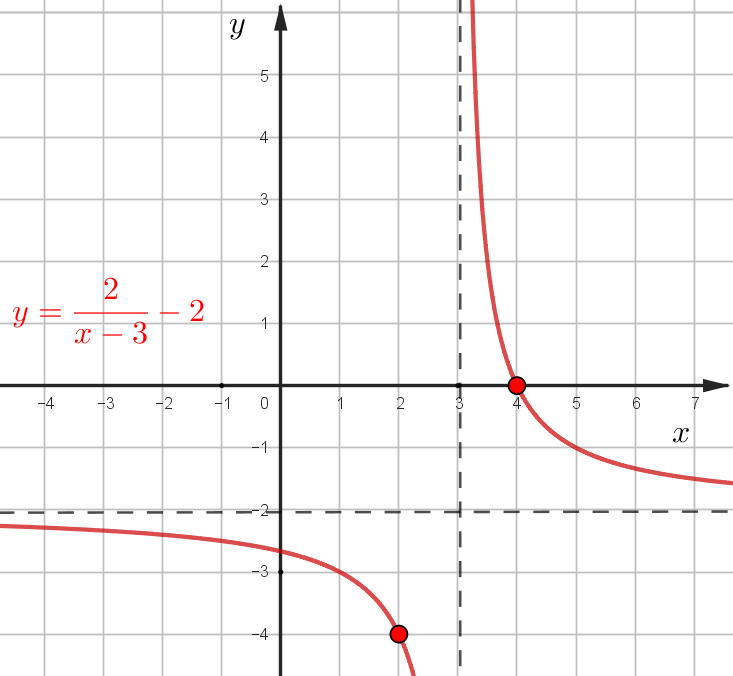
Пример: серия гипербол \(b=3\), \(c=-2\). Как быстро определить \(k\). Прерывистые линии представьте новыми осями координат.
Посмотрите на цветные точки, если вправо отойти на 1 от точки пересечения асимпотот. Желтая: (1;1), значит \(k=1\), красная (1;2), значит \(k=2\)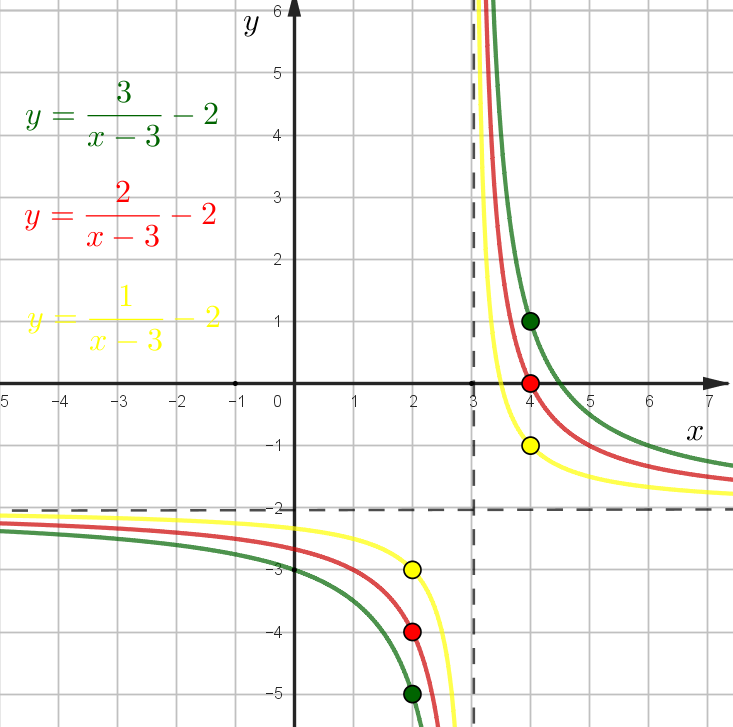
Если коэффициент \(k<0\)
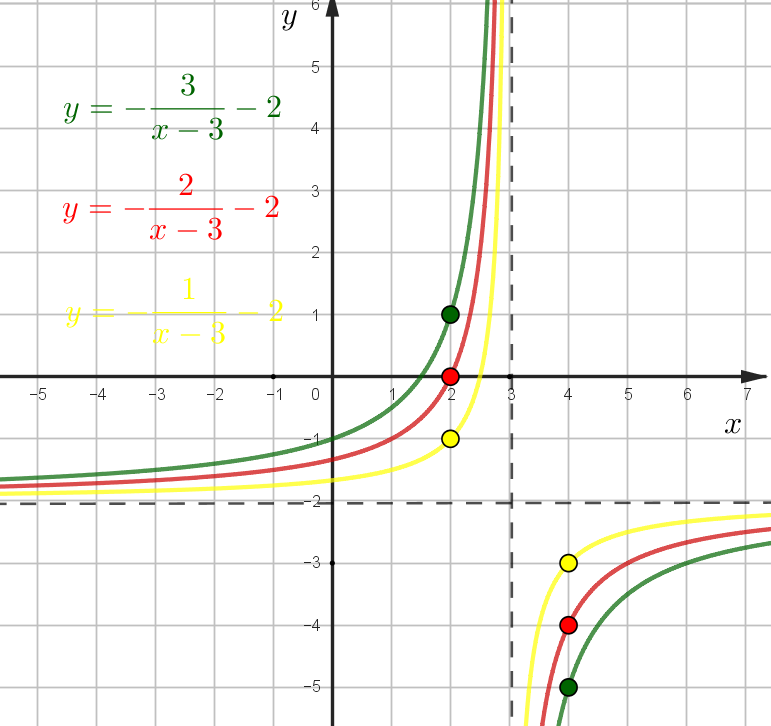
Бесплатные уроки по 11 заданию ЕГЭ в ТЕЛЕГРАММ
График логарифма
\(y=\log_a x\). График при всех значениях \(a>0\) проходит через точку (1;0),
\(a>1\) - функция возрастающая, \(0<a<1\) - убывающая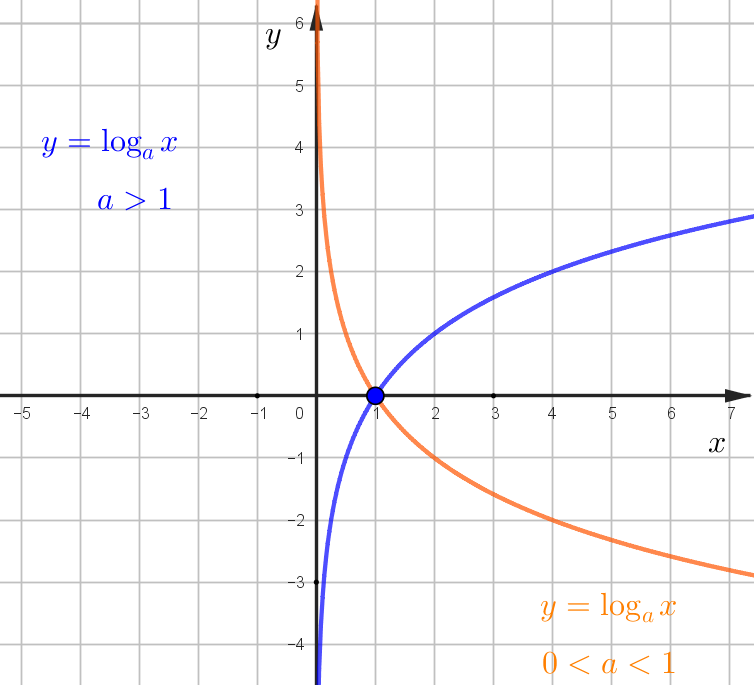
\(y=\log_a(x+b)\), \(b\) - сдвиг вправо/влево.
Например, \(y=\log_a(x+3)\). График \(y=\log_a x\) всегда пересекает ось \(x\) в точке 1, значит при \(b=-3\) сдвиг точки пересечения
оси \(x\) на 3, то есть в точке -2
\(y=\log_a x+c\) - подъем/спуск.
Например, \(y=\log_a x+3\) Смотрим, чему равно значение \(y\) при \(x=1\). Значение \(y\) и будет равно 3, поэтому \(c=3\)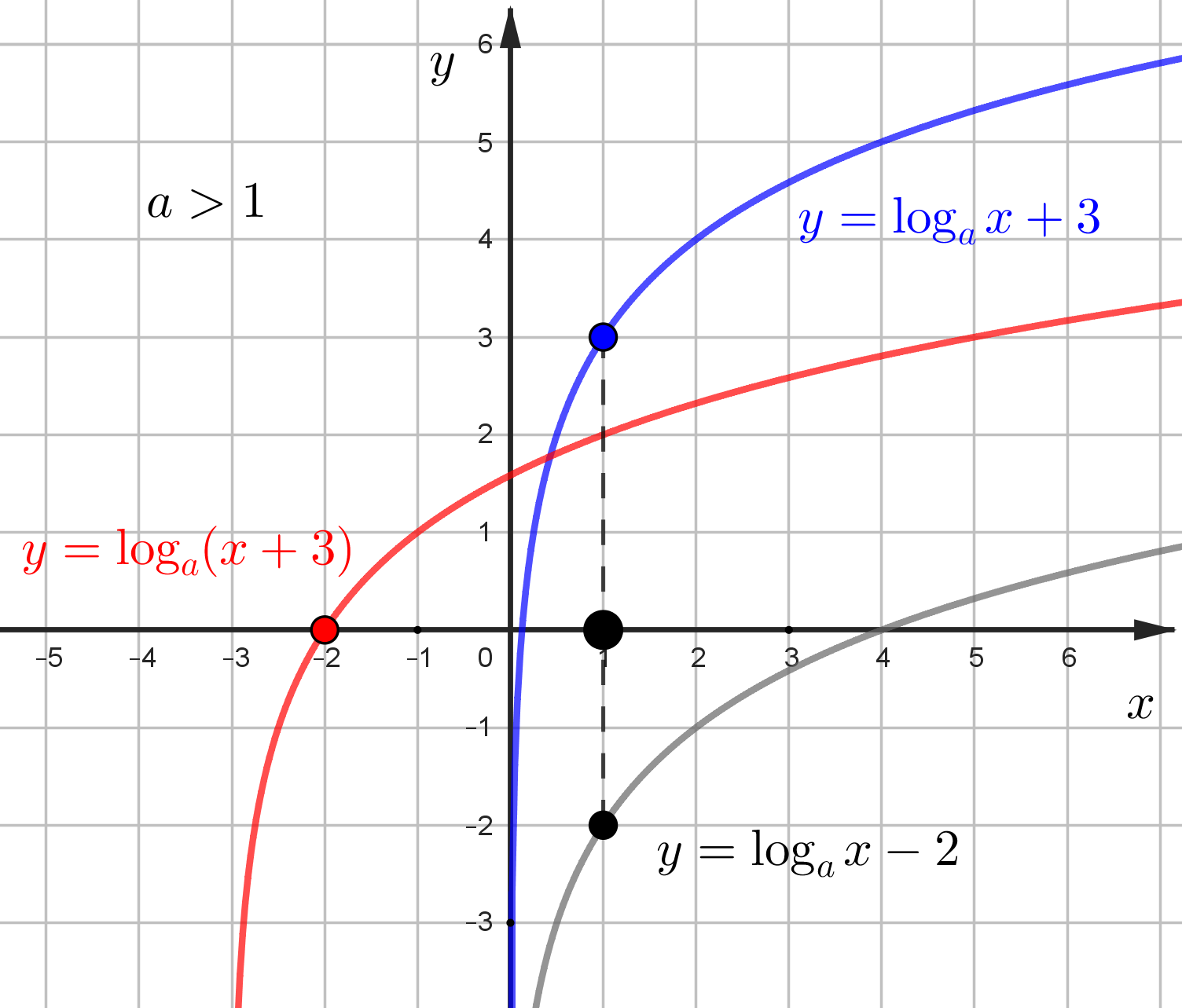
При \(0<a<1\)
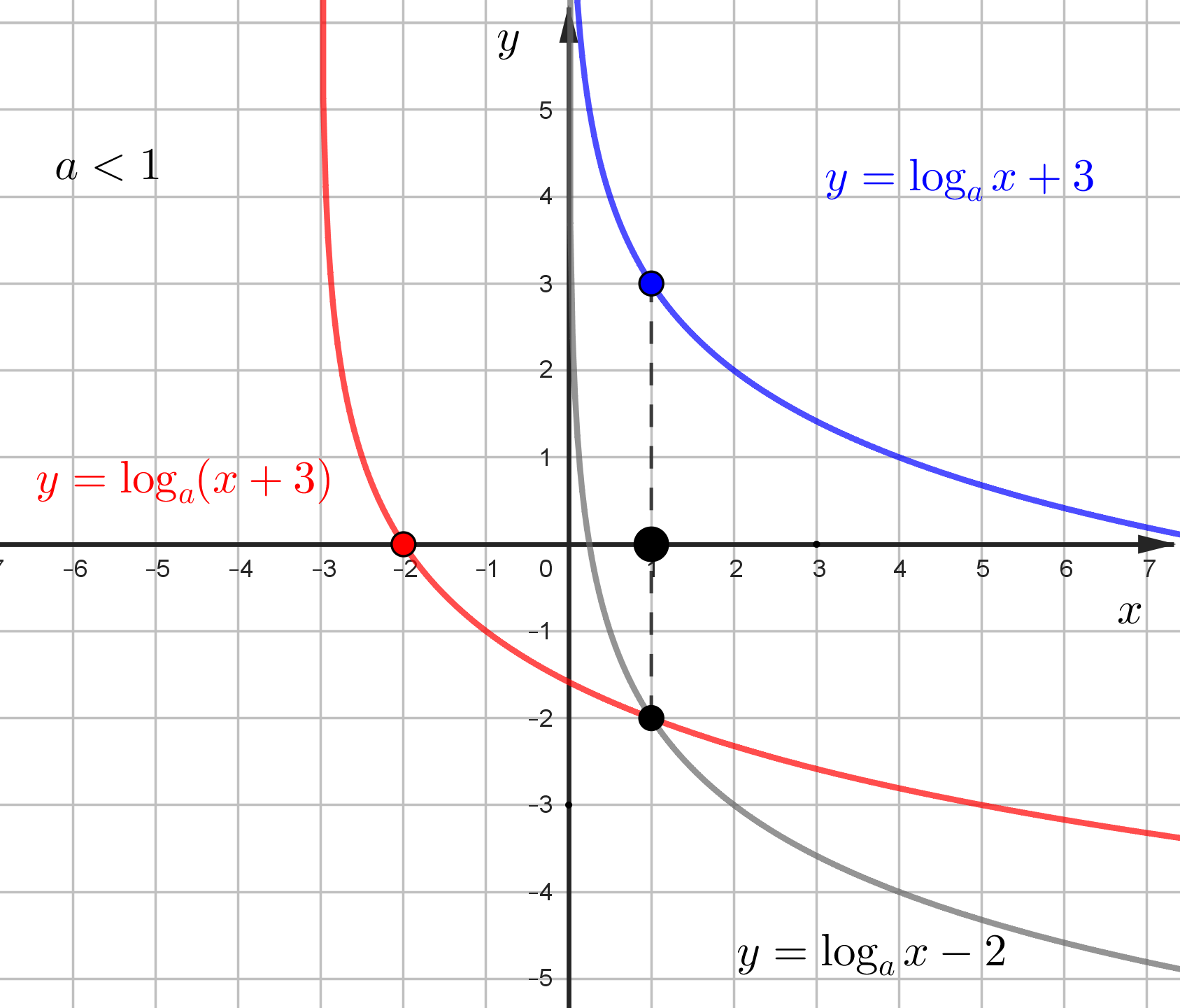
График показательной функции
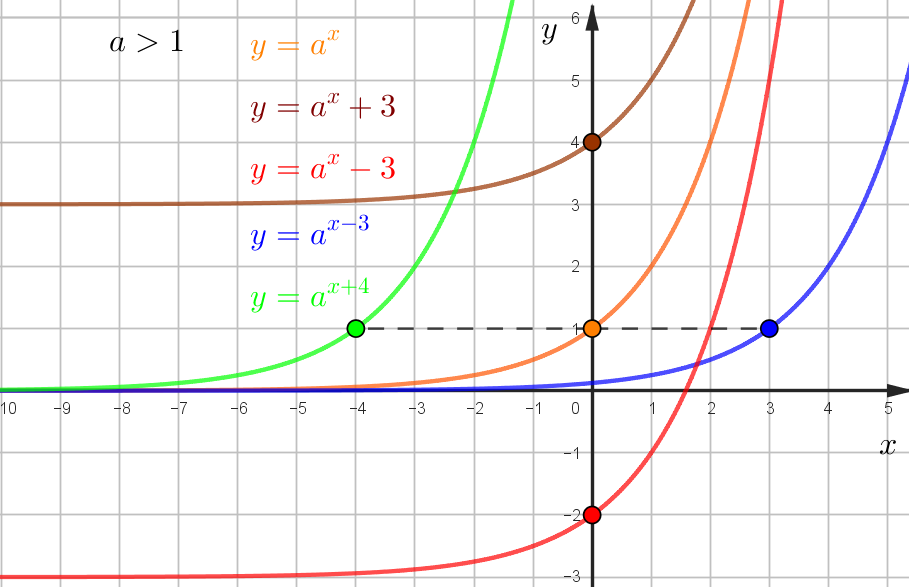
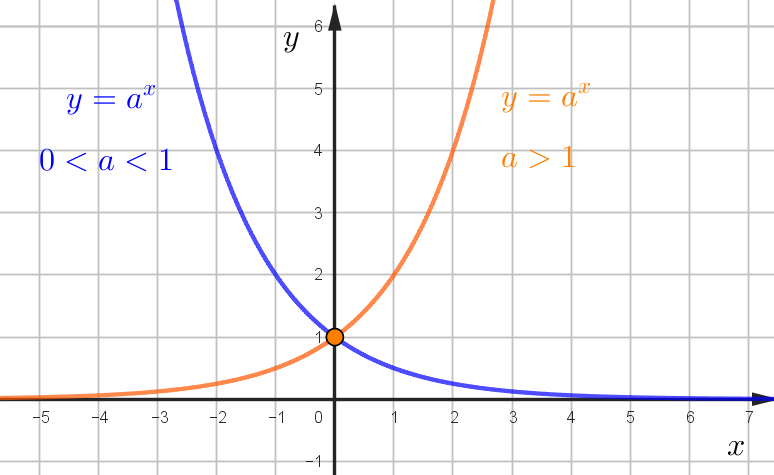
\(y=a^x\) при любом значении \(a\) проходит через точку (0;1).
\(a>1\) - функция возрастает,
\(0<a<1\) - убывает
\(y=a^x+c\), \(c\) - подъем/спуск
Например, \(y=a^x+3\) пересекает ось \(y\) в точке 4 (на 3 единицы выше точки (0;1))
\(y=(a+b)^x\), \(b\) - сдвиг вправо/влево. Смотрим, куда перемещается точка \((0;1)\)
Например, \(y=a^{x+4}\) \(b=4\), поэтому он сдвинулся влево на 4
График корня
\(y=k\sqrt{x+b}\), \(b\) - сдвиг вправо/влево
\(y=k\sqrt{x}+c\), \(c\)-вверх/вниз
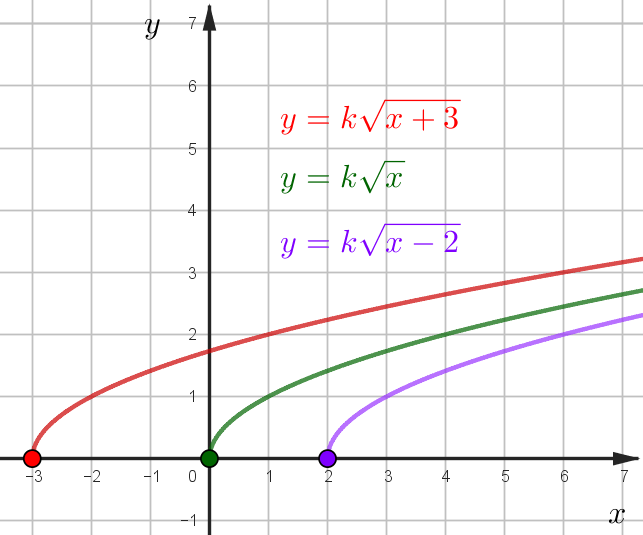
\(k<0\)
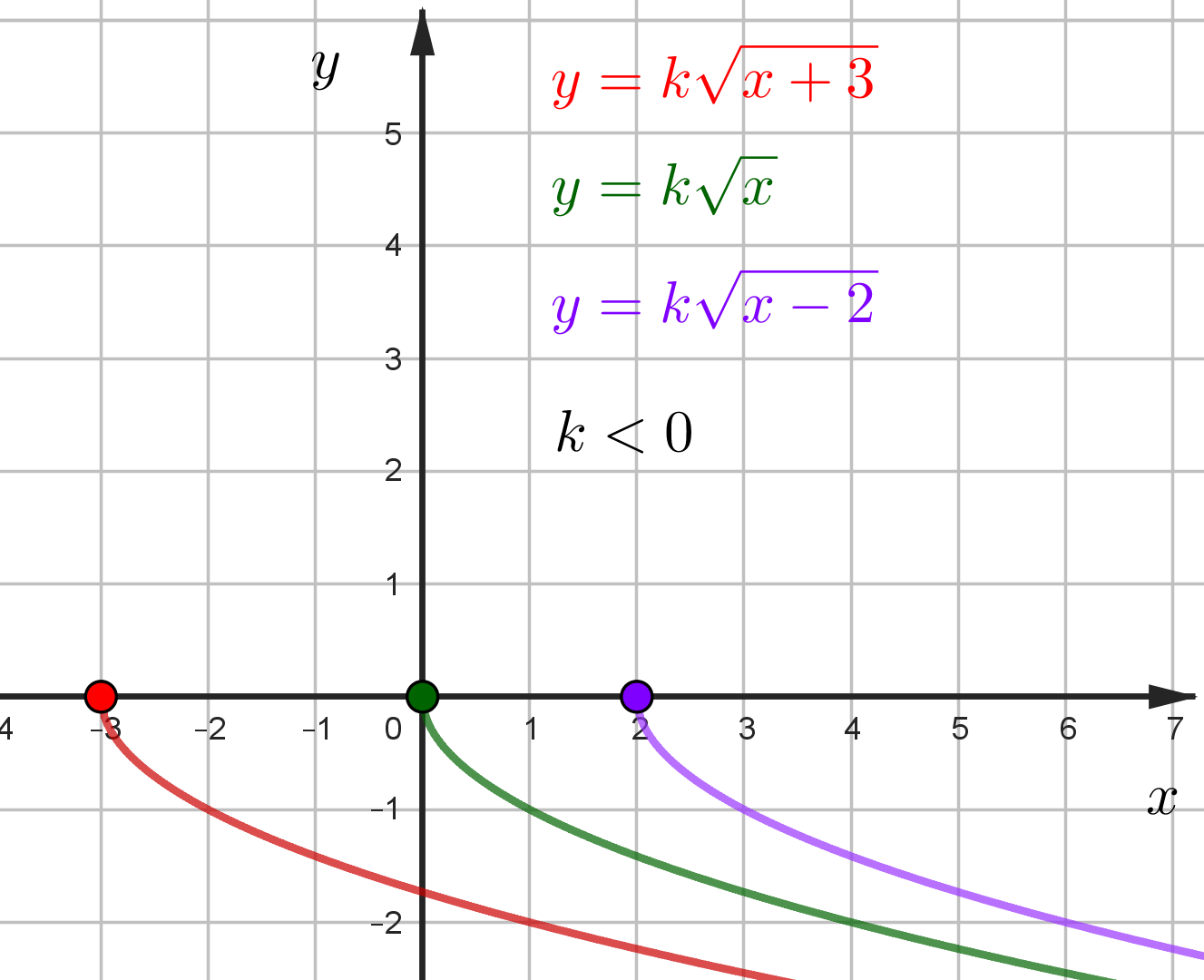
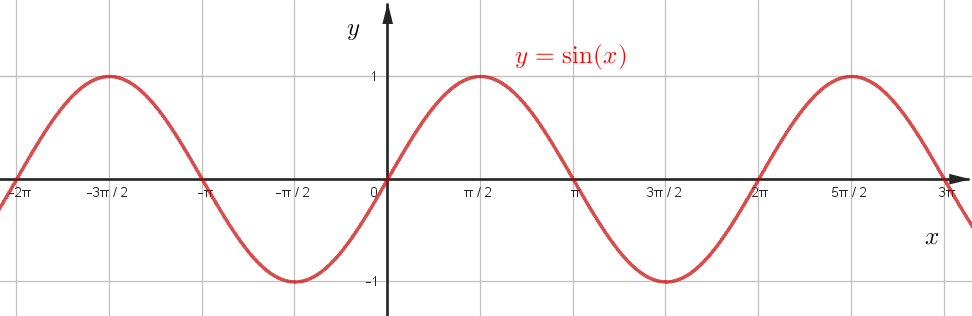
График тригонометрической функции
\(y=\sin x\)
\(y=\cos x\)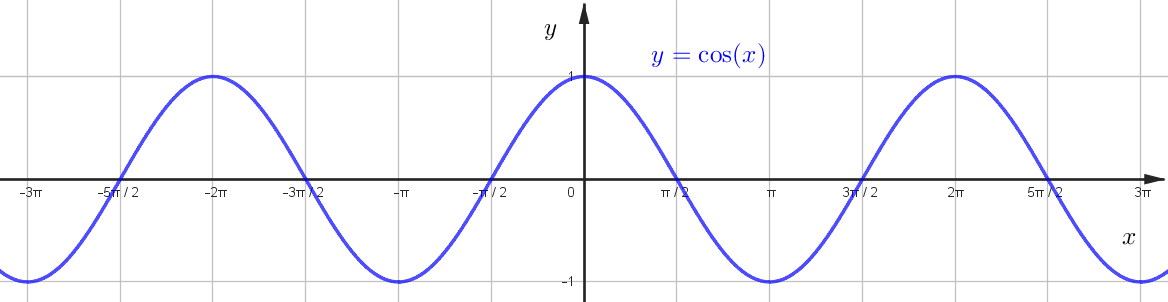
\(y=1,5 \cos x\)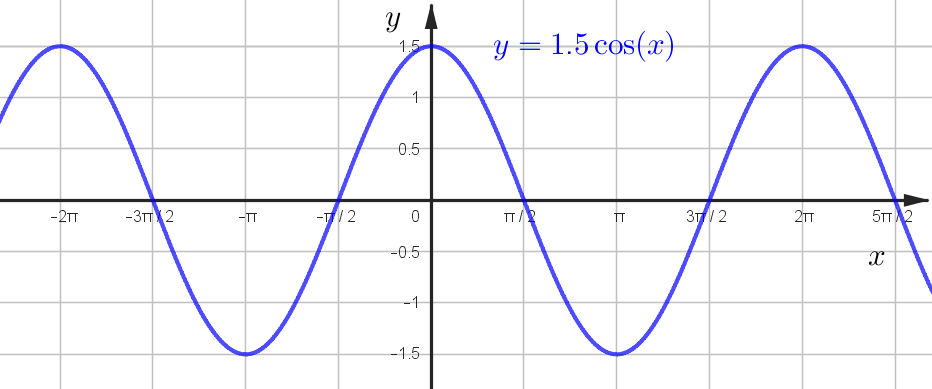
\(y=1.5\sin x-2\)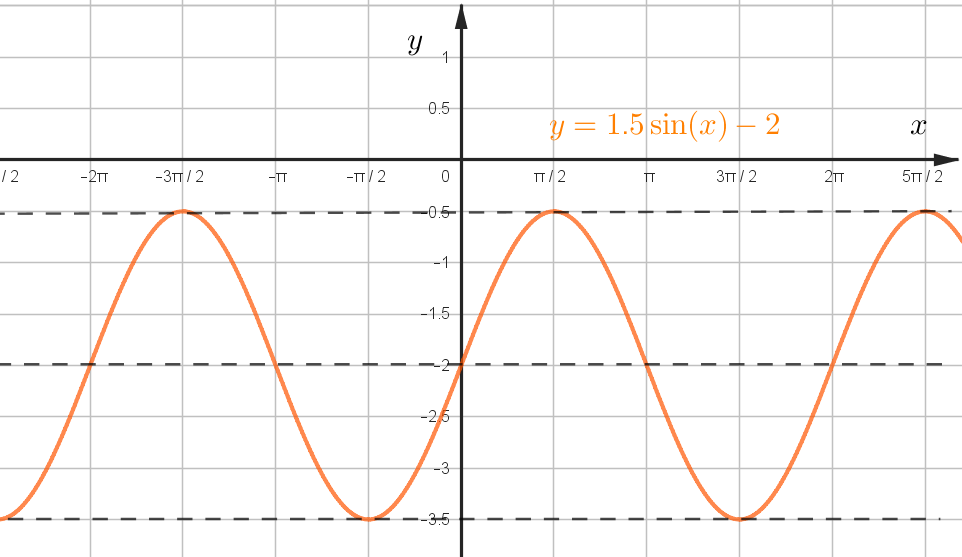
Бесплатные уроки по 11 заданию ЕГЭ в ТЕЛЕГРАММ

11 задание ЕГЭ с видеоразборами
Банк заданий ЕГЭ по профильной математике
Как решать 11 задание ЕГЭ по профильной математике. Видеоурок с разбором всех прототипов