Способы решения систем уравнений
Способы решения систем уравнений
В данной статье мы рассмотрим различные способы решения систем уравнений.
Пример - разобранные примеры. Задача - задачи для самостоятельного решения. Для всех задач в конце статьи есть ответы, а также к некоторым из них - подсказки.
Способ 1. Метод подстановки
В одном из уравнений системы (которое является более простым) выражаем одну переменную через другую, а затем полученное выражение подставляем во второе уравнение системы. Тогда полученная система будет равносильна исходной, а второе уравнение будет зависеть лишь от одной переменной. Дальше решаем второе уравнение, получаем одну из переменных, подставляем найденное значение в первое уравнение и находим пару решений. Ответ записывается в виде \((x; y)\).
Пример 1.
\(\left\{ \begin{gathered}
3x+2y=2\hfill\\
4x+y=6\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
3x+2y=2\hfill\\
y=6-4x\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
3x+2(6-4x)=2\hfill\\
y=6-4x\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x=2\hfill\\
y=6-4x\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x=2\hfill\\
y=-2\hfill
\end{gathered} \right.\)
Ответ: \((2; -2)\)
Здесь мы выразили переменную \(y\) из второго уравнения, потому что так было проще, ведь перед ним не было коэффициента. Дальше подставили это выражение в первое уравнение системы, нашли оттуда \(x\), а затем из второго уравнения \(y\).
Пример 2.
\(\left\{ \begin{gathered}
x+y=3\hfill\\
y+z=8\hfill\\
x+2y+3z=23\hfill
\end{gathered} \right.\)
Выразим из первого уравнения системы \(x=3-y\) и подставим в третье, так как во втором нет переменной \(x\). Получаем равносильную систему.
\(\left\{ \begin{gathered}
x=3-y\hfill\\
y+z=8\hfill\\
3-y+2y+3z=23\hfill
\end{gathered} \right.
\Leftrightarrow
\left\{ \begin{gathered}
x=3-y\hfill\\
y+z=8\hfill\\
y+3z=20\hfill
\end{gathered} \right.\)
Выразим из второго уравнения системы \(y=8-z\) и подставим в третье. Получаем равносильную систему.
\(\left\{ \begin{gathered}
x=3-y\hfill\\
y=8-z\hfill\\
8-z+3z=20\hfill
\end{gathered} \right.
\Leftrightarrow
\left\{ \begin{gathered}
x=3-y\hfill\\
y=8-z\hfill\\
2z=12\hfill
\end{gathered} \right.\)
Из третьего уравнения находим, что \(z=6\). Тогда из второго \(y=2\) и из первого \(x=1\).
Ответ: \((1; 2; 6)\)
Пример 3.
\(\left\{ \begin{gathered}
x^2=7y+2\hfill\\
x^2+2=7y+y^2\hfill
\end{gathered} \right.\)
В первом уравнение системы у нас уже выражен \(x^2\), поэтому, подставив это выражение во второе уравнение, мы получим уравнение, зависящее только от \(y\).
\(\left\{ \begin{gathered}
x^2=7y+2\hfill\\
7y+2+2=7y+y^2\hfill
\end{gathered} \right.\)
Отдельно решим второе уравнение: \(7y+2+2=7y+y^2 \Leftrightarrow\) \(y^2=4 \Leftrightarrow\) \(y=\pm2\).
Теперь каждое значение \(y\) по отдельности подставим в первое уравнение системы и найдём \(x\). При \(y=2\) получаем \(x^2=16\Leftrightarrow x=\pm4\). При \(y=-2\) будет \(x^2=-12 \Rightarrow x\in\varnothing\). Следовательно, у нас две пары решений.
Ответ: \((4; 2), (-4; 2)\)
Задачи для тренировки
Задача 1.
\(\left\{ \begin{gathered}
x+5y=7\hfill\\
3x=4+2y\hfill
\end{gathered} \right.\)
Задача 2.
\(\left\{ \begin{gathered}
2x+3y=5\hfill\\
3x-y=-9\hfill
\end{gathered} \right.\)
Способ 2. Метод сложения
Этот способ заключается в том, что одно из уравнений системы мы можем заменить суммой этого уравнения со вторым, при этом второе уравнение системы нужно оставить без изменений. Делается это в том случае, если в этих уравнения у нас есть переменные с одинаковыми коэффициентами, но разными знаками (например, \(3x\) и \(-3x\)). Тогда, сложив уравнения (левая часть складывается с левой, правая с правой), данная переменная уйдёт, и останется уравнение от одной переменной.
Поэтому первым шагом, если это необходимо, нужно отдельно умножить уравнения на числа так, чтобы при одной из переменных коэффициенты стали противоположенными числами. Далее почленно складываем левые и правые части, решаем уравнение, находим первую переменную, затем вторую и пишем ответ.
Пример 4.
\(\left\{ \begin{gathered}
x+2y=1\hfill\\
3x-y=-18\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+2y=1\hfill\\
6x-2y=-36\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+2y=1\hfill\\
6x-2y+x+2y=-36+1\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+2y=1\hfill\\
7x=-35\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x=-5\hfill\\
y=3\hfill
\end{gathered} \right.\)
Ответ: \((-5; 3)\)
Здесь мы видим в первом уравнение \(2y\), а во втором \(-y\) и хотим от этой переменной избавиться. Для этого всё второе уравнение умножаем на два. Далее первое уравнение оставляем без изменений (можно оставлять любое, но первое просто легче), а второе заменяем на сумму этих двух, складывая левую часть с левой, а правую с правой. Отсюда получаем значение \(x\), подставляем его в первое уравнение и получаем \(y\).
Пример 5.
\(\left\{ \begin{gathered}
x+y^2=2\hfill\\
x^2+2y^2=3\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
-2x-2y^2=-4\hfill\\
x^2+2y^2=3\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+y^2=2\hfill\\
x^2-2x=-1\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+y^2=2\hfill\\
x^2-2x+1=0\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
y^2=1\hfill\\
x=1\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
y=\pm1\hfill\\
x=1\hfill
\end{gathered} \right.\)
Поэтапно разберём этот пример. У нас есть система квадратных уравнений. Мы видим, что в обоих уравнениях присутствует \(y^2\). И, чтобы при сложение они ушли, нужно первое уравнение умножить на \(-2\), после чего складываем уравнения. Как мы уже говорили, вторым уравнение можно записать любое из тех, что было (то есть или \(-2x-2y^2=-4\), или \(x^2+2y^2=3\)). Но первое ведь равно исходному \(x+y^2=2\), которое является более простым, так что пишем его. Дальше мы решаем уравнение, зависящее только от \(x\) и получаем единственный корень. Если бы мы получили два значения \(x\), то каждый по отдельности нужно было бы подставить в первое уравнение и найти соответствующий ему \(y\). Здесь же обоим \(y\)-ам соответствует единственный \(x\). Пишем ответ: \((1; 1); (1; -1)\).
Задачи для тренировки
Задача 3.
\(\left\{ \begin{gathered}
x-3y=11\hfill\\
2x+4y+8=0\hfill
\end{gathered} \right.\)
Задача 4.
\(\left\{ \begin{gathered}
5(x+2y)=x+8\hfill\\
4(x-3y)=50-y\hfill
\end{gathered} \right.\)
Задача 5.
\(\left\{ \begin{gathered}
y+xy=12\hfill\\
x+xy=15\hfill
\end{gathered} \right.\)
Способ 3. Разложение на множители
Если одно из уравнений системы имеет вид \(f_1(x; y)\cdot f_2(x; y)=0\), решением которого является совокупность из двух уравнений \(f_1(x; y)=0\) и \(f_2(x; y)=0\), то такую систему можно разложить на совокупность двух систем. В первой системе должно быть уравнение \(f_1(x; y)=0\), второе уравнение исходной системы, а также должна быть определена \(f_2(x; y)\). Во второй системе должно быть уравнение \(f_2(x; y)=0\), второе уравнение исходной системы, а также должна быть определена \(f_1(x; y)\). Разберём на конкретном примере.
Пример 6.
\(\left\{ \begin{gathered}
x+2y=8\hfill\\
x^2+5x=0\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{ \begin{gathered}
x+2y=8\hfill\\
x(x+5)=0\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left[ \begin{gathered}
\left\{ \begin{gathered}
x+2y=8\hfill\\
x=0\hfill
\end{gathered}\right. \hfill\\
\left\{ \begin{gathered}
x+2y=8\hfill\\
x=-5\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow\) \(\left[ \begin{gathered}
\left\{ \begin{gathered}
y=4\hfill\\
x=0\hfill
\end{gathered}\right. \hfill\\
\left\{ \begin{gathered}
y=6,5\hfill\\
x=-5\hfill
\end{gathered}\right.
\end{gathered}\right.\)
В данном случае можно было решать иначе: вначале отдельно найти оба значения \(x\) из второго уравнения, а потом по очереди подставлять их в первое уравнение. В целом, мы это и сделали, только оформили в совокупность двух систем.
Ответ: \((0 ; 4); (-5 ; 6,5)\)
Задачи для тренировки
Задача 6.
\(\left\{ \begin{gathered}
(x-5)(y-8)=0\hfill\\
\dfrac{y-6}{x+y-11}=4\hfill
\end{gathered} \right.\)
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Способ 4. Метод замены переменной
Пример 7.
\(\left\{ \begin{gathered}
3 x=y+1\hfill\\
7^{y-2 x+2}=7 \cdot 7^{y-4 x}+6\hfill
\end{gathered} \right.\)
Сначала выразим из первого уравнения \(y=3x-1\) и подставим это во второе: \(7^{3x-1-2x+2}=7\cdot7^{3x-1-4x}+6\Leftrightarrow\) \( 7^{x+1}=7\cdot7^{-x-1}+6\).
А теперь сделаем замену \(7^{x+1}=t\), тогда \(7^{-x-1}=7^{-(x+1)}=\left(7^{x+1}\right)^{-1}=t^{-1}=\dfrac{1}{t}\).
Теперь второе уравнение системы имеет такой вид: \(t=\dfrac{7}{t}+6\). Умножим обе части уравнения на \(t\neq0\), ведь за \(t\) мы взяли показательную функцию. Тогда решим квадратное уравнение \(t^2-6t-7=0\) получим, что \(t=-1\) или \(t=7\). Первый корень отбрасываем ввиду того, что \(t>0\). А со вторым производим обратную замену: \(7^{x+1}=7\Leftrightarrow x+1=1\Leftrightarrow x=0\). Тогда из первого уравнения: \(y=-1\).
Ответ: \((0; -1)\)
Пример 8.
\(\left\{ \begin{gathered}
x+y=-8\hfill\\
x^2+y^2+6 x+2 y=0\hfill
\end{gathered} \right.\)
Преобразуем второе уравнение системы, чтобы выделить в нём полные квадраты:
\(x^2+y^2+6 x+2 y=0 \Leftrightarrow\) \(x^2+6 x+9+y^2+2 y+1=9+1 \Leftrightarrow\) \((x+3)^2+(y+1)^2=10\).
Сделаем замену \(x+3=a, y+1=b\). Тогда \(x=a-3\) и \(y=b-1\). Следовательно, \(x+y=a-3+b-1=a+b-4\).
Тогда исходная система принимает такой вид:
\(\left\{ \begin{gathered}
a+b=-4\hfill\\
a^2+b^2=10\hfill
\end{gathered} \right.\)
Выражаем из первого уравнения \(a=-b-4\) и подставляем во второе. Проделав преобразования, получаем, что \(a=-1\) или \(a=-3\).
\(\left[ \begin{gathered}
\left\{ \begin{gathered}
a=-1\hfill\\
b=-3\hfill
\end{gathered}\right. \hfill\\
\left\{ \begin{gathered}
a=-3\hfill\\
b=-1\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow
\left[ \begin{gathered}
\left\{ \begin{gathered}
x=-1-3=-4\hfill\\
y=-3-1=-4\hfill
\end{gathered}\right. \hfill\\
\left\{ \begin{gathered}
x=-3-3=-6\hfill\\
y=-1-1=-2\hfill
\end{gathered}\right.
\end{gathered}\right.\)
Ответ: \((-4 ;-4); (-6 ;-2)\)
Пример 9.
\(\left\{ \begin{gathered}
x^2+2 x y+y^2-4 x-4 y-45=0\hfill\\
x^2-2 x y+y^2-2 x+2 y-3=0\hfill
\end{gathered} \right.\)
В обоих уравнениях свернём все полные квадраты. Тогда система примет вид:
\(\left\{ \begin{gathered}
(x+y)^2-4(x+y)-45=0\hfill\\
(x-y)^2-2(x-y)-3=0\hfill
\end{gathered} \right.\)
Далее сделаем замену, которую сразу видно: \(x+y=a\) и \(x-y=b\).
\(\left\{ \begin{gathered}
a^2-4 a-45=0\hfill\\
b^2-2 b-3=0\hfill
\end{gathered} \right.\)
По отдельности решаем каждое уравнение и получаем такую систему:
\(\left\{ \begin{gathered}
a^2-4 a-45=0\hfill\\
b^2-2 b-3=0\hfill
\end{gathered} \right.
\Leftrightarrow\) \(\left\{\begin{gathered}
\left[\begin{gathered}
a=9\hfill\\
a=-5\hfill\\
\end{gathered}\right.\\
\left[\begin{gathered}
b=1\hfill\\
b=-3\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
\left[\begin{gathered}
x+y=9\hfill\\
x+y=-5\hfill\\
\end{gathered}\right.\\
\left[\begin{gathered}
x-y=1\hfill\\
x-y=-3\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{ \begin{gathered}
x+y=9\hfill\\
x-y=1\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x+y=9\hfill\\
x-y=-3\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x+y=-5\hfill\\
x-y=1\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x+y=-5\hfill\\
x-y=-3\hfill
\end{gathered} \right.
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{ \begin{gathered}
x=5\hfill\\
y=4\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x=3\hfill\\
y=6\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x=-2\hfill\\
y=-3\hfill
\end{gathered} \right.\\
\left\{ \begin{gathered}
x=-4\hfill\\
y=-1\hfill
\end{gathered} \right.
\end{gathered}\right.\)
Итого имеем 4 пары решений: \((5;4), (3;6), (-2;-3), (-4;-1).\)
Здесь важно понимать переход от системы двух (или более) совокупностей. Пусть у нас есть общая система, в которой находится, к примеру, две совокупности.
\(\left\{\begin{gathered}
\left[\begin{gathered}
f_1(x;y)=0\hfill\\
f_2(x;y)=0\hfill\\
\end{gathered}\right.\hfill\\
\left[\begin{gathered}
f_3(x;y)=0\hfill\\
f_4(x;y)=0\hfill
\end{gathered}\right.\hfill\\
\end{gathered}\right.\)
Это означает, что для выполнения первого условия системы нам подходит ИЛИ \(f_1(x;y)=0\), ИЛИ \(f_2(x;y)=0\); для выполнения второго условия системы подходит ИЛИ \(f_3(x;y)=0\), ИЛИ \(f_4(x;y)=0\). Предположим, что первое условие системы выполняется при \(f_1(x;y)=0\). Тогда для него есть два варианта: \(f_3(x;y)=0\) или \(f_4(x;y)=0\). Отсюда получаем две новые системы решений. И аналогично: если первое условие изначальной системы выполняется при \(f_2(x;y)=0\), то к нему также может быть два варианта: \(f_3(x;y)=0\) или \(f_4(x;y)=0\). Итого у нас ровно 4 системы решений, которые мы объединяем в общую совокупность и получаем следующее:
\(\left[\begin{gathered}
\left\{ \begin{gathered}
f_1(x;y)=0\hfill\\
f_3(x;y)=0\hfill
\end{gathered} \right.\hfill\\
\left\{ \begin{gathered}
f_1(x;y)=0\hfill\\
f_4(x;y)=0\hfill
\end{gathered} \right.\hfill\\
\left\{ \begin{gathered}
f_2(x;y)=0\hfill\\
f_3(x;y)=0\hfill
\end{gathered} \right.\hfill\\
\left\{ \begin{gathered}
f_2(x;y)=0\hfill\\
f_4(x;y)=0\hfill
\end{gathered} \right.\hfill\\
\end{gathered}\right.\)
Задачи для тренировки
Задача 7.
\(\left\{ \begin{gathered}
\dfrac{1}{x-y}+x^2=1\hfill\\
\dfrac{x^2}{x-y}=-2\hfill
\end{gathered} \right.\)
Задача 8.
\(\left\{ \begin{gathered}
\dfrac{3}{2 x-y}+\dfrac{1}{2 x+y}=\dfrac{2}{5}\hfill\\
\dfrac{7}{2 x-y}+\dfrac{2}{2 x+y}=\dfrac{3}{5}\hfill
\end{gathered} \right.\)
Способ 5. Метод умножение/деления
Если есть система, состоящая из уравнений \(A=B\) и \(C=D\), то можно, аналогично методу сложения уравнений, перейти к системе, одно из уравнений которой принимает вид \(AC=BD\) или \(\dfrac{A}{C}=\dfrac{B}{D}\). Второе уравнение новой системы - одно из исходных уравнений. И также стоит понимать, что в случае деления необходимо проконтролировать, что \(C\neq0\) и \(D\neq0\), чтобы в знаменателе не получились нули.
Пример 10.
\(\left\{\begin{gathered}
x^5y^7=32\hfill\\
x^7y^5=128\hfill
\end{gathered}\right.\)
Здесь мы сразу понимаем, что \(x\neq0\) и \(y\neq0\). Тогда делим первое уравнение системы на второе: \(\dfrac{x^5y^7}{x^7y^5}=\dfrac{32}{128}\Leftrightarrow\dfrac{y^2}{x^2}=\dfrac{1}{4}\Leftrightarrow\dfrac{y}{x}=\pm\dfrac{1}{2}\). Тогда \(x=2y\) или \(x=-2y\)
Подставим поочерёдно получившиеся равенства в одной из двух уравнений исходной системы, например, в первое. При подстановке \(x=2y\) поучаем следующее: \((2y)^5y^7=32\Leftrightarrow32y^5y^7=32=\Leftrightarrow\) \(y^{12}=1\Leftrightarrow\) \(y=\pm1\). И далее находим соответствующие значения для \(x\): при \(y=1\) будет \(x=2\); при \(y=-1\) будет \(x=-2\). При подстановке \(x=-2y\) получаем \(y^{12}=-1\), а такое уравнение не имеет корней.
Ответ: \((2;1), (-2;-1)\)
Пример 11.
\(\left\{\begin{gathered}
5 \sqrt[3]{x^5 y^2}=4\left(x^2+y^2\right)\hfill\\
3 \sqrt[3]{x y^4}=x^2-y^2\hfill
\end{gathered}\right.\)
Сразу заметим, что если \(x=0\), то и \(y=0\), то есть пара \((0;0)\) - решение системы. Запишем её в ответ и дальше будем работать при \(x\neq0\) и \(y=\neq0\).
Умножим первое уравнение системы на второе: \(5 \sqrt[3]{x^5 y^2} \cdot 3 \sqrt[3]{x y^4}=4\left(x^2+y^2\right)(x^2-y^2) \Leftrightarrow\) \(15\sqrt[3]{x^6y^6}=4(x^4-y^4)\Leftrightarrow\) \(15x^2y^2=4x^4-4y^4\Leftrightarrow\) \(4x^4-15x^2y^2-4y^4=0\).
Последнее уравнение решим как квадратное относительно \(x^2\) (можно сделать замену \(x^2=t\)). Получаем, что \(x^2=\dfrac{15y^2\pm\sqrt{225y^4+64y^4}}{8}=\) \(\dfrac{15y^2\pm17y^2}{8}=\) \(\left[\begin{gathered}4y^2\hfill\\-\dfrac{1}{4}y^2\hfill\end{gathered}\right.\)
Очевидно, что второе уравнение \(x^2=-\dfrac{1}{4}y^2\) не имеет корней. Первое же уравнение \(x^2=4y^2\) равносильно \(x=\pm2y\).
Если мы подставим \(x=2y\) в \(3 \sqrt[3]{x y^4}=x^2-y^2\), то получим \(3\sqrt[3]{2y^5}=3y^2\Leftrightarrow\) \(\sqrt[3]{2y^5}=y^2\Leftrightarrow\) \(2y^5=y^6 \Leftrightarrow\) \(y=2\) (так как случай \(y=0\) мы уже разобрали). Тогда пара решений: (4;2).
Если мы подставим \(x=-2y\) в \(3 \sqrt[3]{x y^4}=x^2-y^2\), то получим \(3\sqrt[3]{-2y^5}=3y^2\Leftrightarrow\) \(\sqrt[3]{-2y^5}=y^2\Leftrightarrow\) \(-2y^5=y^6 \Leftrightarrow\) \(y=-2\) (так как случай \(y=0\) мы уже разобрали). Тогда пара решений: (4;-2).
Ответ: \((0,0) ;(4,2) ;(4,-2)\)
Задачи для тренировки
Задача 9.
\(\left\{\begin{gathered}
x^2y^3=16\hfill\\
x^3y^2=2\hfill
\end{gathered}\right.\)
Задача 10.
\(\left\{\begin{gathered}
x+xy^3=9\hfill\\
xy+xy^2=6\hfill
\end{gathered}\right.\)
Задача 11.
\(\left\{\begin{gathered}
\sqrt{\dfrac{20y}{x}}=\sqrt{x+y}+\sqrt{x-y}\hfill\\
\sqrt{\dfrac{16x}{5y}}=\sqrt{x+y}-\sqrt{x-y}\hfill
\end{gathered}\right.\)
Способ 6. Однородные системы уравнений
Многочлен \(P(x;y)\) называется однородным, если все слагаемые, содержащие переменную, имеют одинаковую степень. К примеру, многочлен второй степени выглядит так: \(ax^2+bxy+cy^2=0\). То есть все слагаемые с переменными (\(x^2, xy, y^2\)) имеют одинаковую степень, равную двум.
Уравнение называется однородным, если однородный многочлен равняется нулю: \(P(x;y)=0\).
Система называется однородной, если одна содержит однородные многочлены равной степени, каждый из которых равняется произвольному числу \(d_i\).
\(\left\{\begin{gathered}
a_1x^2+b_1xy+c_1y^2=d_1\hfill\\
a_2x^2+b_2xy+c_2y^2=d_2\hfill
\end{gathered}\right.\)
Пример 12.
\(\left\{\begin{gathered}
2x^2-3xy+y^2=6\hfill\\
3x^2-2xy-2y^2=3\hfill
\end{gathered}\right.\)
Чтобы решить однородную систему уравнений, нужно методом сложения привести её в однородному уравнению так, чтобы у него не было свободных членов (то есть коэффициент \(d=0\)). Для этого второе уравнение системы умножим на \(-2\), а затем сложим уравнения.
\(\left\{\begin{gathered}
2x^2-3xy+y^2=6\hfill\\
-6x^2+4xy+4y^2=-6\hfill
\end{gathered}\right.\)
После сложения получаем однородное уравнение: \(-4x^2+xy+5y^2=0\). Его можно решать как квадратное уравнение относительно переменной \(x\), или же путём деления всего уравнения на \(y\neq0\) и замены \(\dfrac{x}{y}=t\). Решим первым способом. Тогда \(x=\dfrac{-y\pm\sqrt{y^2-4\cdot(-4)\cdot5y^2}}{-8}=\) \(\dfrac{-y\pm9y}{-8}=\) \(\left[\begin{gathered}-y\hfill\\ \dfrac{5y}{4}\end{gathered}\right.\)
Теперь остаётся подставить поочерёдно \(x=-y\) и \(x=\dfrac{5y}{4}\) в любое из изначальных уравнений и получить 4 пары решений. Выполните это самостоятельно
Ответ: \((-1 ; 1) ;(1 ;-1) ;(5 ; 4) ;(-5 ;-4)\)
Пример 13.
\(\left\{\begin{gathered}
(x-y)^2+4(x+y)^2=5\hfill\\
\dfrac{1}{x^2-2 x y+9 y^2}=\dfrac{1}{9}\hfill
\end{gathered}\right.\)
Вначале упростим данную систему: в первом уравнение раскроем полные квадраты и приведём подобные слагаемые, а во втором воспользуемся свойством пропорции.
\(\left\{\begin{gathered}
5 x^2+6 x y+5 y^2=5\hfill\\
x^2-2 x y+9 y^2=9\hfill
\end{gathered}\right.\)
Теперь это однородная система. Чтобы её решить, умножим первое уравнение на 9, второе на -5, а затем сложим получившиеся уравнения.
\(\left\{\begin{gathered}
45 x^2+54 x y+45 y^2=45\hfill\\
-5x^2+10 x y-45 y^2=-45\hfill
\end{gathered}\right.\)
В результате сложения получили однородное уравнение: \(40x^2+64xy=0 \Leftrightarrow x(5x+8y)=0\). Тогда \(x=0\) или \(5x+8y=0 \Leftrightarrow x=-\dfrac{8}{5}y\).
Подставим \(x=0\) в первое уравнение: \(y^2+4y^2=5 \Leftrightarrow 5y^2=5 \Leftrightarrow y=\pm1\).
Подставим \(x=-\dfrac{8}{5}y\) в первое уравнение: \(5\left(-\dfrac{8}{5}y\right)^2+6y\left(-\dfrac{8}{5}y\right)+5y^2=5 \Leftrightarrow\) \(\dfrac{64}{5}y^2-\dfrac{48}{5}y+5y^2=5 \Leftrightarrow\) \(\dfrac{41}{5}y^2=5 \Leftrightarrow\) \(y=\pm\dfrac{5}{\sqrt{41}}\). Тогда получаются ещё две пары решений: \(\left(\dfrac{8}{\sqrt{41}}; -\dfrac{5}{\sqrt{41}}\right),\) \(\left(-\dfrac{8}{\sqrt{41}};\dfrac{5}{\sqrt{41}}\right) \).
Ответ: \((0;1), (0;-1),\) \(\left(\dfrac{8}{\sqrt{41}};-\dfrac{5}{\sqrt{41}}\right),\) \(\left(-\dfrac{8}{\sqrt{41}};\dfrac{5}{\sqrt{41}}\right)\)
Задачи для тренировки
Задача 12.
\(\left\{\begin{gathered}
x^2-3 y^2+3 x y=1\hfill\\
2 x^2-x y+y^2=2\hfill
\end{gathered}\right.\)
Задача 13.
\(\left\{\begin{gathered}
3 x^2+5 x y-2 y^2=20\hfill\\
x^2+x y+y^2=7\hfill
\end{gathered}\right.\)
Задача 14.
\(\left\{\begin{gathered}
2 y^2-x^2+x y=0\hfill\\
x^2-x y-y^2+3 x+7 y+3=0\hfill
\end{gathered}\right.\)
Способ 7. Симметрические системы уравнений
Уравнение называется симметрическим, если при смене \(x\) и \(y\) местами (подстановки вместо \(x\) --- \(y\), а вместо \(y\) --- \(x\)) ничего не изменяется. Например, уравнение \(x^2+y^2=2(xy+2)\) является симметрическим, ведь при смене получим \(y^2+x^2=2(yx+2)\), то есть ничего не меняется.
Система называется симметрической, если состоит из симметрических уравнений. Они решаются путём введения замены \(a=x+y\) и \(b=xy\).
Также полезно помнить следующие выражения:
\(x^2+y^2=\) \(x^2+2 x y+y^2-2 x y=\) \((x+y)^2-2 x y=\) \(a^2-2b\)
\(x^3+y^3=\) \((x+y)\left(x^2-x y+y^2\right)=\) \(a \cdot\left(a^2-3 b\right)=\) \(a^3-3 ab\)
\(x^4+y^4=\) \(\left(x^2+y^2\right)^2-2 x^2 y^2=\) \(\left(a^2-2 b\right)^2-2 b^2=\) \(a^4-4 a^2 b+2 b^2\)
Пример 14.
\(\left\{\begin{gathered}
x^2+y^2=20\hfill\\
xy=8\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
a^2-2b=20\hfill\\
b=8\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
a^2=36\hfill\\
b=8\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
a=\pm6\hfill\\
b=8\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
x+y=\pm6\hfill\\
xy=8\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{\begin{gathered}
x+y=6\hfill\\
xy=8\hfill
\end{gathered}\right.\hfill\\
\left\{\begin{gathered}
x+y=-6\hfill\\
xy=8\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{\begin{gathered}
x=4\hfill\\
y=2\hfill
\end{gathered}\right.\hfill\\
\left\{\begin{gathered}
x=2\hfill\\
y=4\hfill
\end{gathered}\right.\hfill\\
\left\{\begin{gathered}
x=-4\hfill\\
y=-2\hfill
\end{gathered}\right.\hfill\\
\left\{\begin{gathered}
x=-2\hfill\\
y=-4\hfill
\end{gathered}\right. \hfill\\
\end{gathered}\right.\)
Ответ: \((4 ; 2) ;(2 ; 4) ;(-4 ;-2) ;(-2 ;-4)\)
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Пример 15.
\(\left\{\begin{gathered}
x^2 y+x y^2=2-2 x-2 y\hfill\\
x+y+5=-x y\hfill
\end{gathered}\right.\)
Преобразуем систему:
\(\left\{\begin{gathered}
xy(x+y)=2-2(x+y)\hfill\\
x+y+5=-x y\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
ab=2-2a\hfill\\
a+5=-b\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
ab=2-2a\hfill\\
b=-a-5\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
a(-a-5)=2-2a\hfill\\
b=-a-5\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left\{\begin{gathered}
a^2+3a+2=0\hfill\\
b=-a-5\hfill
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{\begin{gathered}
a=-1\hfill\\
b=-4\hfill
\end{gathered}\right.\\
\left\{\begin{gathered}
a=-2\hfill\\
b=-3\hfill
\end{gathered}\right.
\end{gathered}\right.
\Leftrightarrow\) \(\left[\begin{gathered}
\left\{\begin{gathered}
x+y=-1\hfill\\
xy=-4\hfill
\end{gathered}\right.\\
\left\{\begin{gathered}
x+y=-2\hfill\\
xy=-3\hfill
\end{gathered}\right.
\end{gathered}\right.\)
Дальнейшее решение систем остаётся в качестве упражнения.
Ответ: \(\left(\dfrac{-1+\sqrt{17}}{2}; \dfrac{-1-\sqrt{17}}{2}\right),\) \(\left(\dfrac{-1-\sqrt{17}}{2}; \dfrac{-1+\sqrt{17}}{2}\right),\) \((1;-3),\) \((-3;1)\)
Задачи для тренировки
Задача 15.
\(\left\{\begin{gathered}
x^2+y^2+x y=7\hfill\\
x+y+x y=5\hfill
\end{gathered}\right.\)
Задача 16.
\(\left\{\begin{gathered}
x^3+y^3=19\hfill\\
(x y+8)(x+y)=2\hfill
\end{gathered}\right.\)
Задача 17.
\(\left\{\begin{gathered}
x^4+x^2 y^2+y^4=91\hfill\\
x^2+x y+y^2=13\hfill
\end{gathered}\right.\)
Способ 8. Графический метод
Если мы хотим решить систему уравнений графическим методом, то нам нужно построить графики, задаваемые каждым из уравнений системы, а затем по графику определить координаты точек пересечения. Однако для того, чтобы удостовериться в правильности найденных точек, их нужно обязательно подставить в исходную систему, ведь очень важную роль здесь играть то, как чётко построен график.
Не всегда построенный график даёт все решения системы, но он может помочь упростить её решение. Например, по графику мы можем узнать точно количество корней, и так же понять, например, что все корни - положительные.
Пример 16.
\(\left\{\begin{gathered}
y=-\dfrac{3}{x}\hfill\\
x+y=-2\hfill
\end{gathered}\right.\)
Первое уравнение системы - гипербола. Второе уравнение - прямая \(y=-x-2\). Построим обе функции.
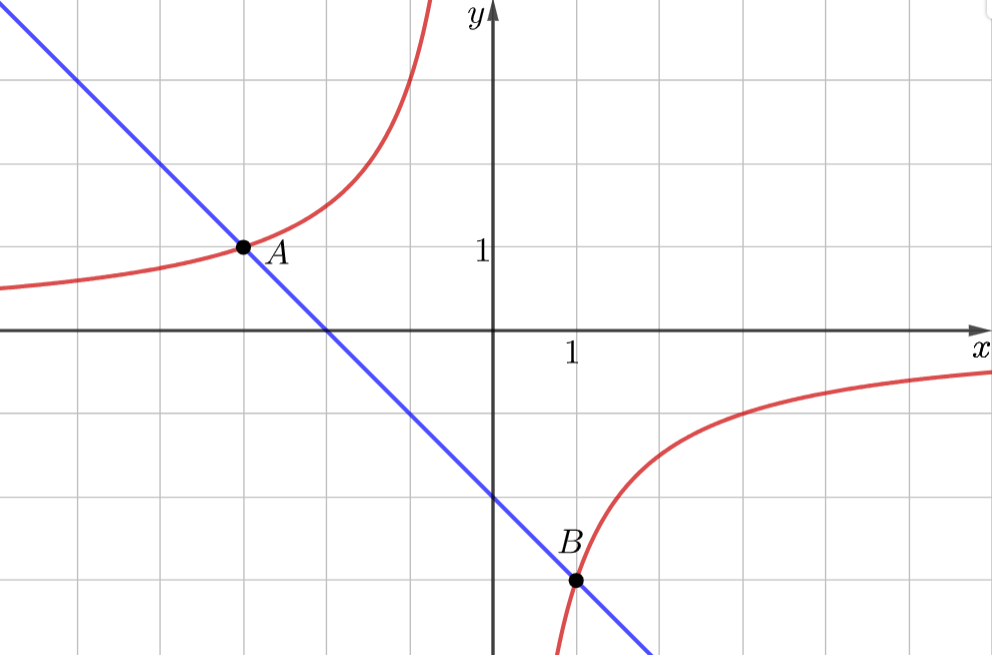
Теперь по графику видно, что решениями исходной системы являются точки \(A (-3;1)\) и \(B (1; -3)\). Подставим каждую из точек по очереди в систему и убедимся в правильности.
A: \(y=-\dfrac{3}{x}\Rightarrow 1=-\dfrac{3}{-3}=1\) и \(x+y=-2 \Rightarrow 1-3=-2\).
B: \(y=-\dfrac{3}{x}\Rightarrow -3=-\dfrac{3}{1}=-3\) и \(x+y=-2 \Rightarrow 1-3=-2\).
Ответ: \((-3; 1), (1; -3)\)
Пример 17.
\(\left\{\begin{gathered}
x^2+y=3\hfill\\
x-y+1=0\hfill
\end{gathered}\right.\)
В первом уравнение системы выделим параболу \(y=-x^2-3\), а во втором прямую \(y=x+1\), изобразим их графически.
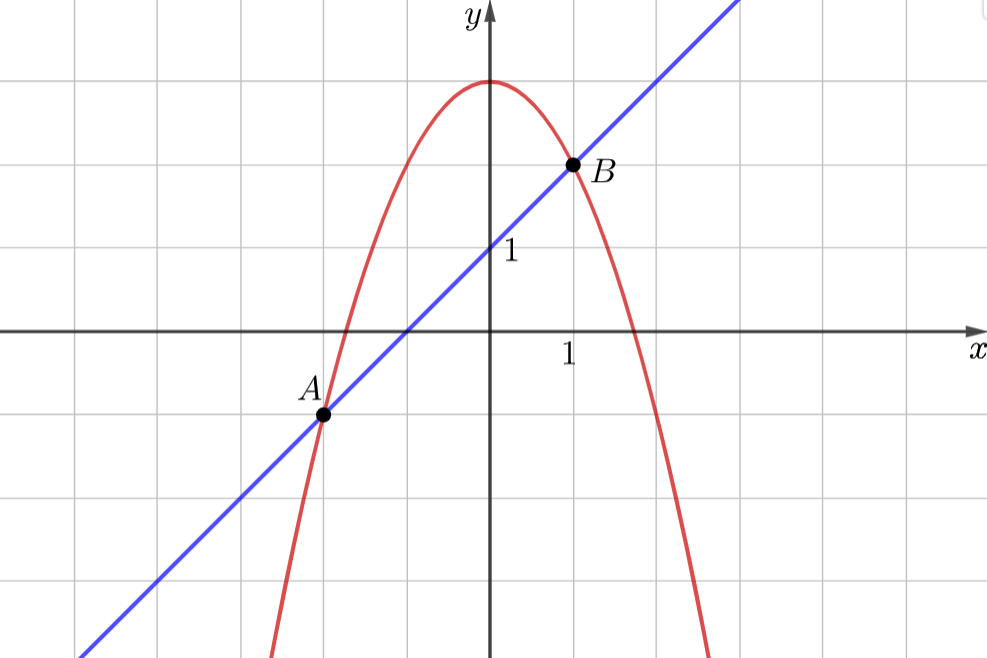
Видим, что они пересекаются в точках \((-2; -1)\) и \((1; 2)\). После проверки данных точек пишем ответ.
Ответ: \((-2; -1), (1; 2)\)
Пример 18.
\(\left\{\begin{gathered}
x+y=-8\hfill\\
x^2+y^2+6 x+8 y=0\hfill
\end{gathered}\right.\)
В первом уравнение системы выделяем прямую \(y=-x-8\). Во втором нужно собрать полные квадраты, чтобы получить уравнение окружности: \(x^2+y^2+6x+8y=0 \Leftrightarrow\) \(x^2+6x+9-9+y^2+8y+16-16=0 \Leftrightarrow\) \((x+3)^2+(y+4)^2=5^2\). Это окружность с центром в точке \((-3; -4)\) и радиусом \(R=5\). Построим графики.
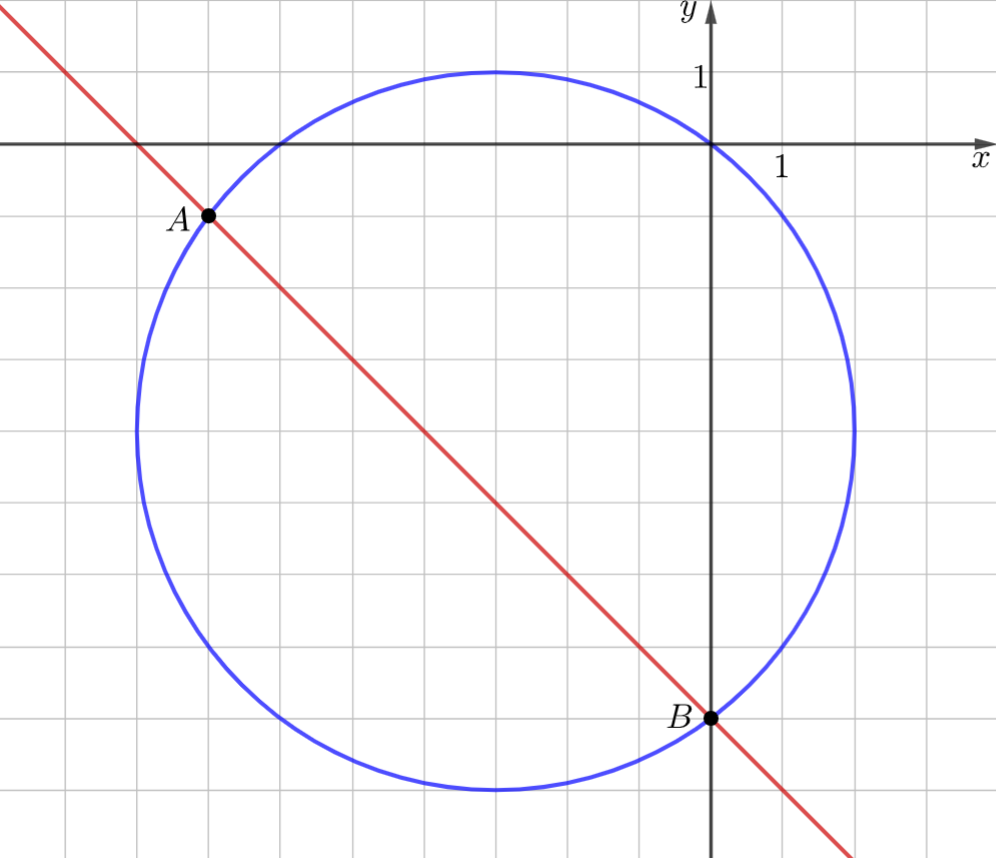
Точки пересечения явно видны. Проверим их, и, так как всё сходится, запишем ответ.
Ответ: \((-7 ;-1) ;(0 ;-8)\)
Пример 19.
\(\left\{\begin{gathered}
x^2-3 x y+2 y^2=0\hfill\\
|y| x+y|x|=2\hfill
\end{gathered}\right.\)
Сначала решим первое уравнение как квадратное относительно переменной \(x\). Тогда \(x=\dfrac{3y\pm\sqrt{9y^2-8y^2}}{2}=\dfrac{3y\pm y}{2}\). Таким образом, первое уравнение раскладываем в уравнения двух прямых: \(x=y\) и \(x=2y \Leftrightarrow y=\dfrac{x}{2}\).
Во втором уравнение будем раскрывать модули. Если \(x>0\) и \(y>0\), то исходное уравнение равносильно такому: \(xy+xy=2 \Leftrightarrow xy=1\), что является гиперболой \(y=\dfrac{1}{x}\). Если одна из переменных раскрывает с изменением знака, а вторая без, то тогда получим \(0=2\), что неверно. И последний случай: если \(x<0\) и \(y<0\), то получаем \(xy=-1\),что является гиперболой во II и IV четвертях, однако мы рассматриваем III четверть. Поэтому исходное уравнение системы равносильно уравнению гиперболы \(y=\dfrac{1}{x}\), расположенной только в I четверти.
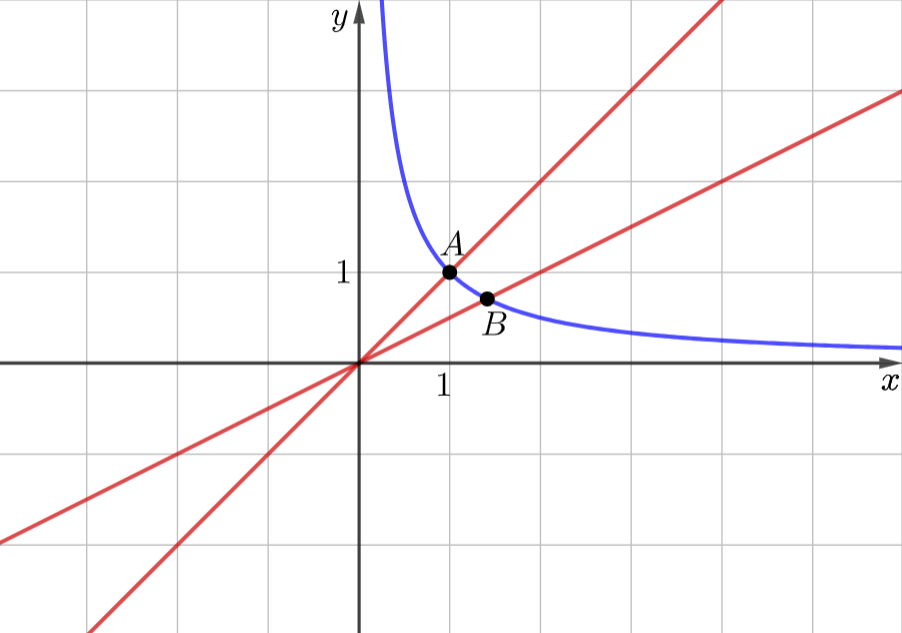
Далее строим графики и определяем одну из точек пересечения: \(A (1; 1)\). Подставляя её получаем верные равенства. Но точка \(B\) расположена не на пересечение клеток, поэтому не получится просто так определить её значение. Поэтому здесь придётся найти точку пересечения прямой \(y=\dfrac{x}{2}\) и гиперболы \(y=\dfrac{1}{x}\) алгебраически. Подставляем \(x=2y\) во второе уравнение, получаем \(y=\dfrac{1}{2y}\Leftrightarrow 2y^2=1 \Leftrightarrow y=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\). Здесь мы можем сразу отбросить отрицательное значение \(y\), так как знаем, что это точка в I четверти, в чём нам помог график. Находим соответствующий \(x=\sqrt{2}\).
Ответ: \((1 ; 1) ;\left(\sqrt{2} ; \dfrac{\sqrt{2}}{2}\right)\)
Пример 20.
Решите уравнение: \(|| x|-2|=\sqrt{4-x}\)
Если перед нами стоит задача решить уравнение, то мы можем преобразовать его в систему:
\(\left\{\begin{gathered}
y=||x|-2|\hfill\\
y=\sqrt{4-x}\hfill
\end{gathered}\right.\)
А теперь мы строим графики получившихся уравнений. Со вторым всё понятно. В первом будем раскрывать модули. Вначале рассмотрим \(x\geqslant0\), то есть \(y=|x-2|\). Если \(x\geqslant2\), то \(y=x-2\); если \(0\leqslant x <2\), то \(y=-x+2\). Теперь рассмотрим \(x<0\), то есть \(y=|-x-2|\). Если \(-2\leqslant x<0\), то \(y=x+2\); если \(x<-2\), то \(y=-x-2\).
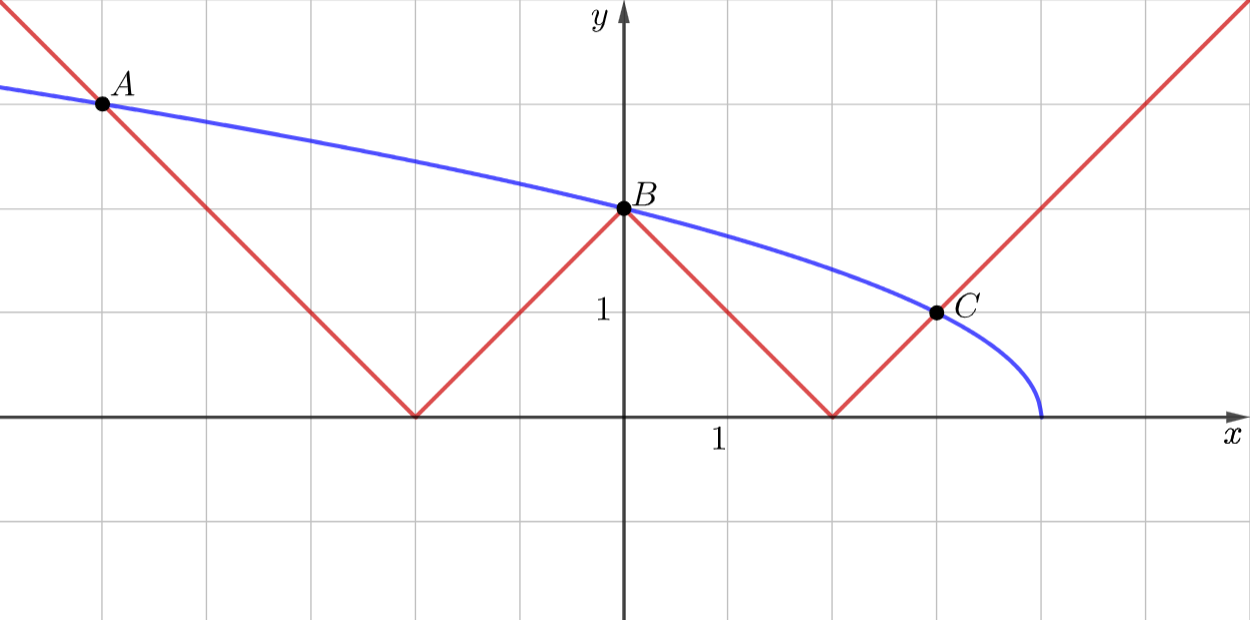
Таким образом, у нас получился график "корня" и ломаной. Они пересекаются в трёх точках. Так как у нас было именно уравнение, то нам нужны только значения \(x\).
Ответ: \(-5; 0; 3\)
Задачи для тренировки
Задача 18.
\(\left\{\begin{gathered}
x+y=-5\hfill\\
x y=4\hfill
\end{gathered}\right.\)
Задача 19.
\(\left\{\begin{gathered}
x^2+y^2=68\hfill\\
x y=16\hfill
\end{gathered}\right.\)
Задача 20.
\(\left\{\begin{gathered}
x^2-x y+x-y=0\hfill\\
x^2-y+1=0\hfill
\end{gathered}\right.\)
Задача 21. Решите уравнение \(2-x^2=\sqrt{x}\)
Задача 22.
\(\left\{\begin{gathered}
x^2=y+4|x|-4\hfill\\
y+3=|| x|-3|\hfill
\end{gathered}\right.\)
Подсказки к задачам для тренировки
Задача 6. Не забудьте проверить, является ли пара \((5; 8)\) решением системы
Задача 7. Сделайте замену \(\dfrac{1}{x-y}=a\) и \(x^2=b\)
Задача 8. Сделайте замену \(\dfrac{1}{2 x-y}=a\) и \(\dfrac{1}{2 x+y}=b\)
Задача 10. Разделите первое уравнение системы на второе и воспользуйтесь формулой суммы кубов
Задача 11. Умножьте первое уравнение системы на второй и решите иррациональное уравнение
Задача 14. Эта система не является однородной, однако первое уравнение в неё - однородное, начните с его решения
Задача 20. Первое уравнение системы разложите на множители
Задача 21. Преобразуйте уравнение в систему уравнений
Ответы к задачам для тренировки
Задача 1. \((2; 1)\)
Задача 2. \((-2; 3)\)
Задача 3. \((2; -3)\)
Задача 4. \((7; -2)\)
Задача 5. \((-3;-6), (5;2)\)
Задача 6. \((3,5; 8)\)
Задача 7. \((\sqrt{2}; \sqrt{2}+1), (-\sqrt{2} ; 1-\sqrt{2})\)
Задача 8. \((-1; 3)\)
Задача 9. \((0,5; 4)\)
Задача 10. \((8;0,5), (1;2)\)
Задача 11. \((5; 4)\)
Задача 12. \((1 ; 0), (-1 ; 0), (1 ; 1), (-1 ;-1) \)
Задача 13. \((2;1), (-2;-1),\) \(\left(-\frac{17}{\sqrt{39}}; \frac{1}{\sqrt{39}}\right),\) \(\left(\frac{17}{\sqrt{39}};-\frac{1}{\sqrt{39}}\right)\)
Задача 14. \((1 ;-1), (3 ;-3),\) \(\left(-13+\sqrt{157}; \dfrac{-13+\sqrt{157}}{2}\right),\) \(\left(-13-\sqrt{157}; \dfrac{-13-\sqrt{157}}{2}\right)\)
Задача 15. \((1;2), (2;1)\)
Задача 16. \((3;-2), (-2;3)\)
Задача 17. \((1 ; 3), (3 ; 1), (-1 ;-3), (-3 ;-1)\)
Задача 18. \((-4 ;-1), (-1 ;-4)\)
Задача 19. \((2 ; 8), (-2 ; 8), (2 ;-8), (-2 ;-8)\)
Задача 20. \((-1; 2)\)
Задача 21. \(x=1\)
Задача 22. Нет решений
