Как строить фигуры стереометрии
Как строить фигуры стереометрии
В данной статье мы разберём алгоритмы построения всех стереометрических фигур, которые могут встретиться на экзамене.
Призма
Начнём с определения: призма - это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани - параллелограммы
Разберём основные виды призм: треугольные, четырёхугольные, пятиугольные и шестиугольные. Конечно, их намного больше, однако они не встречаются на экзамене.
Также призма можем быть прямой и наклонной. У прямой призмы боковые рёбра перпендикулярны её основаниям. У наклонной призмы боковые рёбра наклонены в плоскостям оснований под равными углами.
Прямая призма называется правильной, если у неё в основаниях правильные многоугольники (то есть равносторонний треугольник, квадрат, правильный пятиугольник и так далее). Получается, что правильная призма - эта та призма, у которой в основаниях правильные многоугольники, а боковые грани - прямоугольники
Треугольная призма
Если в основании треугольник, то лучше всего рисовать тупоугольный не равнобедренный треугольник, вне зависимости от того, какой должен быть в основание. Именно так будут лучше всего видны все элементы призмы.
Шаг 1. Итак, строим один из таких треугольников.

Шаг 2. Далее разберём алгоритм построения прямой призмы. Для этого из всех вершин основания проводим вертикальные отрезки равной длины - боковые рёбра.

Шаг 3. Дальше соединяем концы вертикальных отрезков и получаем верхнее основание, равное нижнему.

Шаг 4. Рёбра, которые мы не видим, нужно изобразить пунктиром на чертеже. Лучше всего сразу представлять себе будущую фигуру и чертить данные рёбра пунктиром изначально.

Если призма не прямая, а наклонная, то после построения нижнего основания (шаг 1) надо строить не вертикальные отрезки, а наклонённые к нижнему основанию под одинаковым углом. При этом все они должны быть параллельны друг другу и иметь равную длину.
Далее проводим отрезки, образующие верхнее основание (шаг 3), а невидимые линии изображаем пунктиром (шаг 4).

Таким образом, мы получили прямую треугольную и наклонную треугольную призмы.
Посмотрим, как это будет выглядеть со вторым треугольником.
Шаг 1. 
Шаг 2. 
Шаг 3. 
Шаг 4. 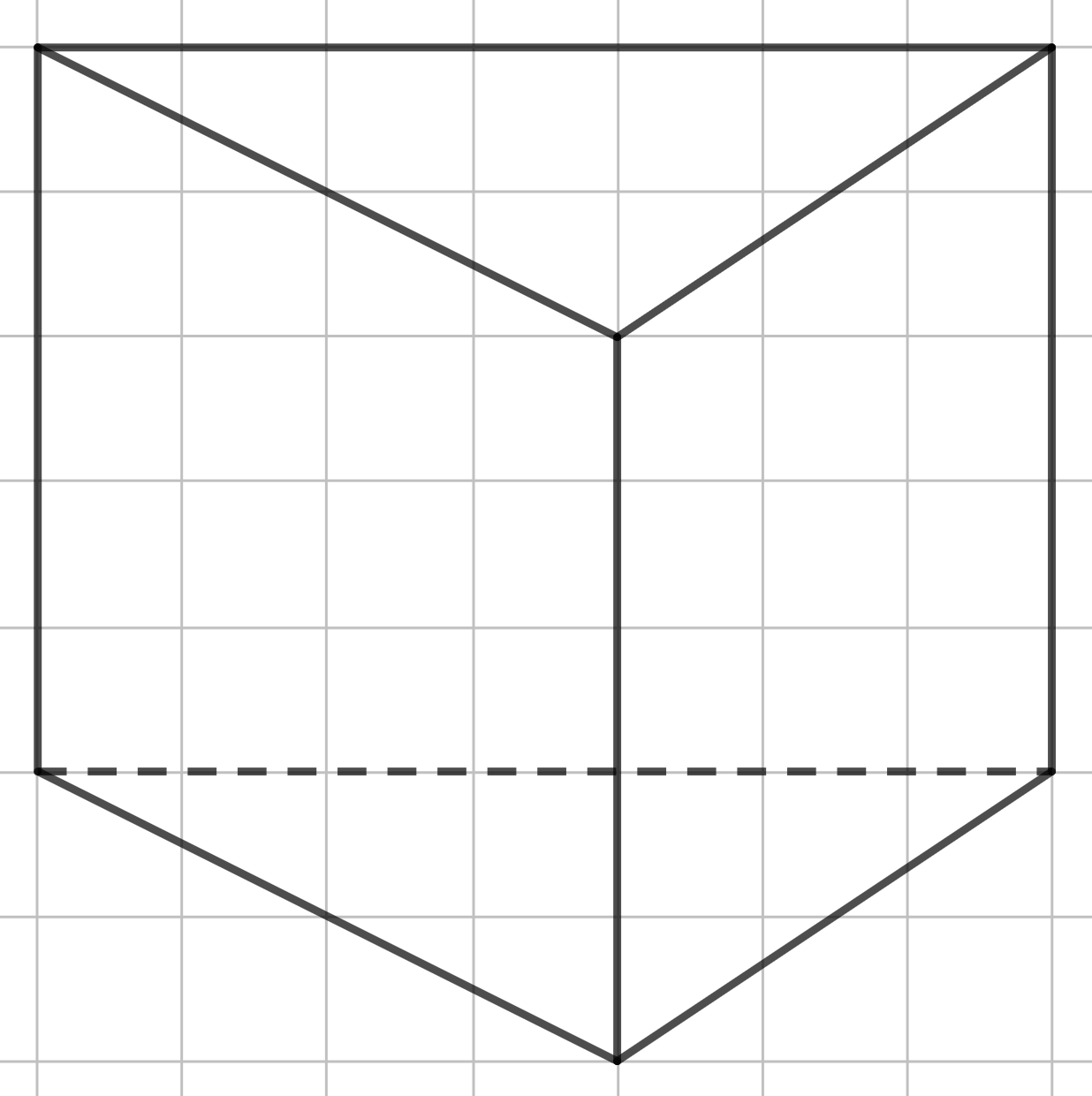
И, аналогично алгоритму, строим наклонную призму. В итоге получаем такую фигуру.

Четырёхугольная призма
Если в основание призмы лежит параллелограмм, прямоугольник или квадрат, то чертим параллелограмм. Дело в том, что если начертить прямоугольник или квадрат, то боковые рёбра будут накладываться друг на друга, и чертежа не получится. А чтобы диагональ призмы не наложилась на сторону основания, нужно, чтобы величина острого угла параллелограмма в основании было примерно \(30^{\circ}\).
Шаг 1. 
Шаг 2. Итак, после построения нижнего основания необходимо провести равные вертикальные отрезки, которые являются боковыми рёбрами.

Шаг 3. Далее соединяем концы этих отрезков и получаем верхнее основание.

Шаг 4. Последним шагом невидимые линии изображаем пунктиром. Прямая четырёхугольная призма, которую также называют параллелепипедом, готова!

Если же нужно было построить наклонную призму, то вместо вертикальных боковых рёбер чертим равные наклонные линии. В итоге получаем такой результат.

Построения всех призм очень похоже: строим нижнее основание (шаг 1), проводим боковые рёбра (шаг 2) и, соединив их концы, получаем верхнее основание (шаг 3). А затем невидимые рёбра изображаем пунктиром (шаг 4).
Разберём случай, когда в основание призмы находится квадрат. Однако на рисунке мы строим параллелограмм.
Шаг 1. 
Шаг 2. 
Шаг 3. 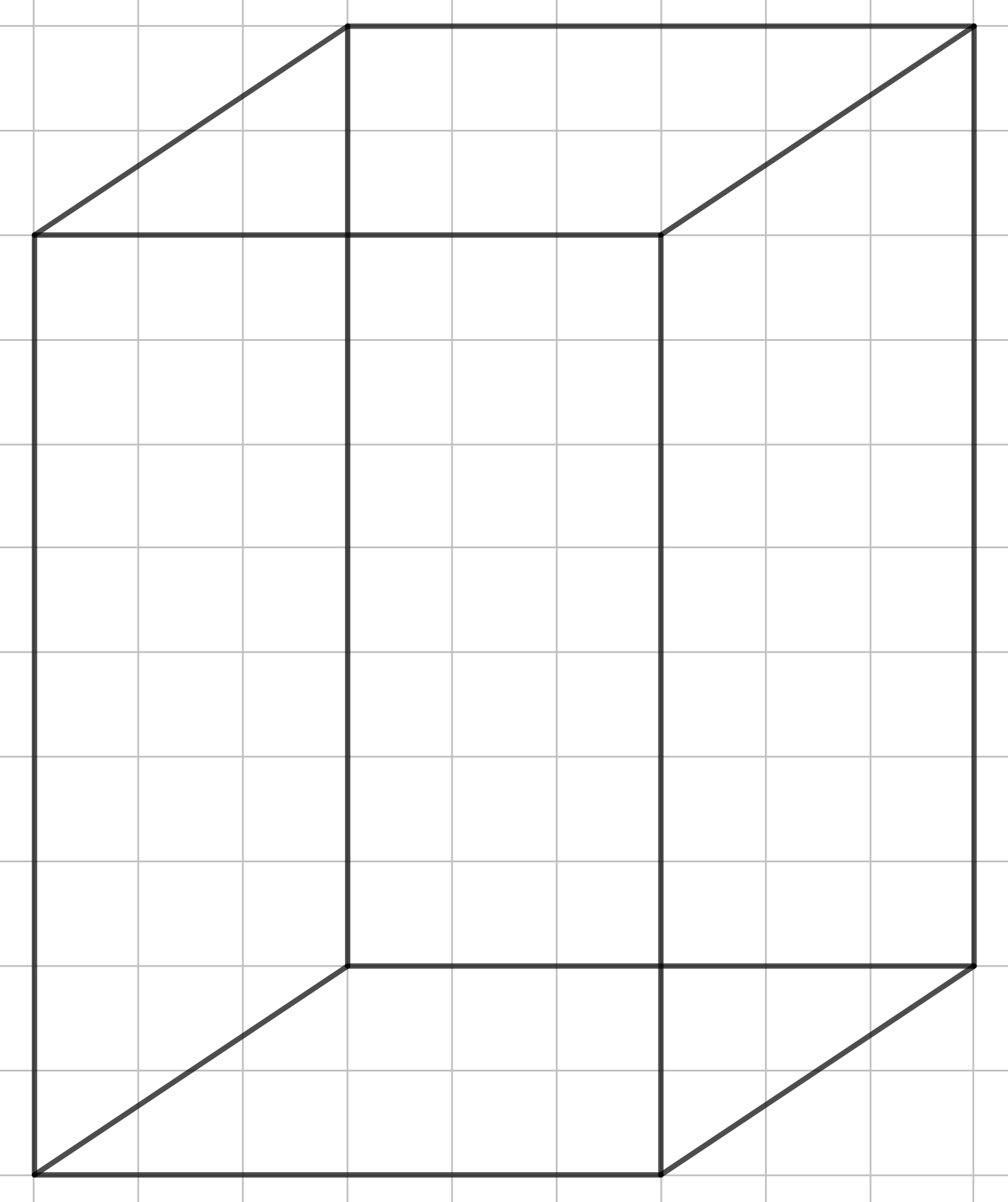
Шаг 4. 
Таким образом, мы получили прямой параллелепипед с квадратом в основание. А так выглядит он же, только наклонный.

Стоит ещё рассмотреть случай, когда в основание другой четырёхугольник. Например, трапеция. Здесь самое главное не делать её равнобедренной, даже если таково условие задачи. Постарайтесь сделать одну боковую сторону больше другой, а острый угол - поострее.
Шаг 1. 
Дальнейший алгоритм совпадает с предыдущими построениями. И мы получили такую призму.
Шаг 2. 
Шаг 3. 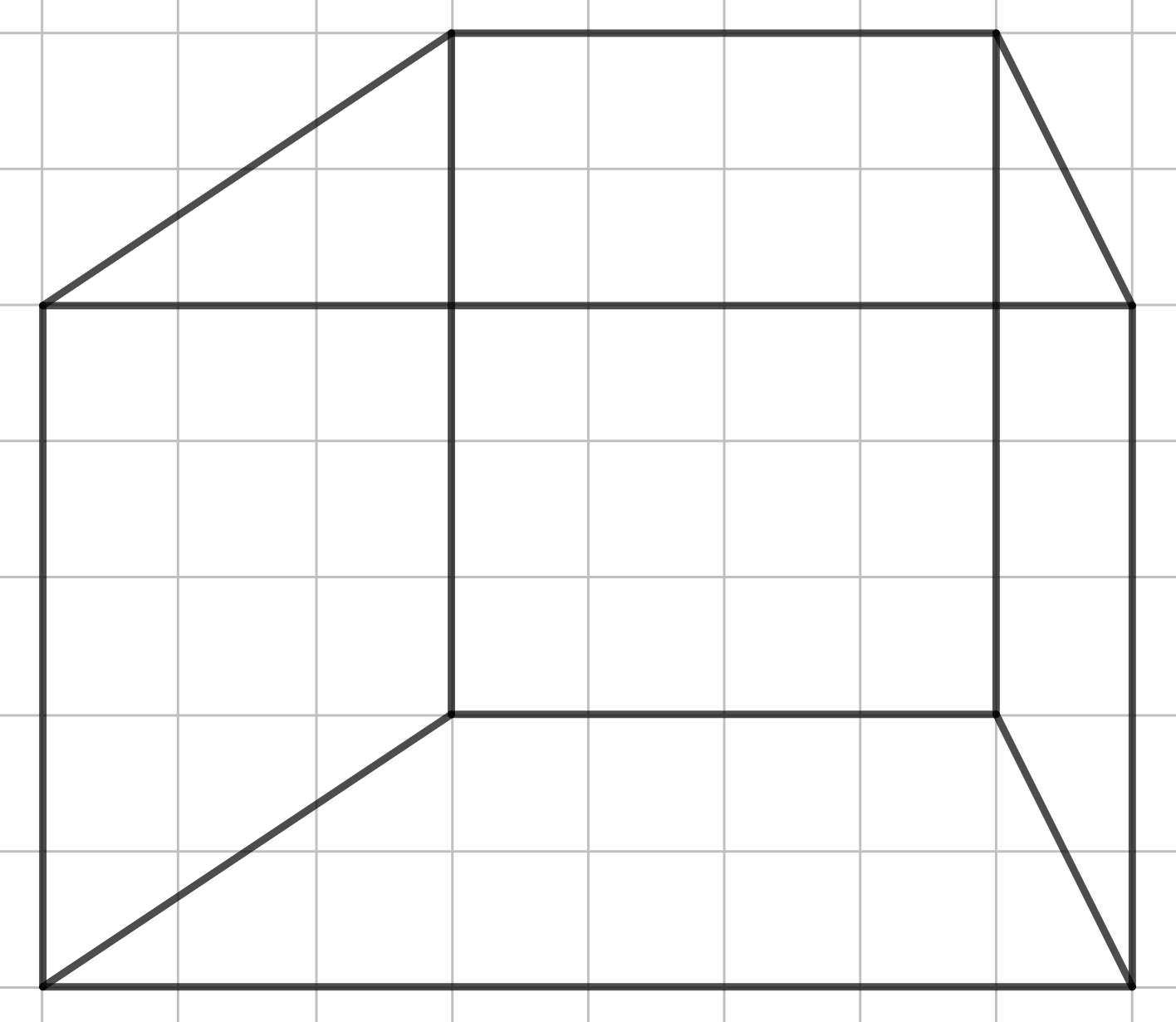
Шаг 4. 
И её наклонный вариант выглядит так.

Последнее, что нам нужно разобрать в этом разделе - куб. Куб - это правильная призма, каждая грань которого является квадратом. Первым делом строим параллелограмм в основание.
Шаг 1. 
Шаг 2. Дальше нам нужно провести боковые рёбра. И в случае куба важно, чтобы боковое ребро было равно длинной стороне параллелограмма. В данном случае это та сторона, которая ближе к нам. Поэтому боковое ребро, как и наибольшую сторону параллелограмма, поднимаем вверх ровно на 6 клеток. Делаем также со всеми боковыми рёбрами.
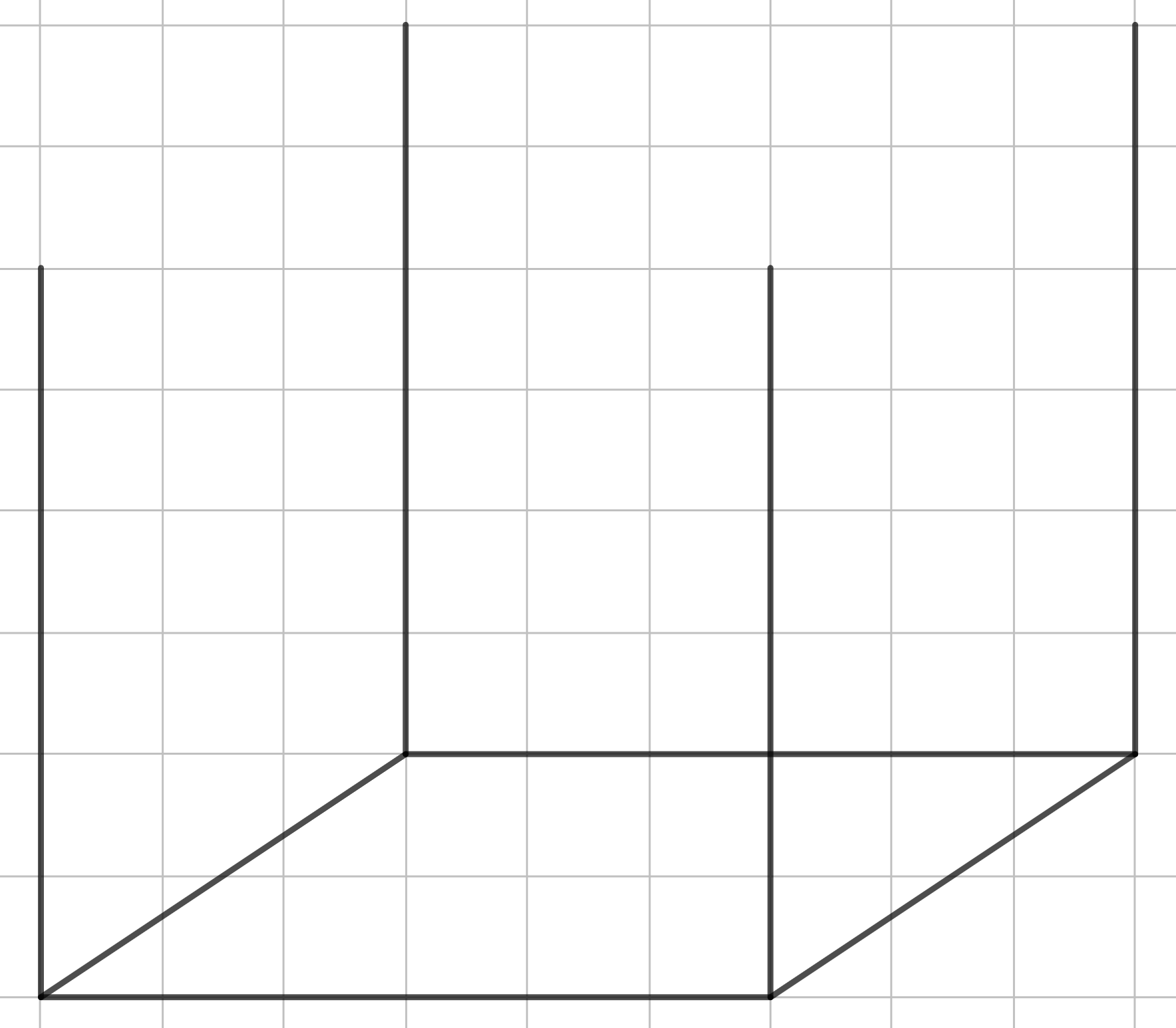
Далее все просто: строим верхнее основание и преобразуем невидимые линии. Получили куб!
Шаг 3. 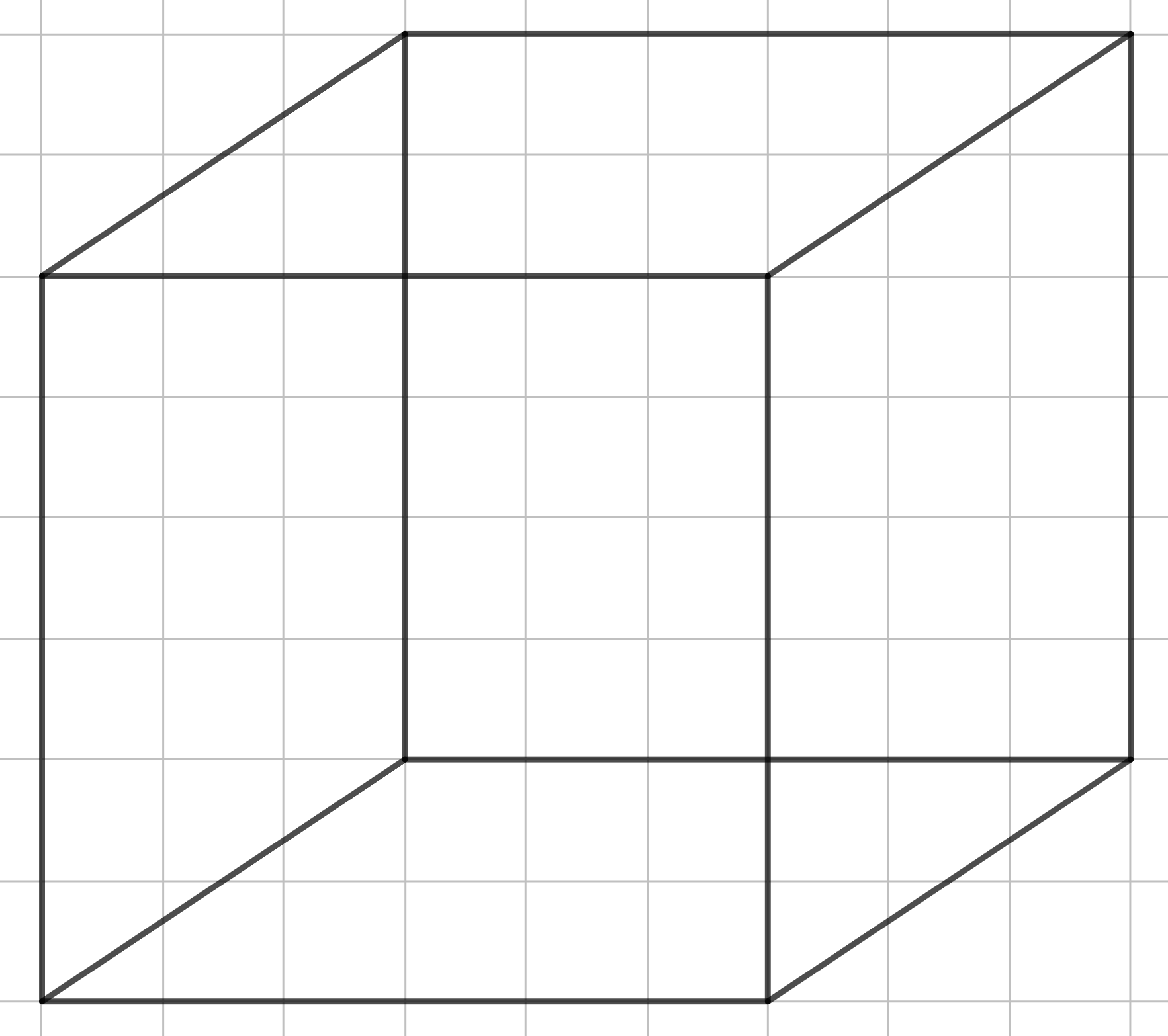
Шаг 4. 
Очевидно, что куб не может быть наклонным, ведь по определению это прямая призма. Иначе в боковых гранях никак не получатся квадраты.
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Пятиугольная призма
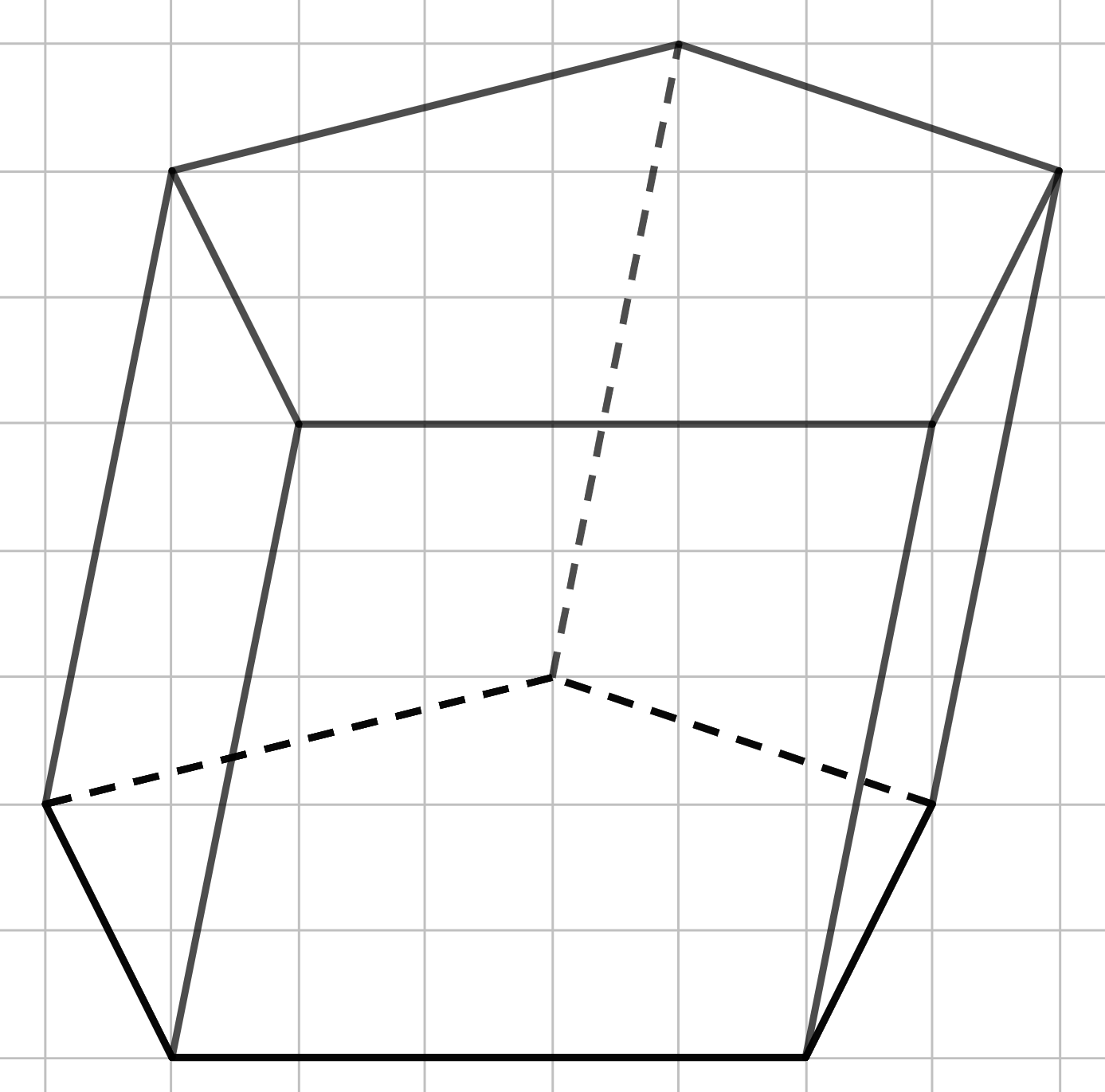
Если в основание призмы лежим пятиугольник (будь он правильный или нет), то строим такой вот пятиугольник. Такие длины сторон очень удобны, ведь так боковые рёбра не будут накладываться друг на друга.
Шаг 1. 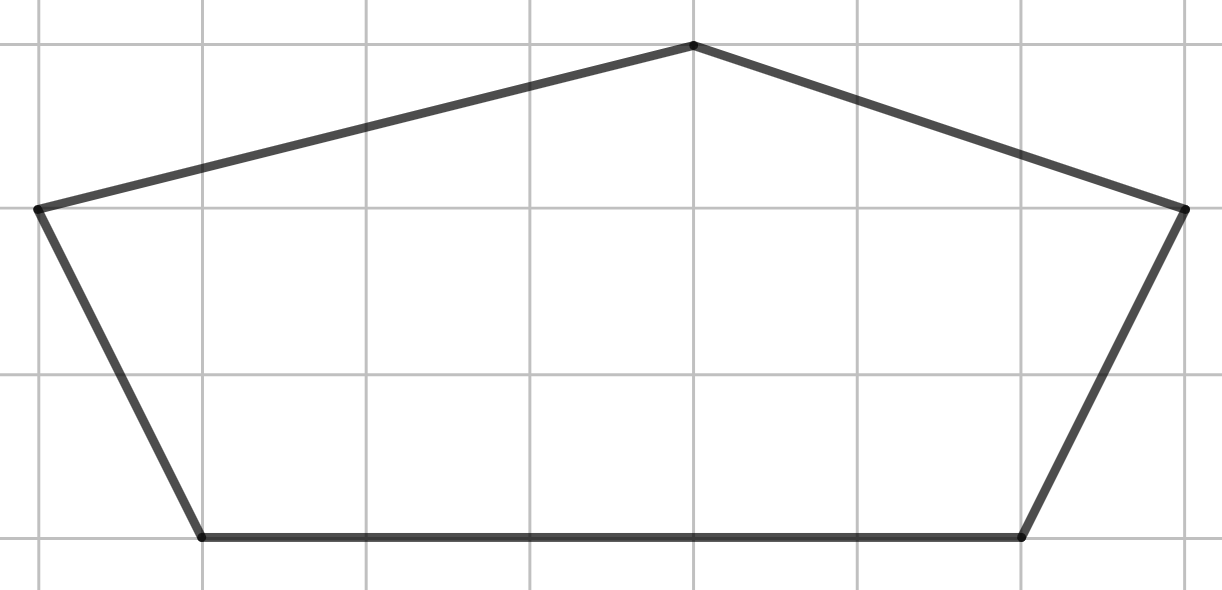
А дальнейшее построение уже должно быть понятно. Проводим равные вертикальные отрезки, являющиеся боковыми рёбрами. Затем строим верхнее основание и пунктиром изображаем те рёбра, которые мы не видим, если смотрим на фигуру.
Шаг 2. 
Шаг 3. 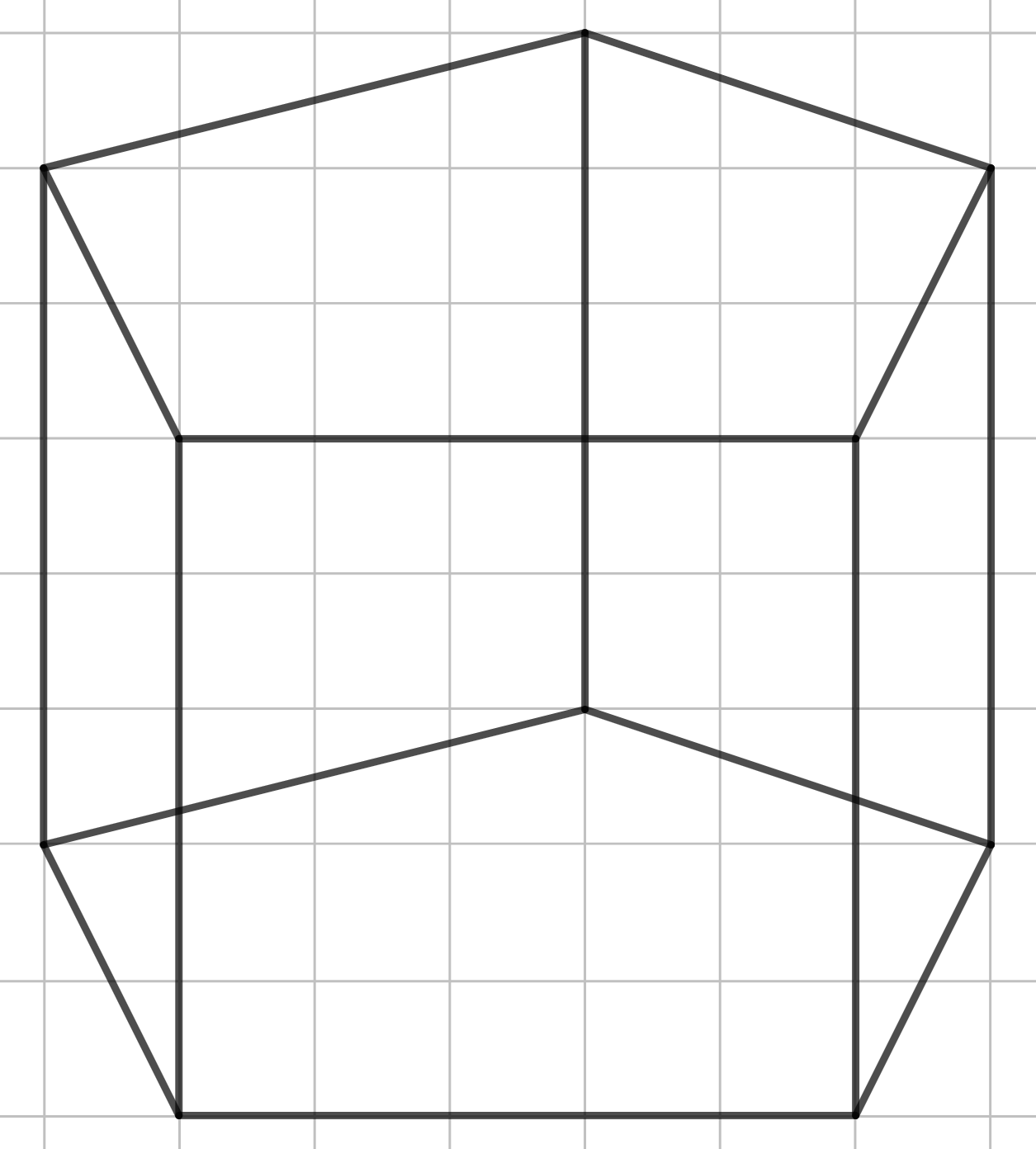
Шаг 4. 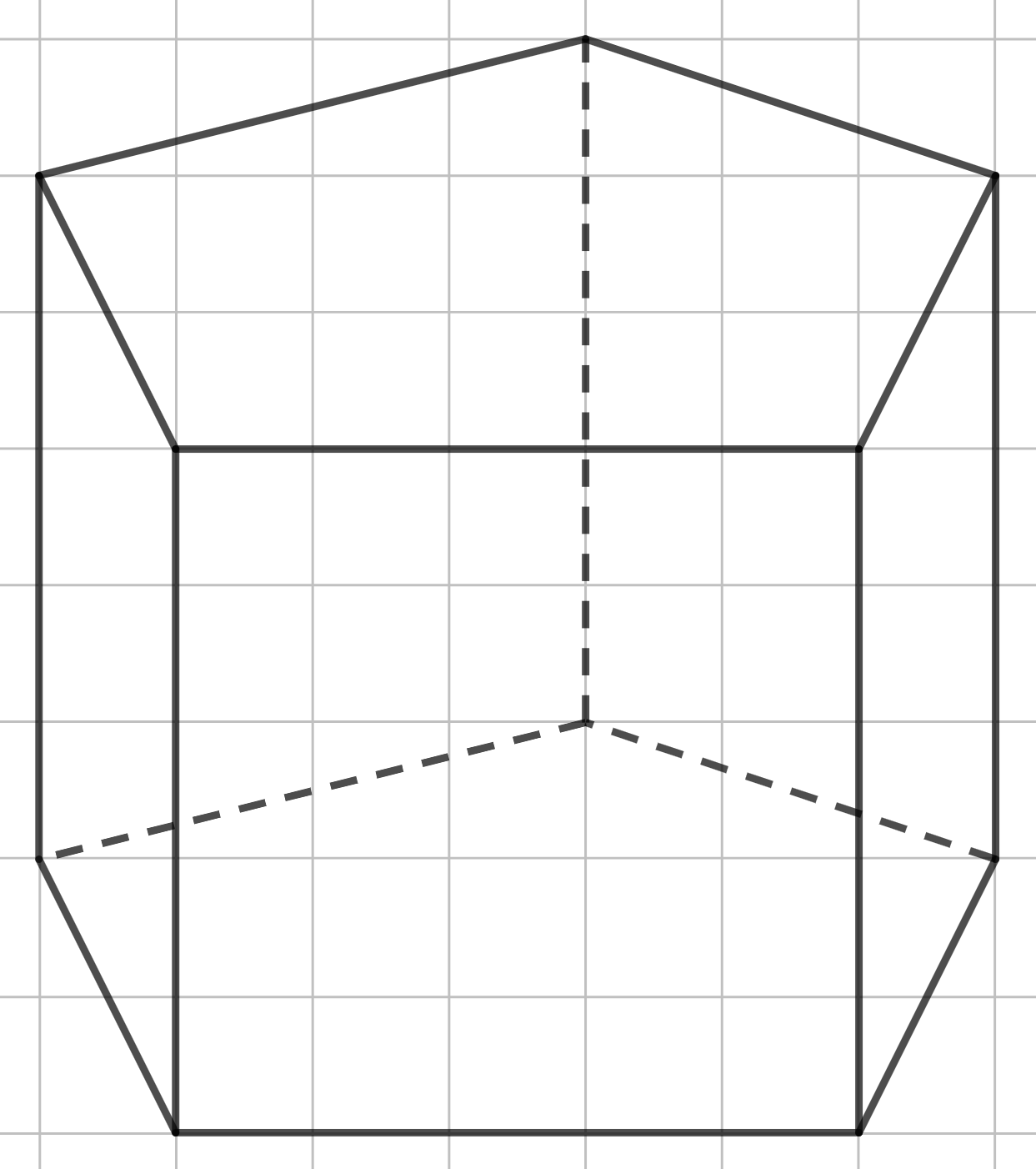
И данную призму можно построить наклонной. Она будет выглядеть так.
Шестиугольная призма
Здесь, как и в предыдущем построение, в основание нужно начертить шестиугольник, который не является правильным. Делать это лучше всего по данному образцу. Именно точно такого же количества клеток стоит придерживаться, чтобы итоговая фигура получилась красивой, а все построения на ней - видны и ясны. Не забываем следить, чтобы противоположенные стороны шестиугольника были параллельны.
Шаг 1. 
Далее просто строим фигуру по алгоритму.
Шаг 2. 
Шаг 3. 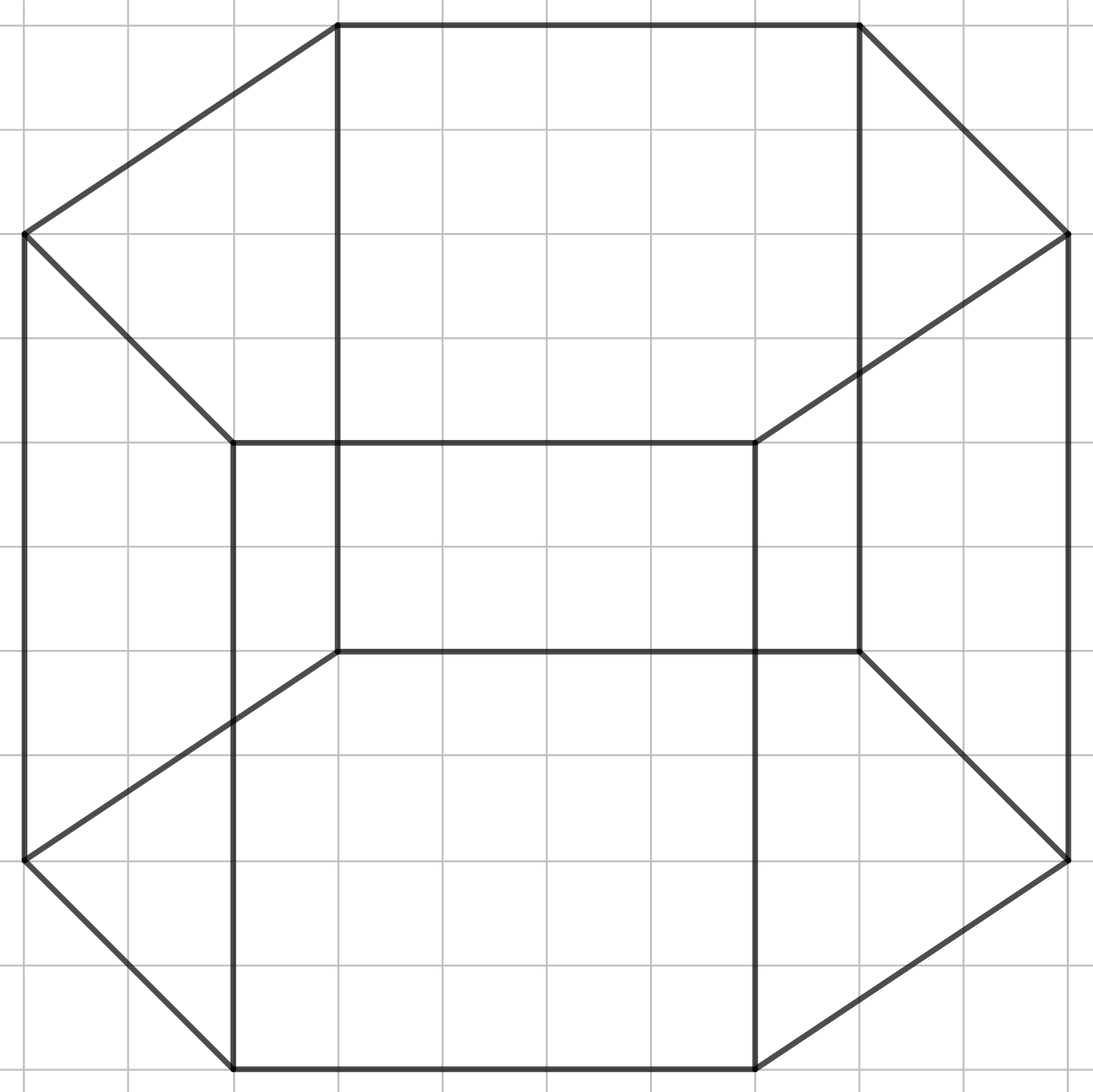
Шаг 4. 
И также наклонная призма, построение которое уже не должно вызывать труда.

Таким образом, мы прошлись по всем основным видам призм. Алгоритм построения везде один. Самое главное - это верно построить фигуру в основание призмы. Она не должна быть правильной (даже если это условие задачи), треугольник и трапеция не должны быть равнобедренными, а квадрат должен быть параллелограммом. В этом случае чертёж получится замечательным.
Пирамида
Также вначале разберём определение: пирамида - это многогранник, основанием которого является многоугольник, а остальные грани являются треугольниками с общей вершиной, которую называют вершиной пирамиды.
Пирамида называется правильной, если в основание лежит правильный многоугольник (равносторонний треугольник, квадрат или любой другой правильный \(n\)-угольник), и основание высоты совпадает с центром этого многоугольника.
Пирамиды также подразделяются на типы в зависимости от фигуры в основание. Разберём те же самые основные фигуры.
Треугольная пирамида
Шаг 1. В основание треугольной пирамиды лежит треугольник. И, независимо от его типа, как и при построение призмы, чертим не равнобедренный тупоугольный треугольник.
Дальше нам нужно отметить центр фигуры (или же центр масс), лежащей в основание. Эта точка - проекция вершины пирамиды на нижнее основание. Для любого треугольник такой точкой является точка пересечения медиан. Поэтому проводим две медианы (третью проводить не обязательно, ведь мы уже получили их точку пересечения).

Шаг 2. Далее из этой точки, то есть из центра основания, проводим вертикальную линию и ставим на неё точку. Она будет являться вершиной пирамиды.
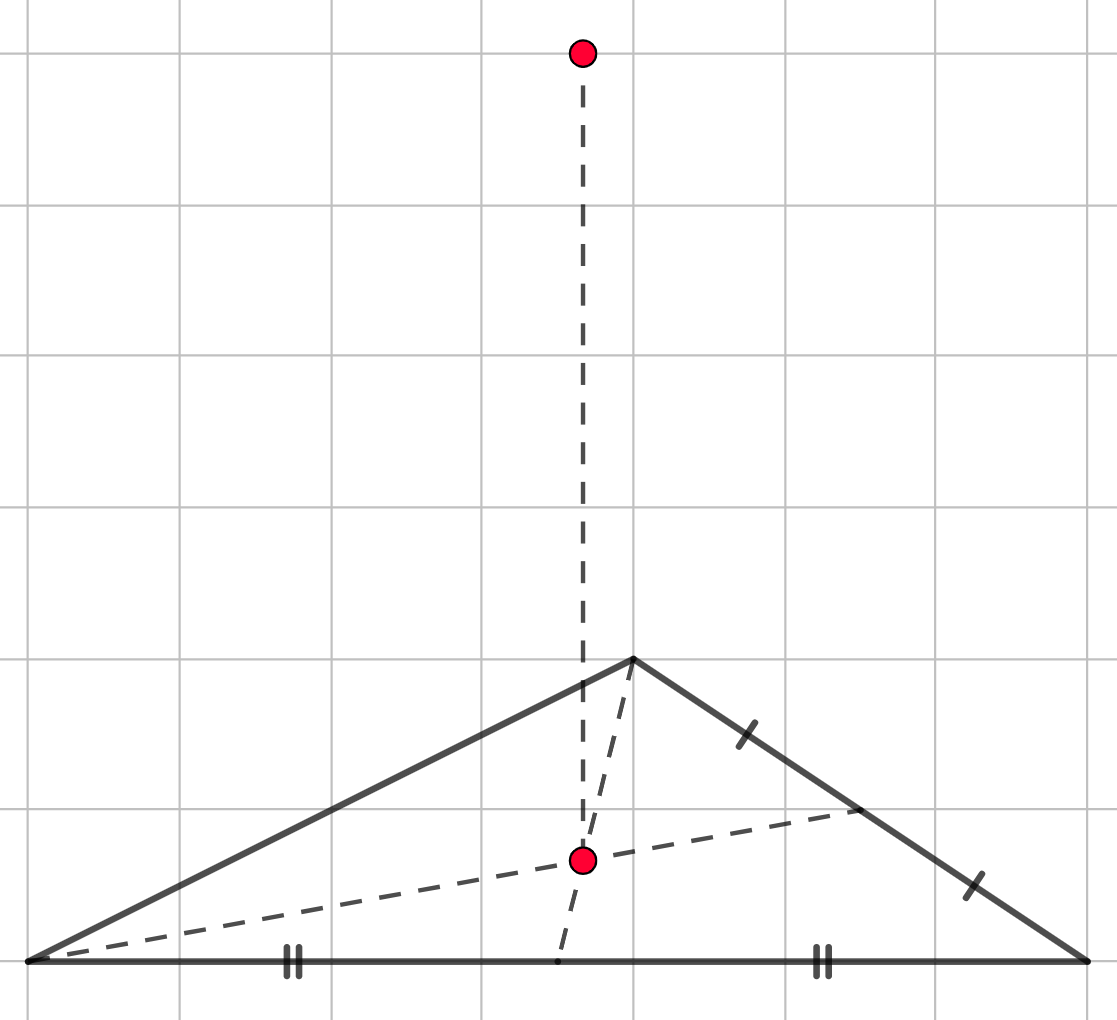
Шаг 3. Следом нам нужно соединить вершину пирамиды со всеми вершинами основания.

Шаг 4. А невидимые рёбра изображаем пунктиром. Теперь мы получили четырёхугольную пирамиду!
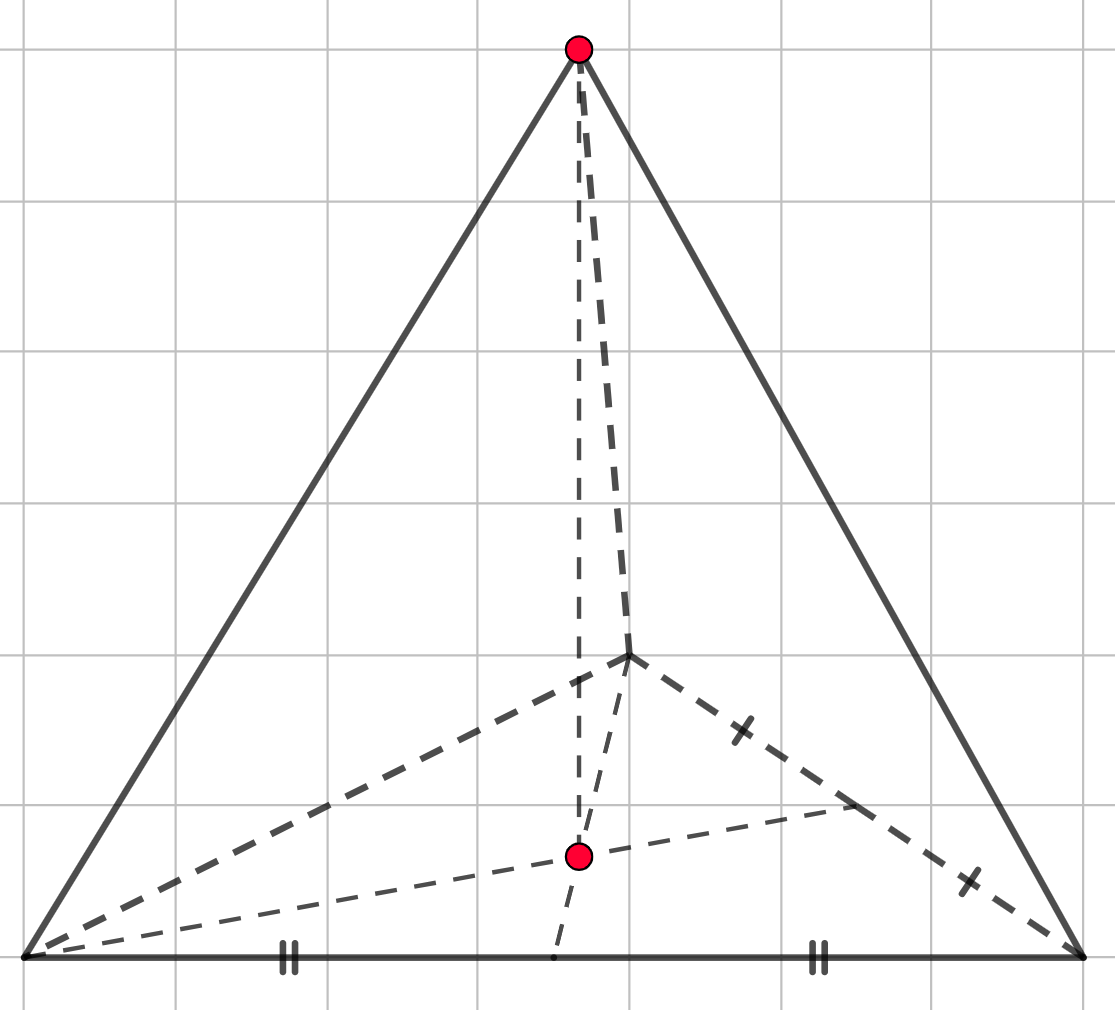
Рассмотрим построение треугольной пирамиды с другим треугольником в основание.
Шаг 1. 
Шаг 2. 
Шаг 3. 
Шаг 4. 
Вспомним, что если у треугольной пирамиды в основание лежит равносторонний треугольник и боковые рёбра равны между собой, то она является правильной треугольной пирамидой. А если окажется так, что её боковое ребро равно ребру основания, то такая фигура называется правильным тетраэдром и состоит из четырёх равносторонних треугольников.
Четырёхугольная пирамида
Основание по-прежнему является параллелограмм. Чтобы найти его центр, нужно провести обе диагонали. Их точка пересечения и есть проекция вершины пирамиды на нижнее основание.
Шаг 1. 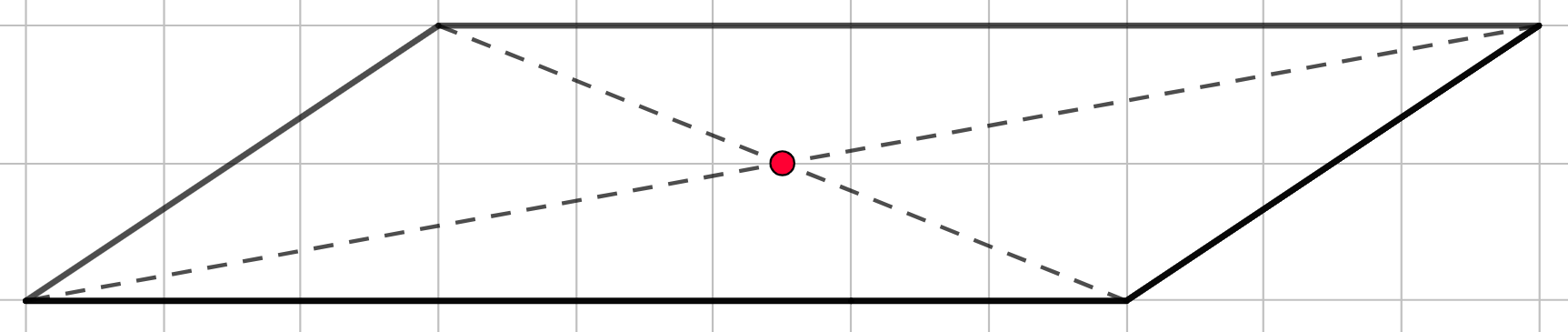
Шаг 2. Далее проводим вертикальный отрезок из центра основания, который оканчивается в вершине пирамиды.
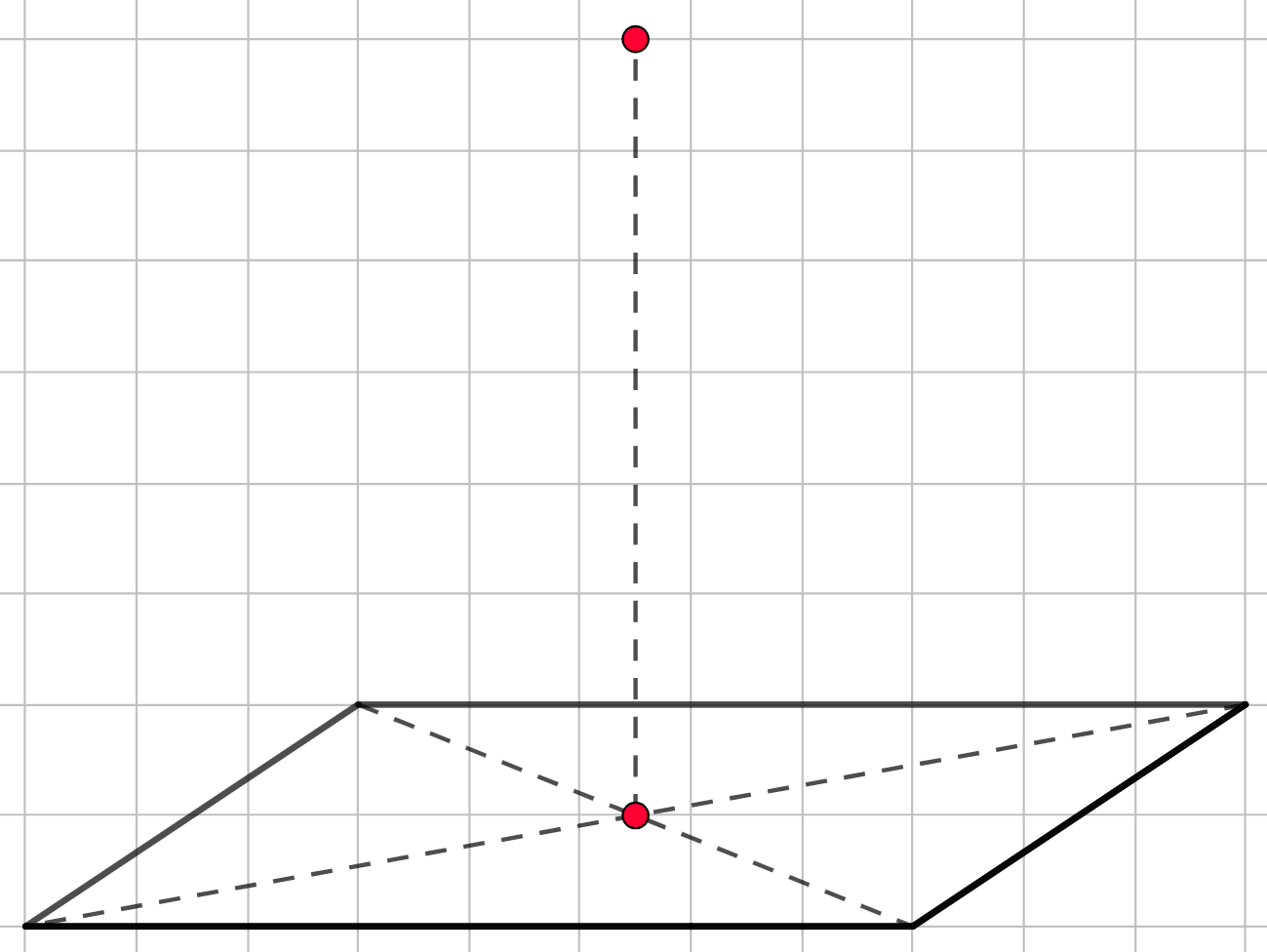
Шаг 3. Из вершины пирамиды проводим четыре отрезка к вершинам нижнего основания.
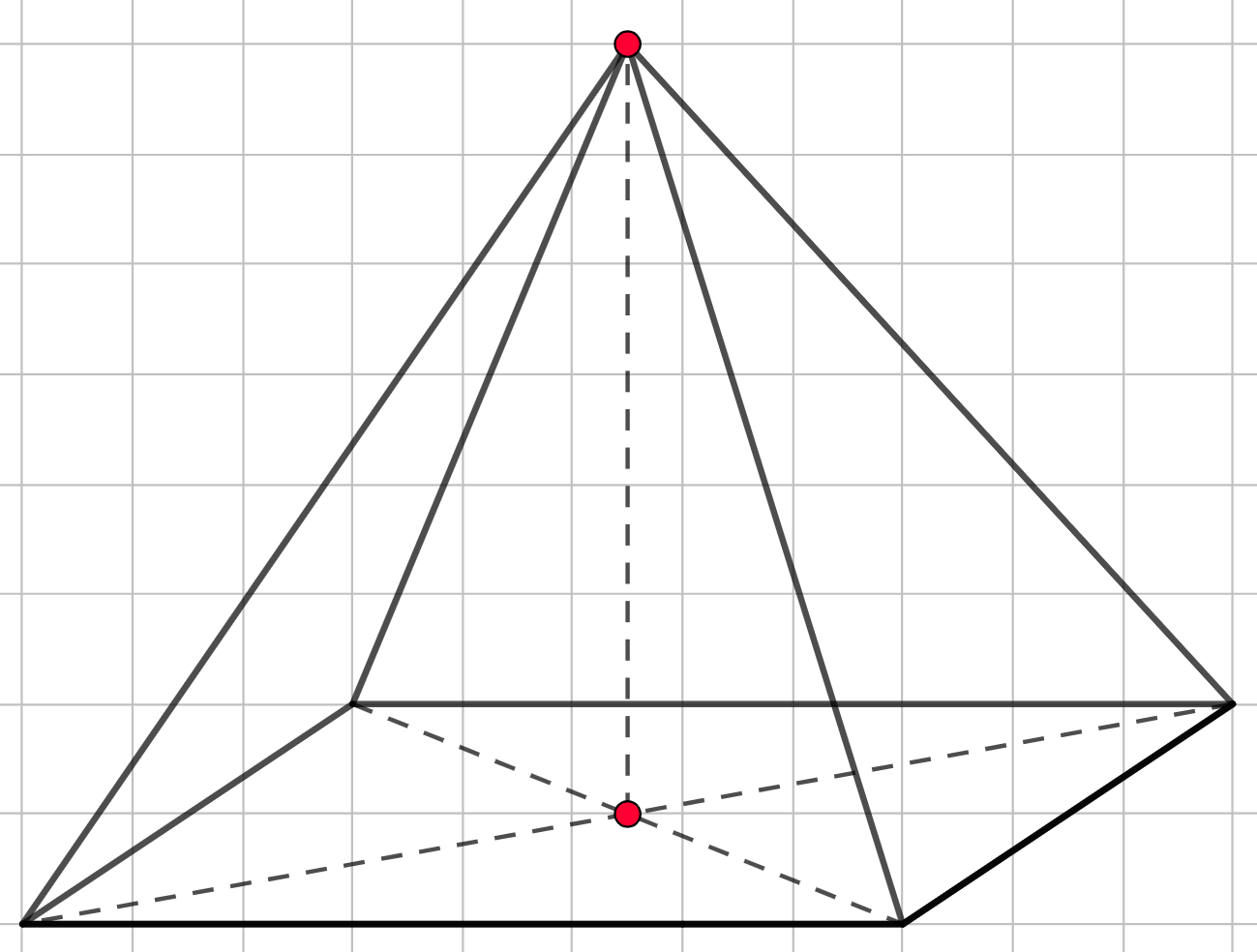
Шаг 4. Последним шагом невидимые линии изображаем пунктиров. Теперь пирамида готова!

Теперь разберём случай, когда в основание находится трапеции. У неё уже нельзя точно определить центр, поэтому находим его примерное расположение.
Шаг 1. 
Далее действуем по алгоритму: проводим отрезок до вершины пирамиды (шаг 2), а далее проводим все боковые рёбра (шаг 3). Невидимые рёбра отмечаем пунктиром (шаг 4).
Шаг 2. 
Шаг 3. 
Шаг 4. 
Пятиугольная и шестиугольная пирамиды
Здесь всё предельно ясно. То, как строить фигуры, лежащие в нижнем основание, мы уже разобрали ранее. Здесь строим их по тем образцам, чтобы избежать наложения линий. А дальнейшие построения аналогичны и изображены ниже.
Пятиугольная пирамида
Шаг 1. 
Шаг 2. 
Шаг 3. 
Шаг 4. 
Шестиугольная пирамида
Шаг 1. 
Шаг 2. 
Шаг 3. 
Шаг 4. 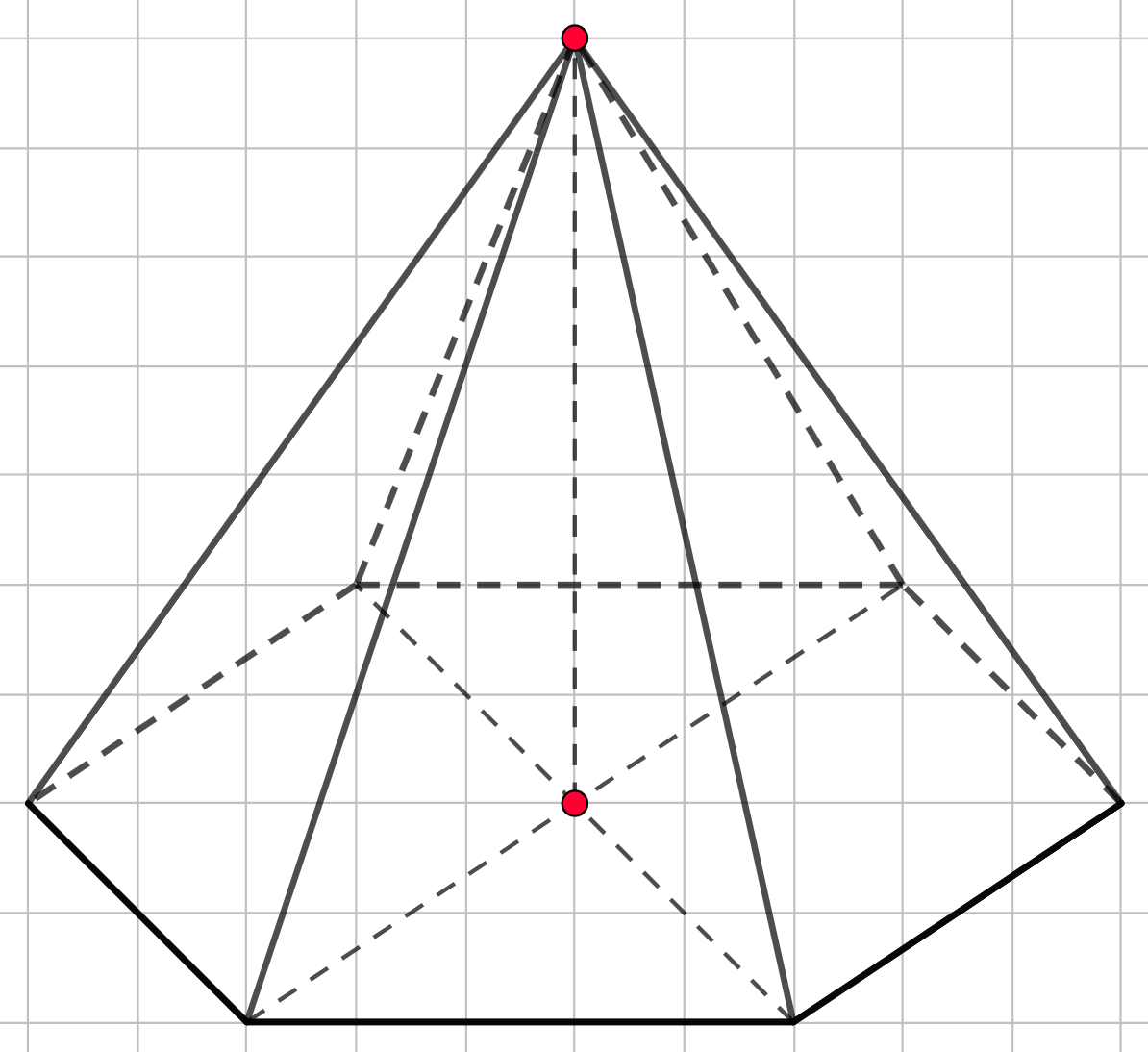
Теперь мы умеем строить все необходимые виды пирамид.
Тело вращения
По определению это объёмная фигура, полученная при вращение геометрической фигуры, вокруг оси, лежащей в той же плоскости. К телам вращения в школьной геометрии относят цилиндр, конус и шар. По очереди разберём их построения.
Цилиндр
Цилиндр - это тело, которое описывает прямоугольник при вращение вокруг одной из его сторон. Верхний и нижний круги - это основания цилиндра. Прямая, проходящая через центры кругов - ось цилиндра. Отрезок, параллельный оси цилиндра, концы которого лежат на двух основания - это образующая цилиндра.
В целом, цилиндр похож на призму, ведь он также имеет два параллельных основания, соединённых отрезками.
Шаг 1. Чтобы построить цилиндр, вначале начертим его нижнее основание. Несмотря на то, что оно является кругом, мы чертим эллипс.
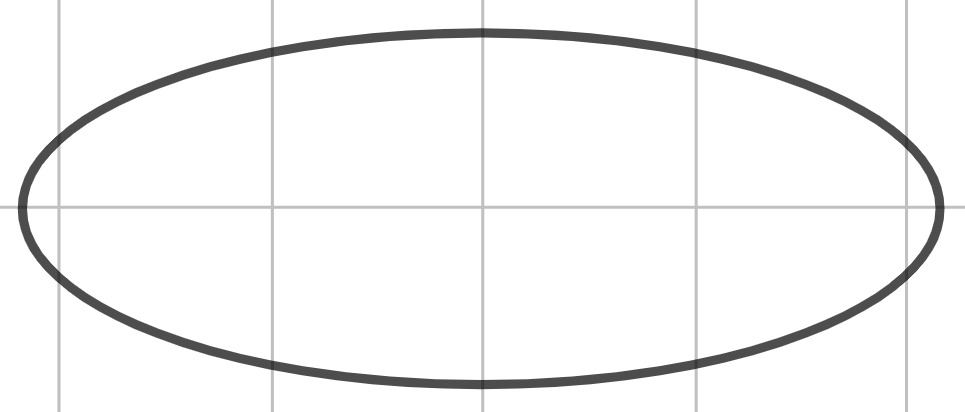
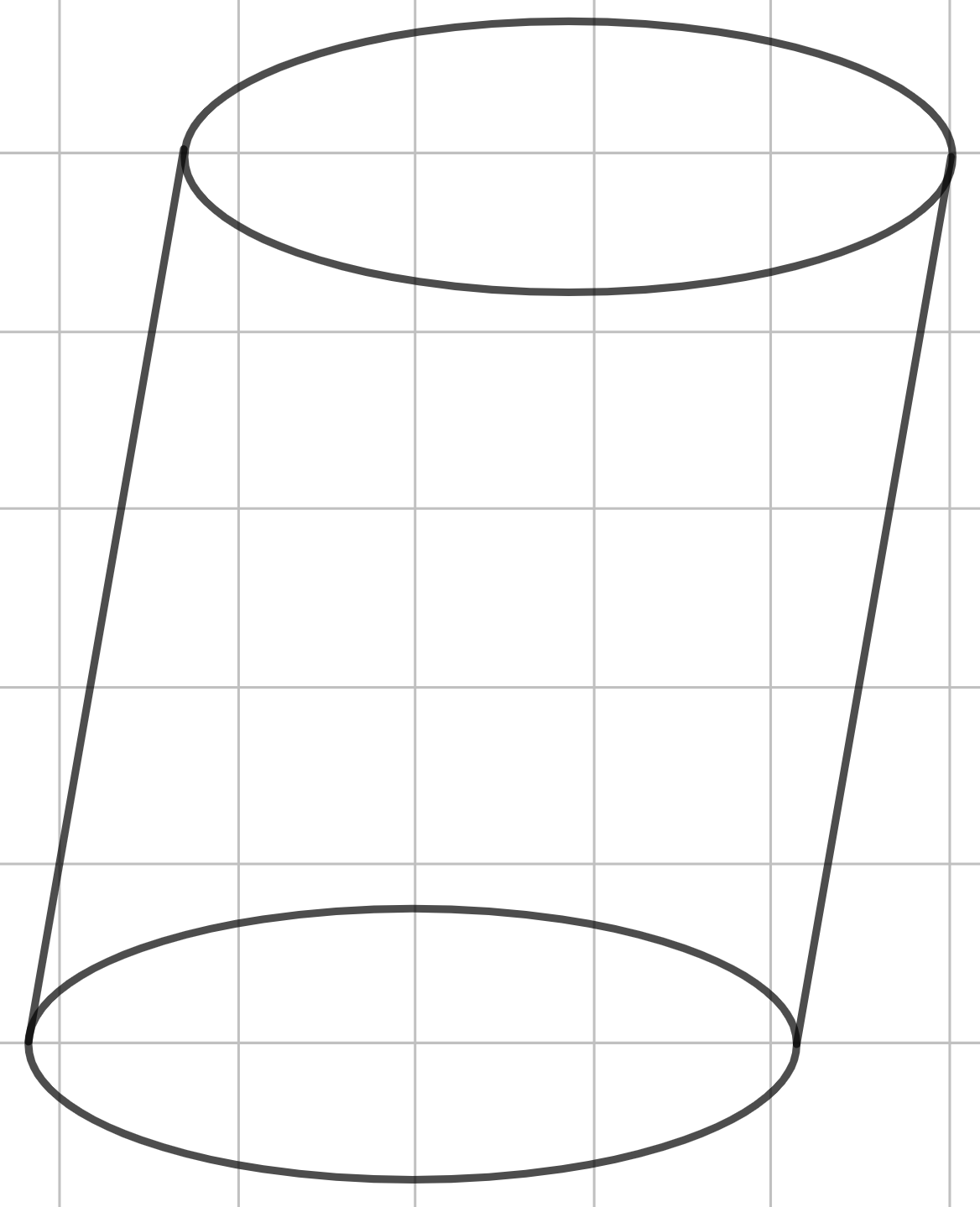
Шаг 2. Для построения прямого цилиндра проводим два вертикальных отрезка из двух диаметрально противоположенных точек нижнего основания (вернее, конечно, это называть касательными к окружности, лежащей в нижнем основание).

Шаг 3. Далее в верхнем основание строим круг, который совпадает с кругом в нижнем основание. Тем самым мы получили прямой цилиндр.

Но цилиндр, как и призма, может быть наклонным. Для этого образующие будем проводить не вертикально, а под наклоном. Главное, чтобы они были параллельны и равны. Основания цилиндра также будут равны и параллельны. Так должен выглядеть наклонный цилиндр
Конус
Конус - это тело, которое описывает прямоугольный треугольник при вращение вокруг одного из его катетов. Данный катет является осью конуса, а другой - радиусом. Гипотенуза же будет образующей конуса.
Шаг 1. По построению конус будет схож с пирамидой. Для этого вначале начертим его основание - эллипс.
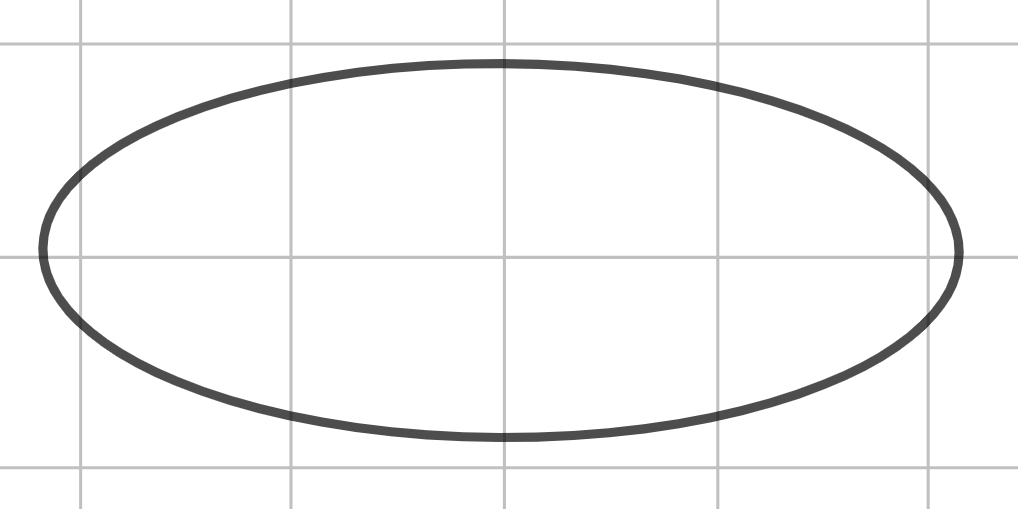
Шаг 2. Далее из центра основания (то есть из центра эллипса) проводим вертикальный отрезок. Оканчивается он в вершине конуса.
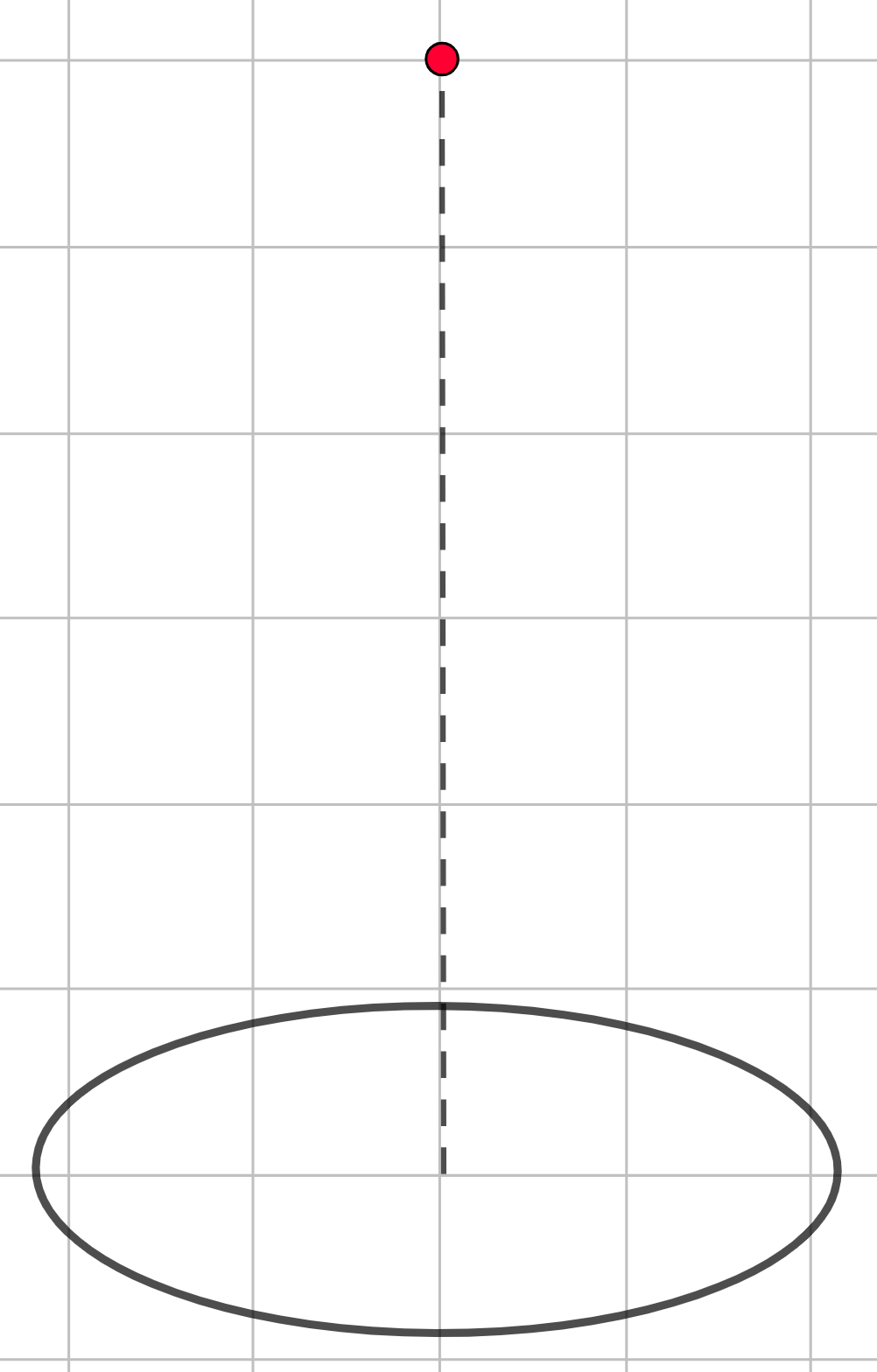
Шаг 3. И следом проводим образующие - отрезки, соединяющие вершину конуса с точками на основание. Здесь удобно, как и у цилиндра, провести две линии, концы которых лежат на диаметре основания.

Шар
Шар - это тело, которое описывает полукруг при вращение вокруг своего диаметра.
Шаг 1. Его построение достаточно просто. Сначала чертим эллипс - он будет являться большим кругом нашего шара (большой круг - это сечение шара, проходящее через его центр)
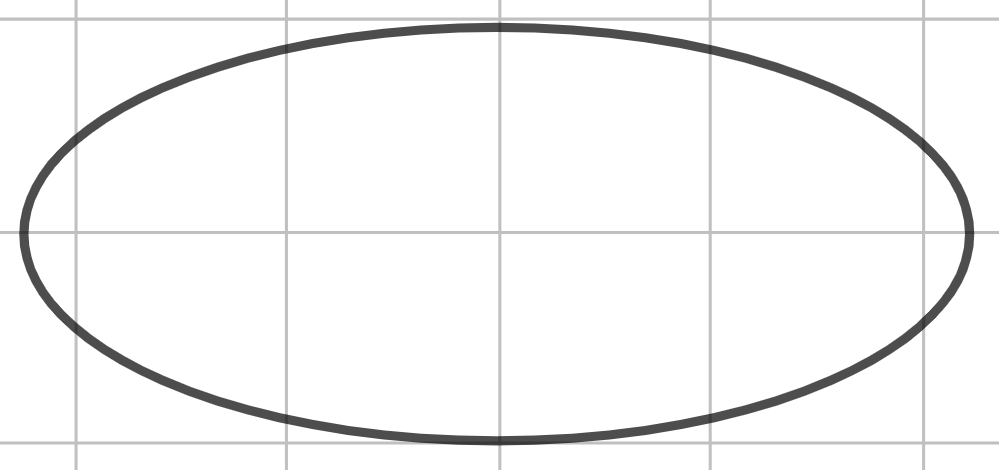
Шаг 2. Далее через две диаметрально противоположенные точки получившегося эллипса проводим окружность, центр которой совпадает в центром эллипса. Так мы получили шар

