8 задание ЕГЭ профиль. Производная
Производная. 8 задание ЕГЭ по математике
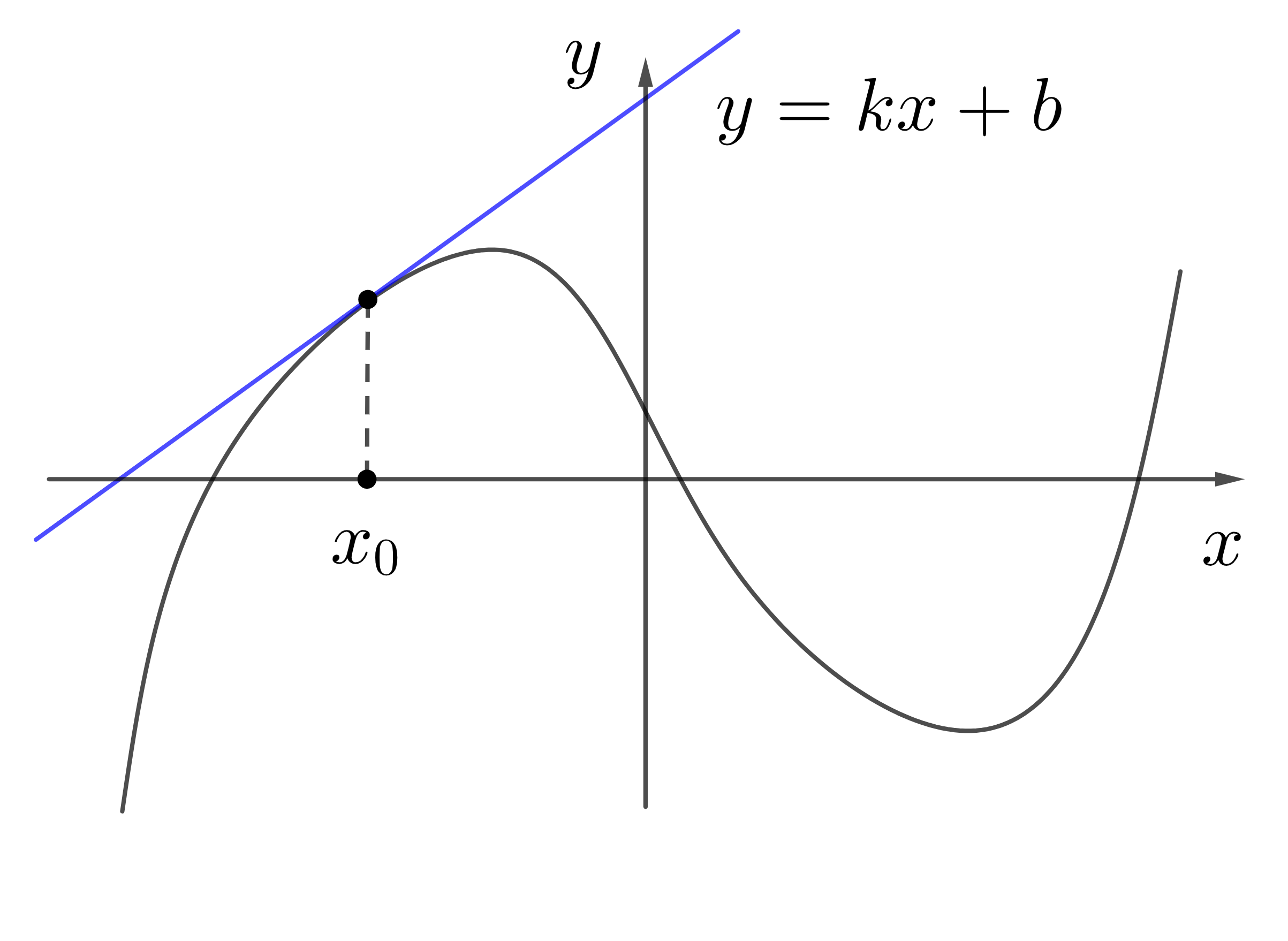
Производная - коэффициент наклона касательной
Чтобы найти значение производной функции в любой точке, нужно найти коэффициент наклона касательной \(k\).
\(f^{\prime}\left(x_0\right)=k=\operatorname{tg} \alpha\).
\(\alpha\) - угол с осью \(x\)
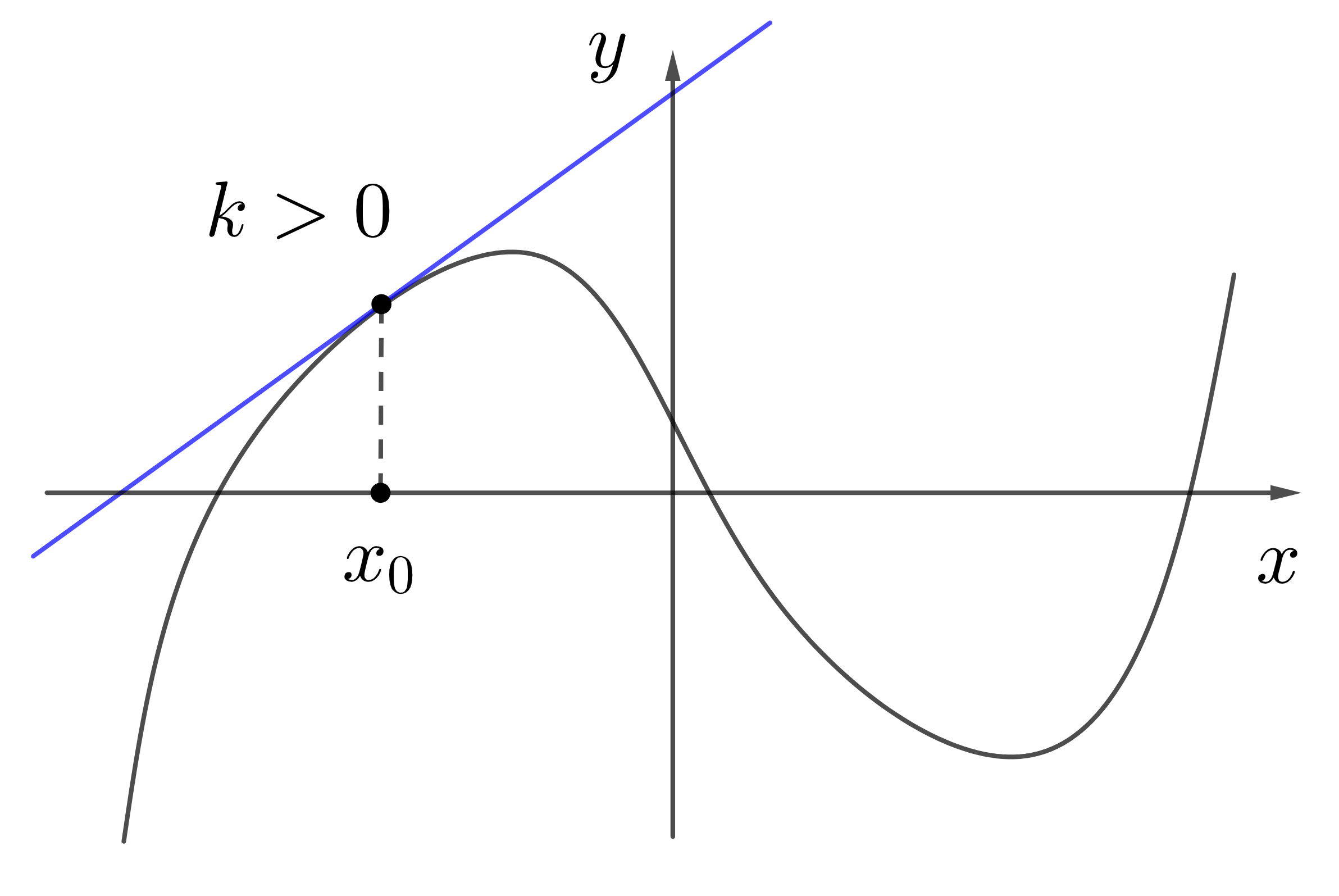
Если касательная возрастает, то \(k>0\) и производная в этой точке будет положительной.
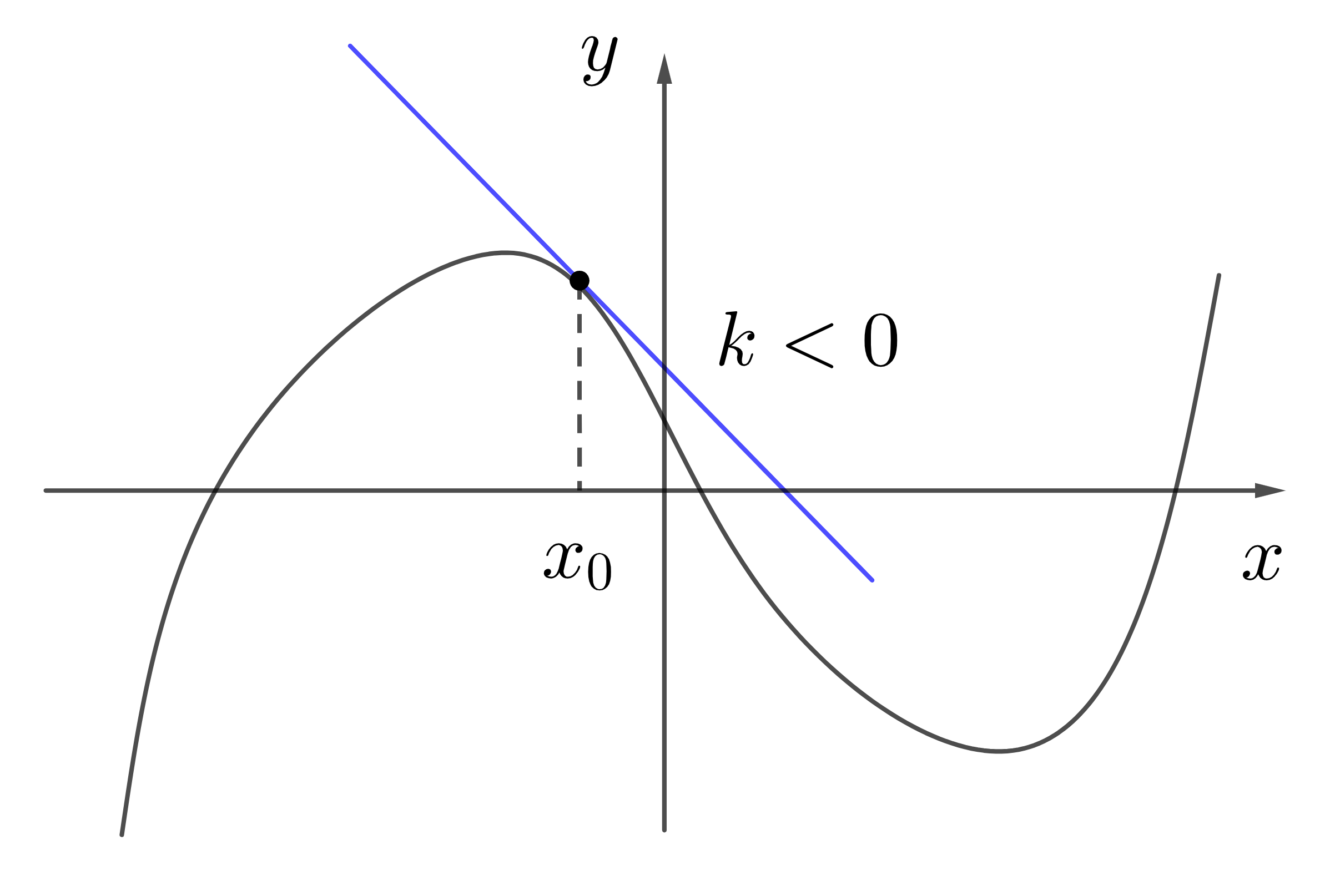
Если касательная убывает, то \(k<0\) и производная в этой точке будет отрицательной.
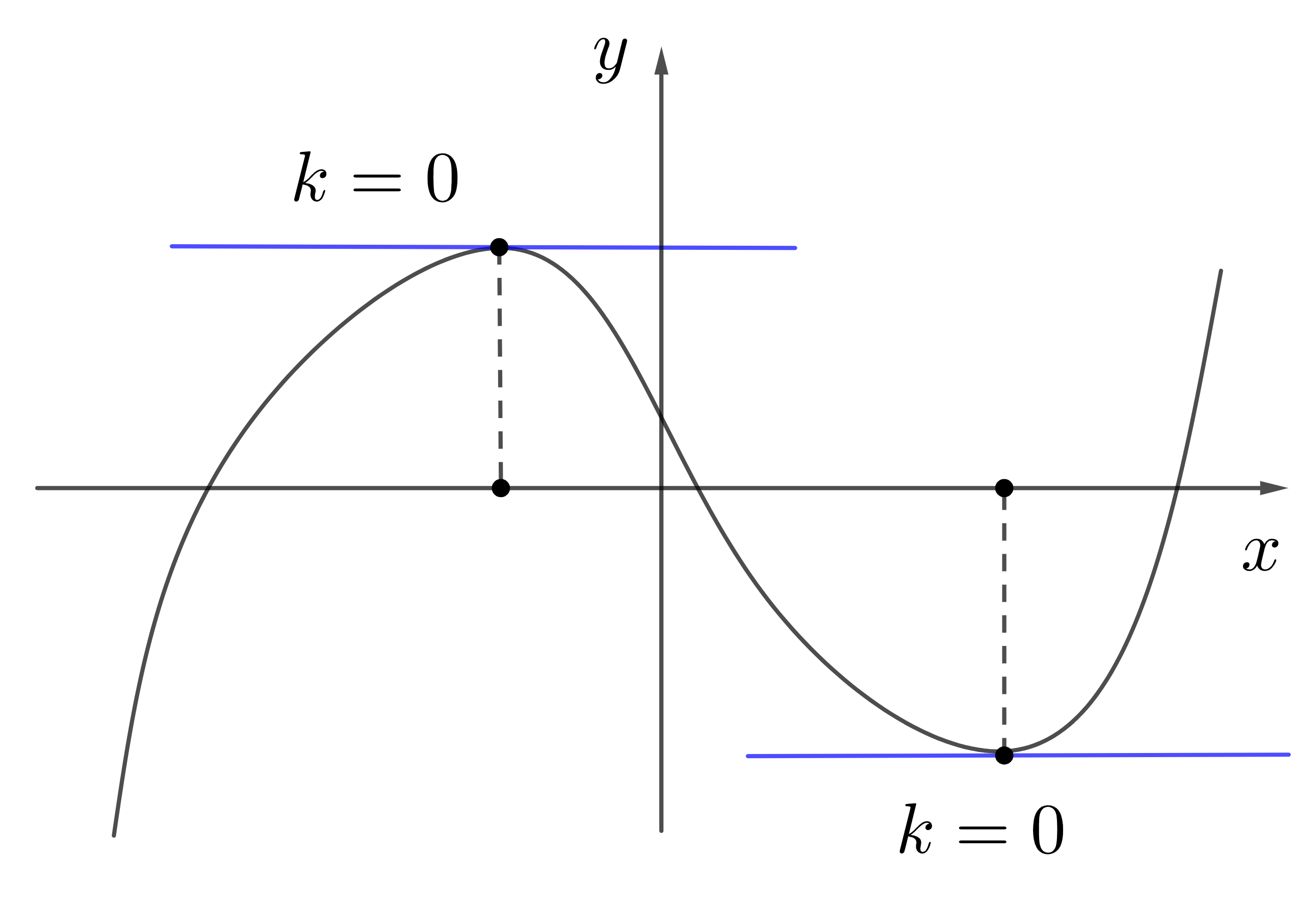
В точках, где функция достигает локальный минимум или максимум, \(f'(x)=k=0\). Эти точки называются экстремумы
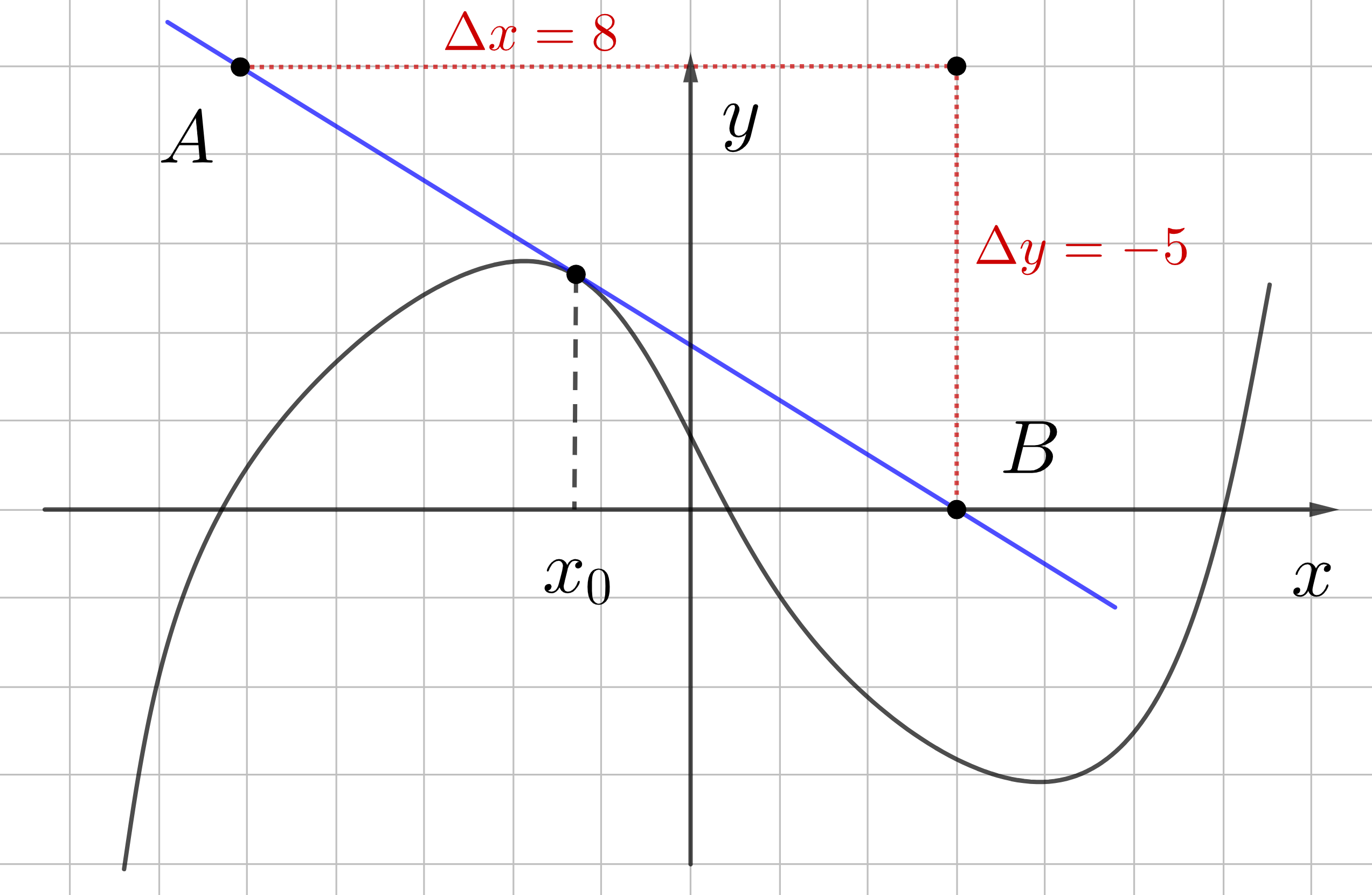
Как искать коэффицент наклона \(k\)
1. Находим две целые точки, через которые проходит касательная. (Точки А и В).
2. Достраиваем рисунок до прямоугольного треугольника.
3. \(k=\dfrac{\Delta y}{\Delta x}=\dfrac{-5}{8}\) - это и есть значение производной в точке \(x_0\)
Записаться на пробный урок ЕГЭ по профильной математике https://marseltutor.ru/
Пример 1. На рисунке изображен график функции \(y=f(x)\). Найдите количество точек, в которых касательная к графику функции параллельна прямой \(y=-5\).
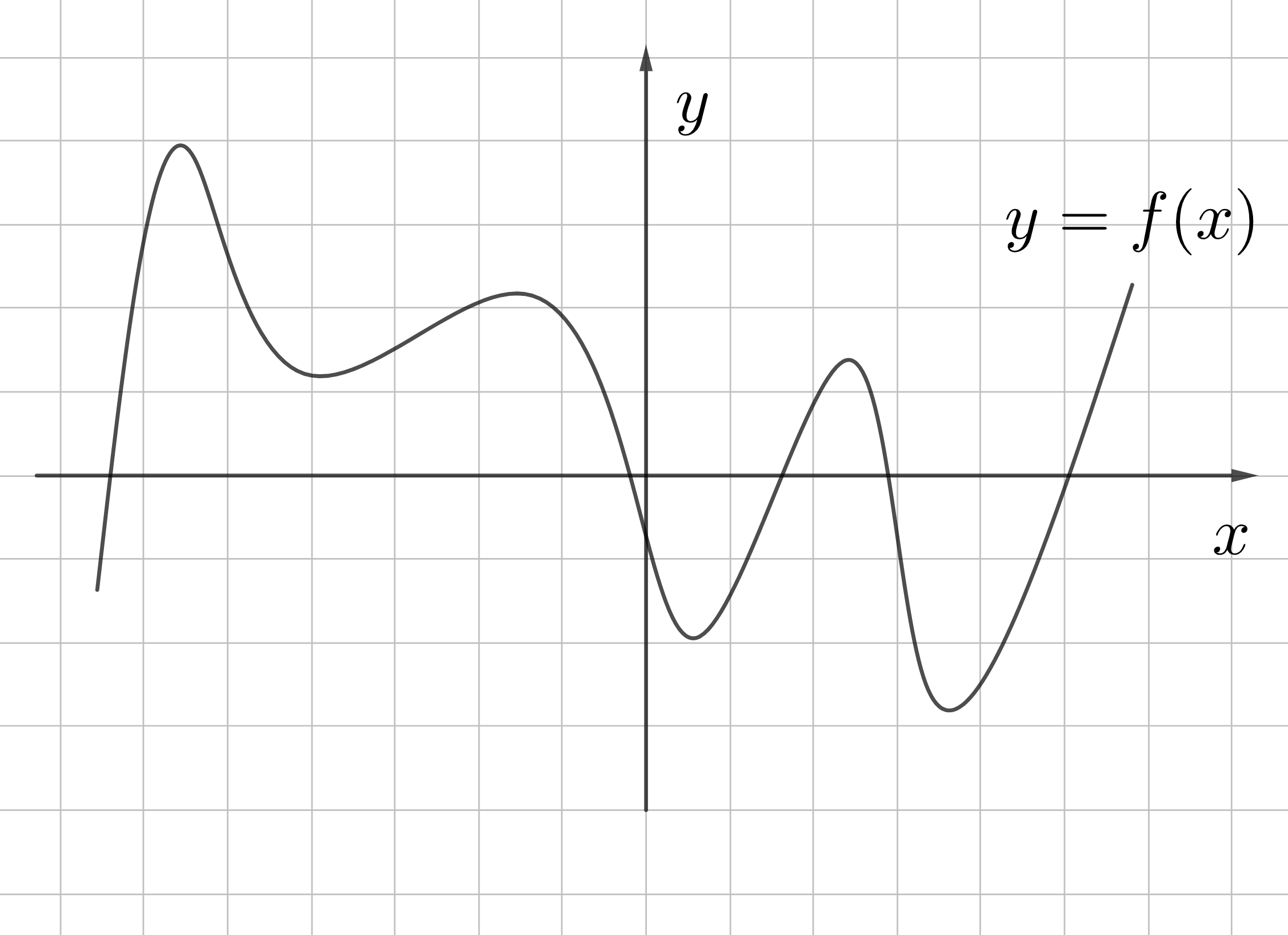
Прямая \(y=-5\) - это горизонтальная прямая, которая пересекает ось \(y\) в точке -5 и проходит параллельно оси \(x\). Значит \(k=0\)
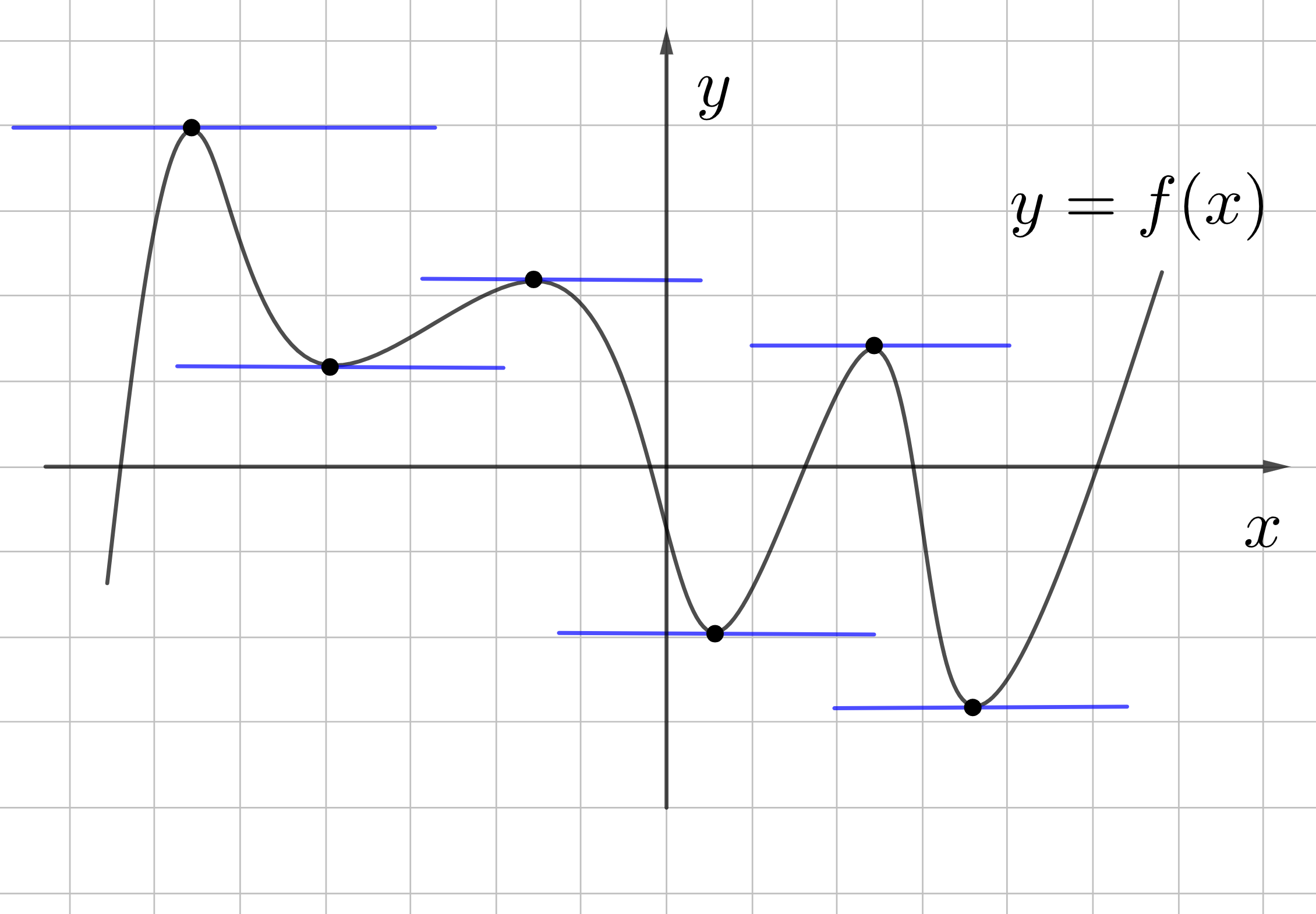
Нам подходят все точки локального минимума и максимума. Таких точек 6
Ответ: 6
Если на рисунке дается не график функции, а график производной, то по нему можно посмотреть при каком значении \(x\) какой будет коэффициент наклона.
Пример 2. На рисунке изображен график производной функции \(f(x)\). Найдите абсциссу точки, в которой касательная к графику функции \(f(x)\) параллельна прямой \(y=2 x-1\) или совпадает с ней.

Решение. Обратите внимание, в отличие от предыдущей задачи, здесь дан график производной \(y=f'(x)\).
Коэффициент наклона прямой \(y=2 x-1\) равен \(k=2\). Находим, при каком значении \(x\) производная будет равна 2.
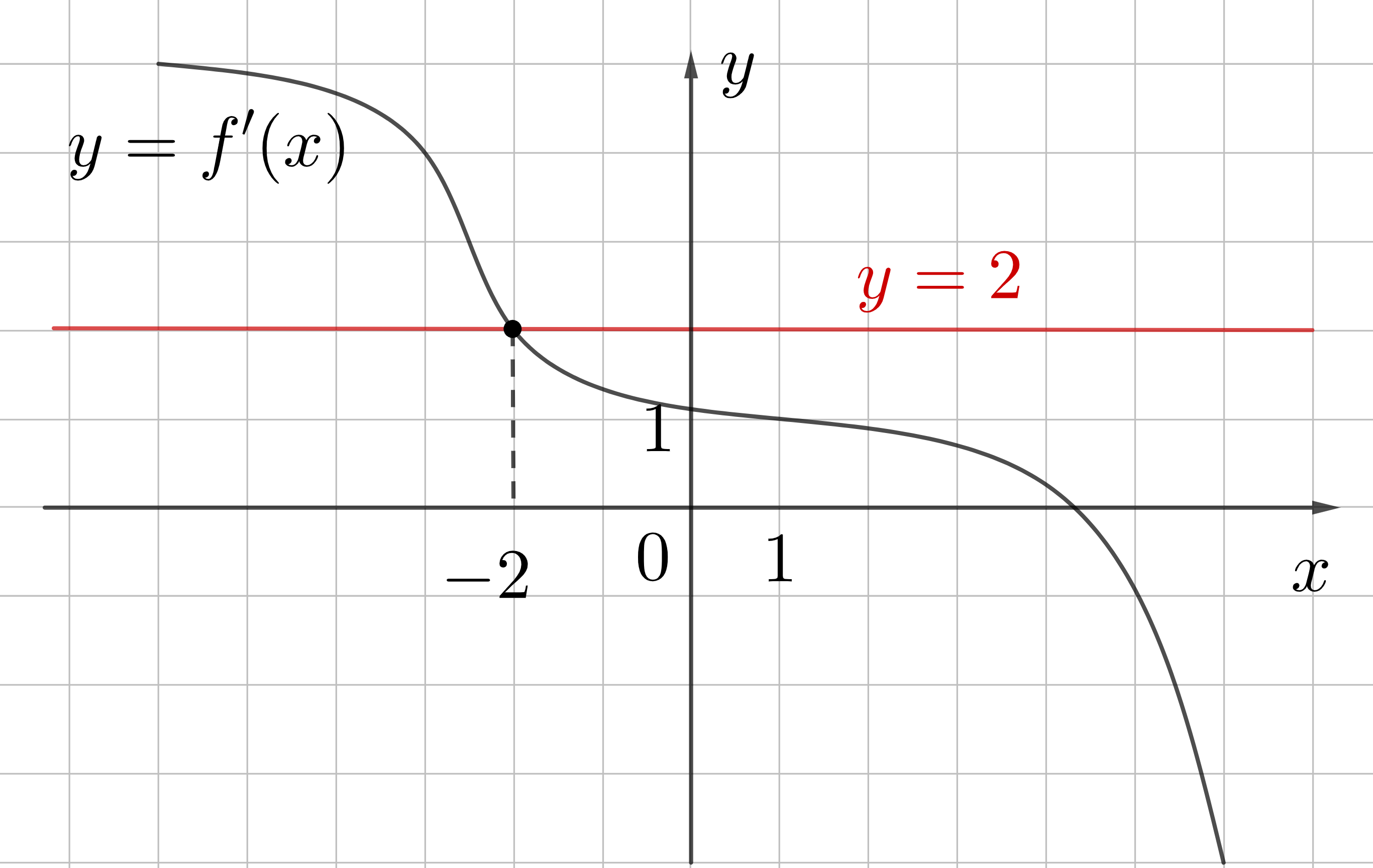
При \(x=-2\) производная равна 2
Ответ: -2
Пример 3. На рисунке изображен график производной функции \(f(x)\). Найдите количество таких чисел \(x\), что касательная к графику функции \(f(x)\) в точке с абсциссой \(x\) параллельна прямой \(y=-2x+7\) или совпадает с ней.
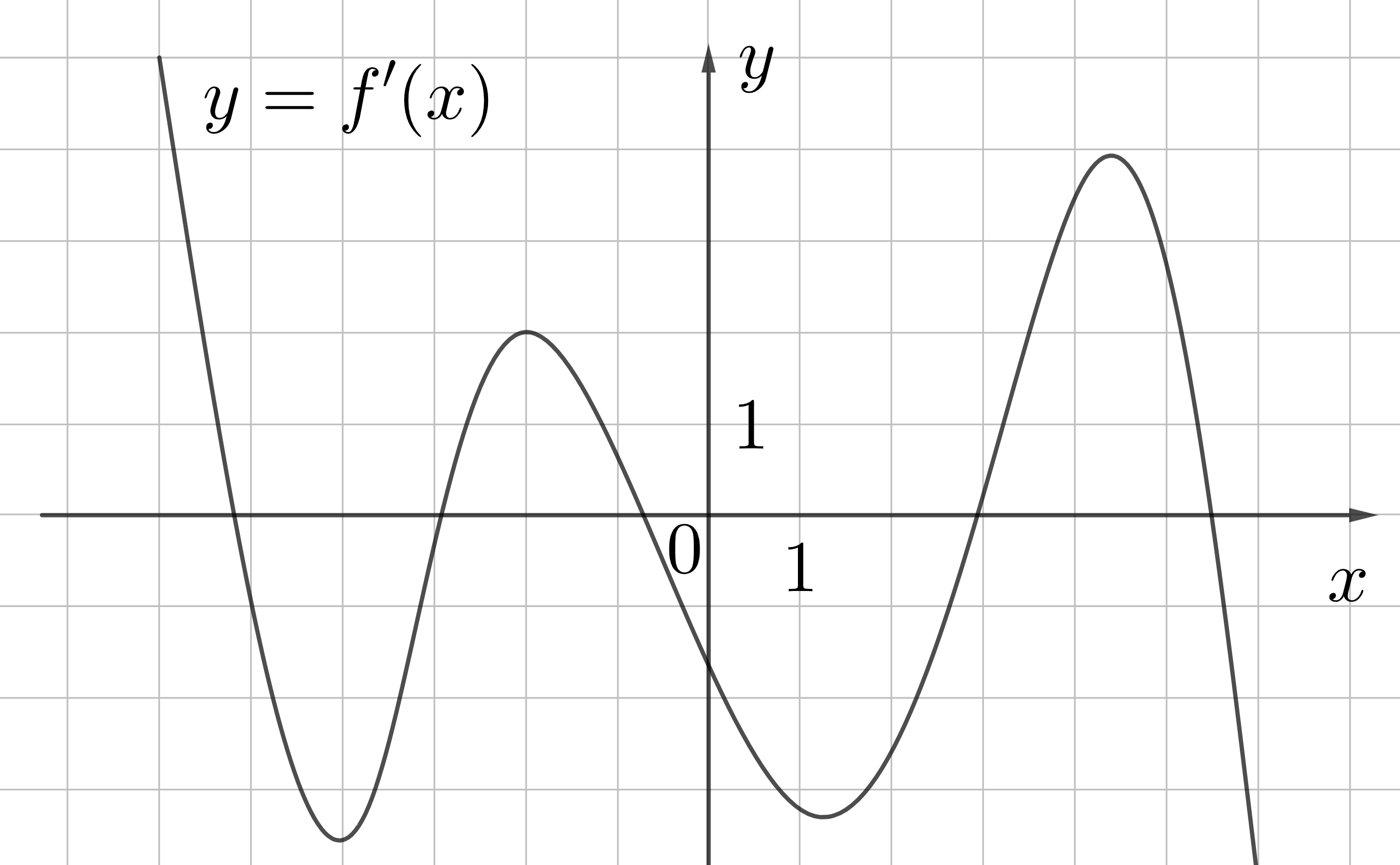
Решение. Дан график производной, а не функции.
Так как прямая \(y=-2x+7\) имеем \(k=-2\), нам нужно по графику найти точки, в которых производная будет равна -2.
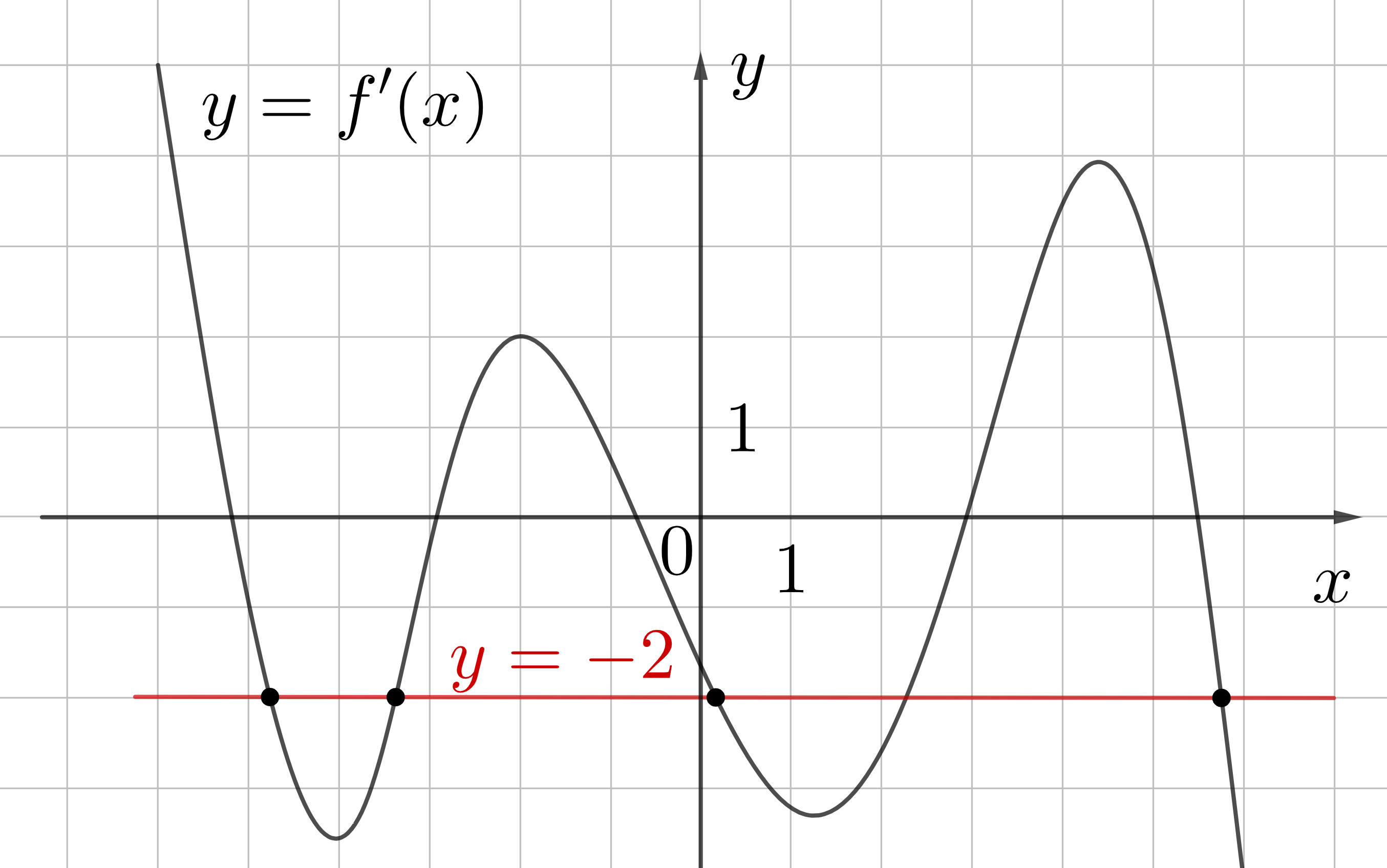
Для удобства прочертим прямую и увидим все точки. Их всего 4.
Ответ: 4
Как по графику функции оценить значение производной.
Там где функция убывает (точки \(A, B, C, E, K, L\), производная отрицательная. Функция везде убывает с разной скоростью. Например, в точке \(A\) - резкое падение, в точке \(B\) - плавнее, а в точке \(C\) падение практически остановилось. Поэтому производная в точке \(A\) будет больше по модулю, чем в точке \(B\), в точке \(C\) близка к 0. В точке \(A\) - значение производной будет наименьшим на всем промежутке.
Там где функция возрастает (точки \(D, G\)) - производная положительная. В точке \(D\) график растет быстрее, поэтому значение производной в точке \(D\) больше, чем в \(G\)
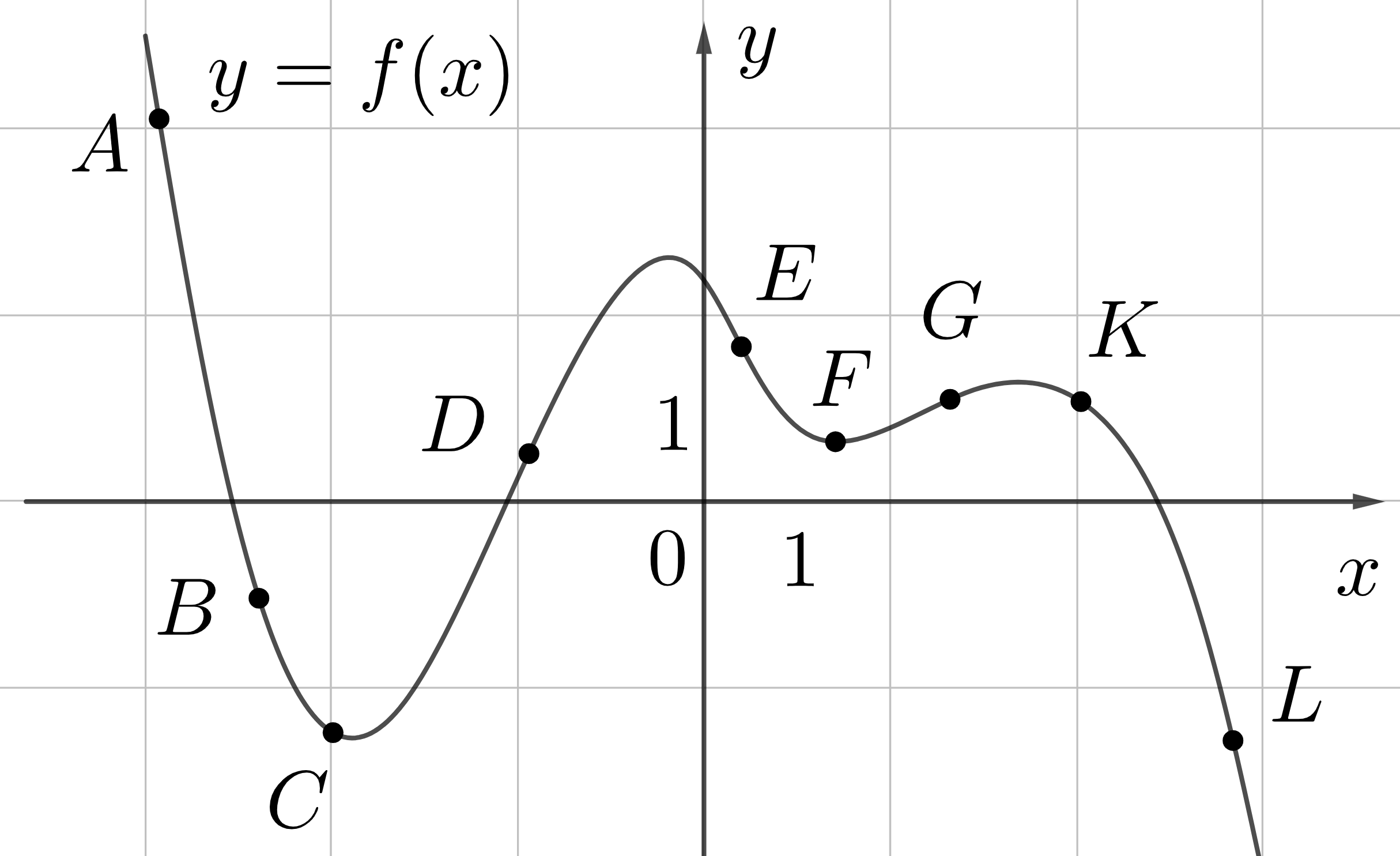
Для наглядности привожу схему
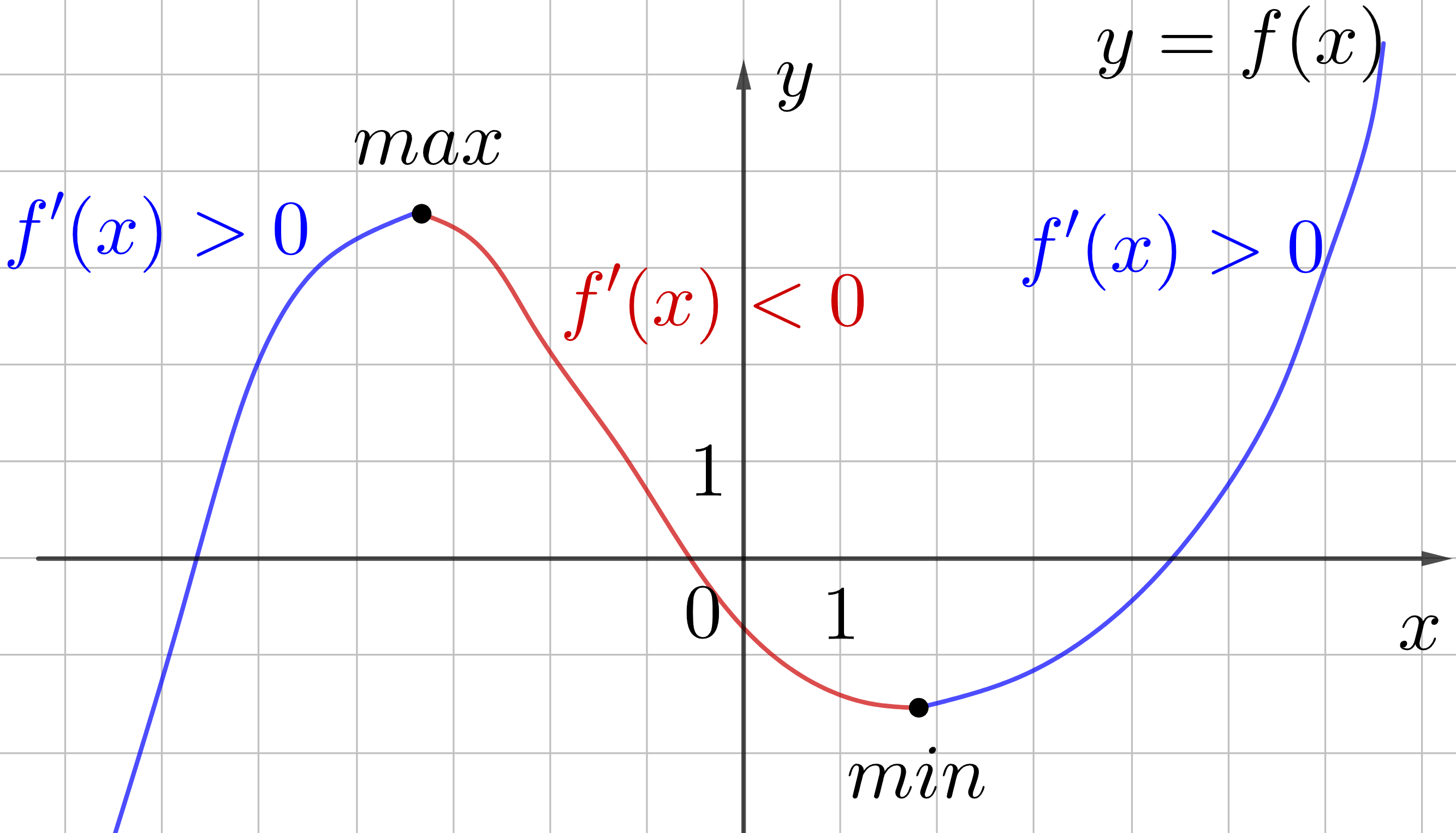
По графику производной просто понять, где будет точка максимума и минимума (экстремумы)

Автор: Нуртдинов Марсель - преподаватель по математике
