1 задание ЕГЭ профильная математика. Все формулы
Теория 1 задание ЕГЭ профиль
1. Сумма смежных углов равна \(180^o\)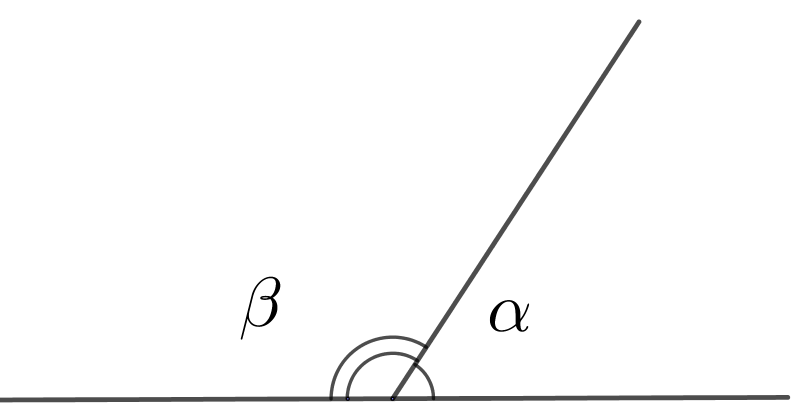
2. Вертикальные углы равны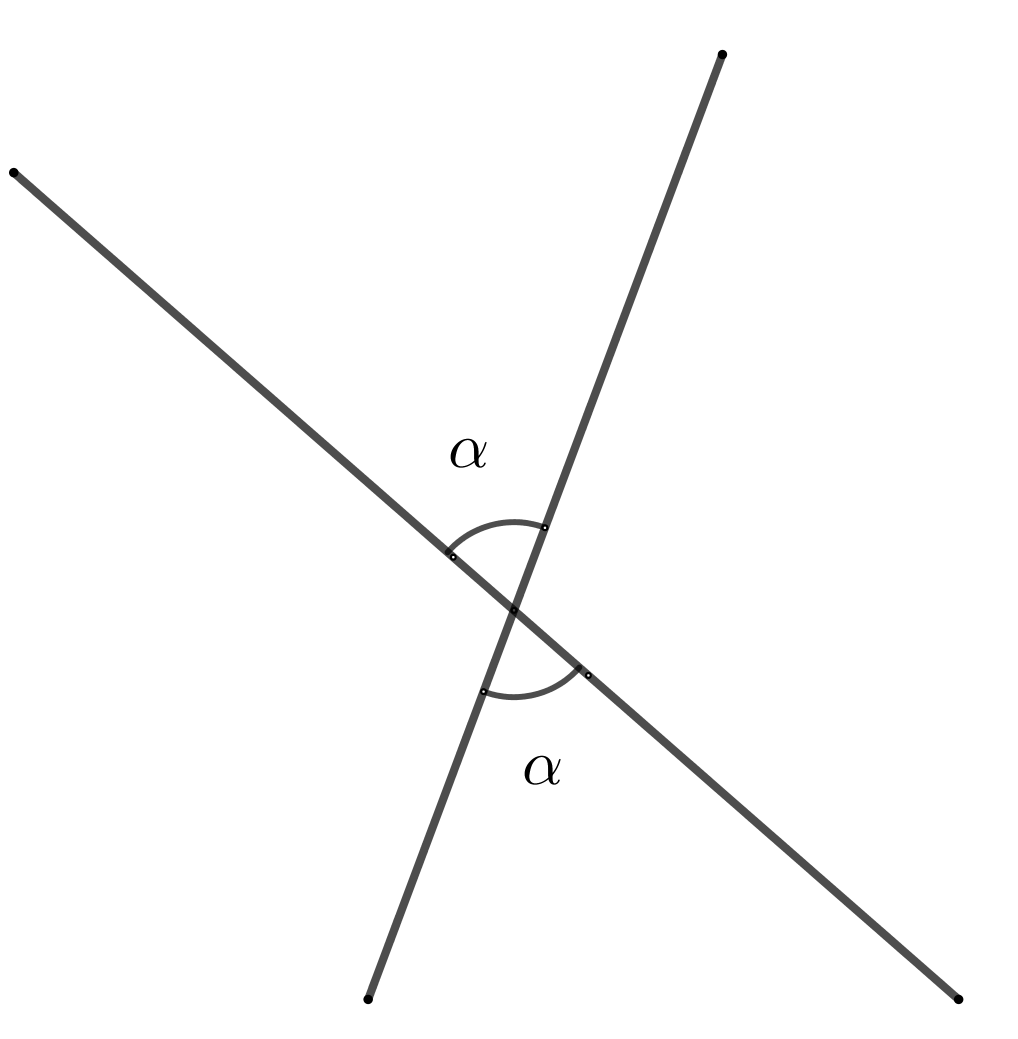
3. Накрест лежащие углы равны (если прямые параллельны)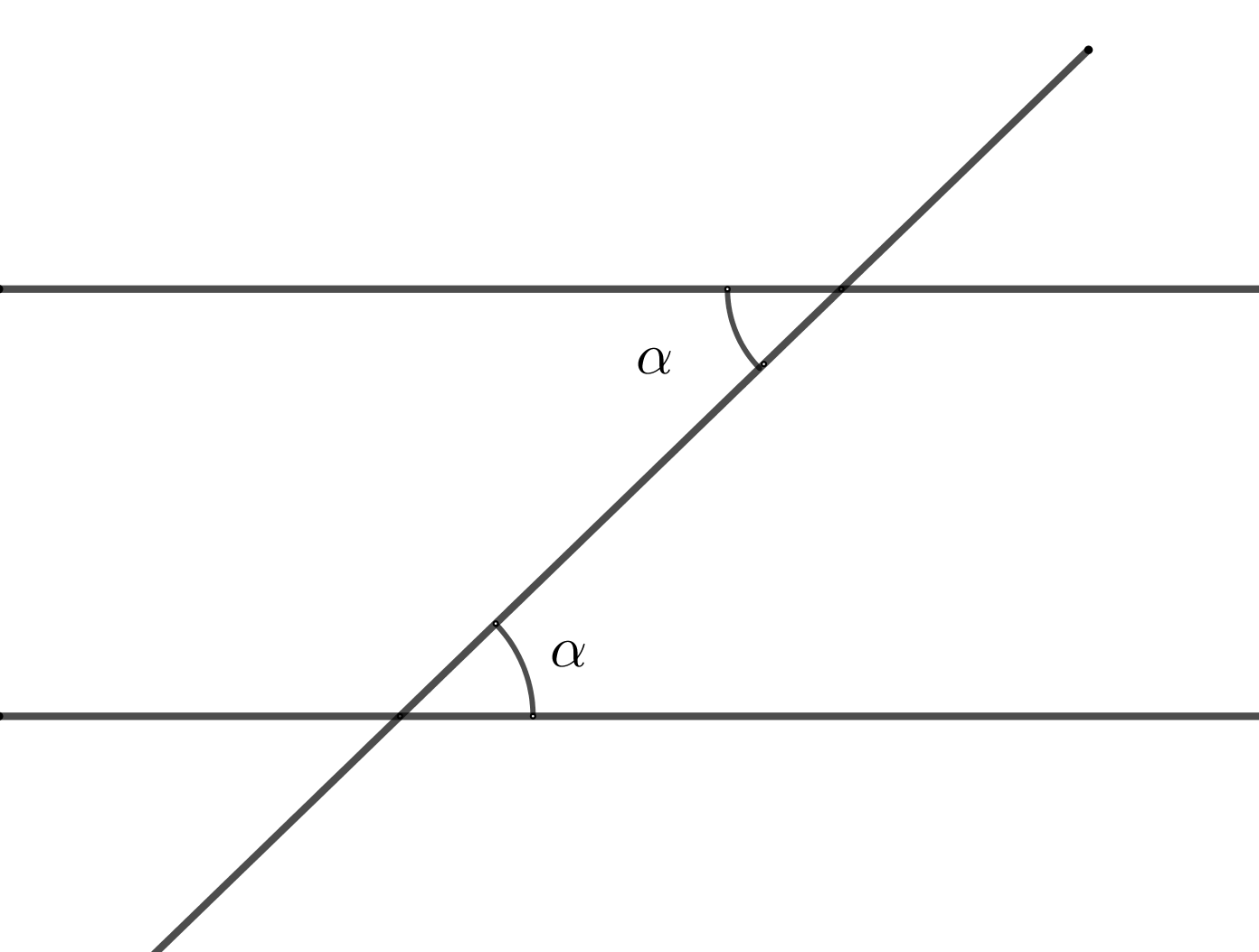 
4. Соответственные углы равны (если прямые параллельны)
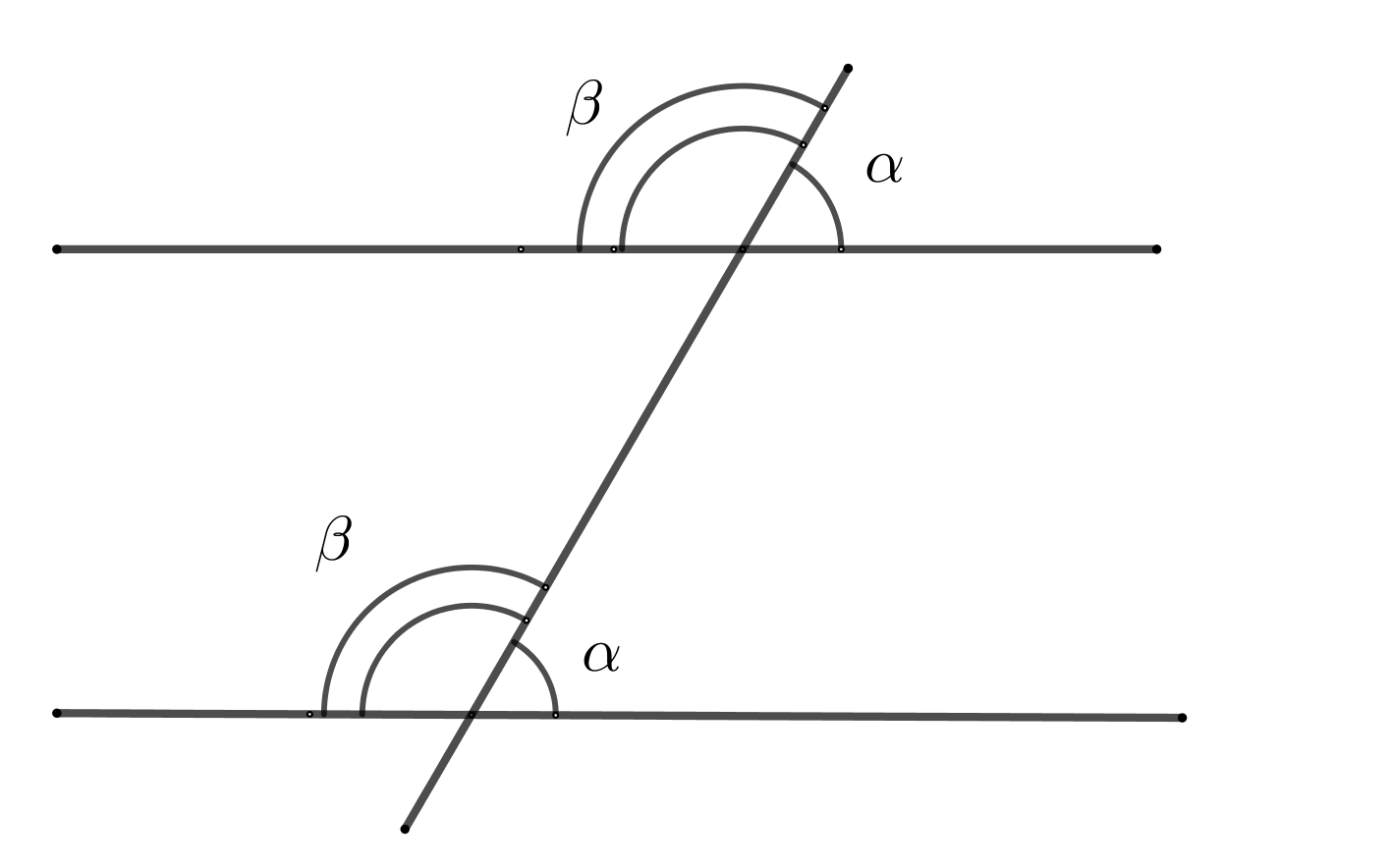
5. Сумма односторонних углов равна \(180^o \) (если прямые параллельны)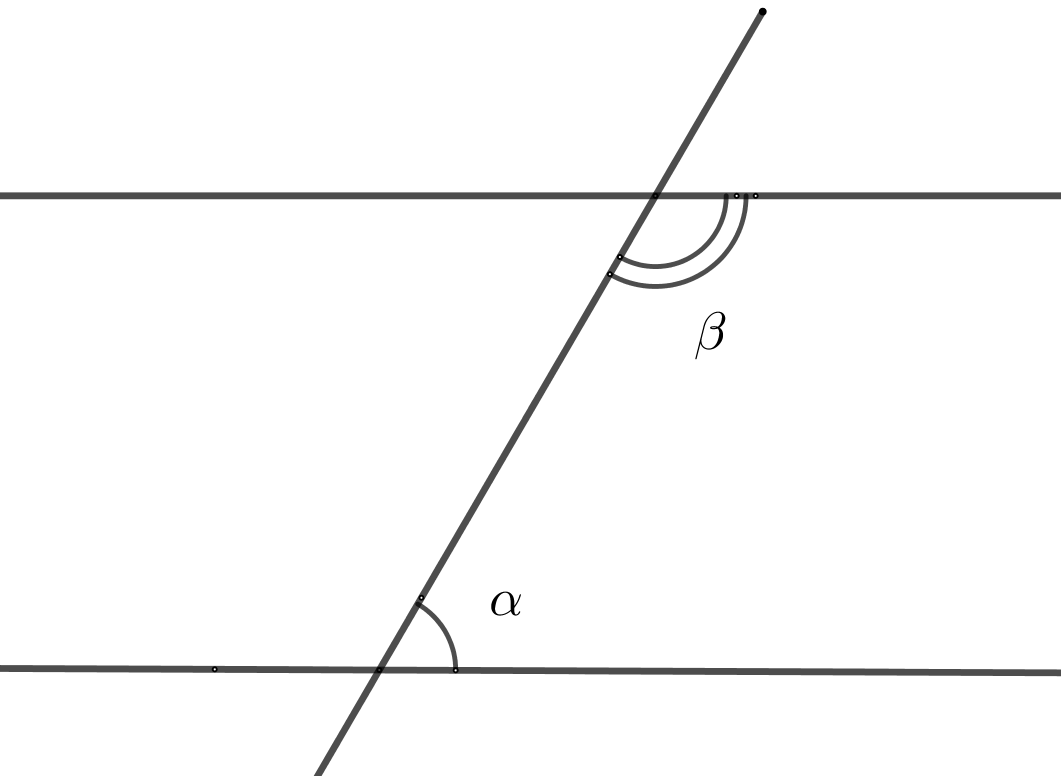
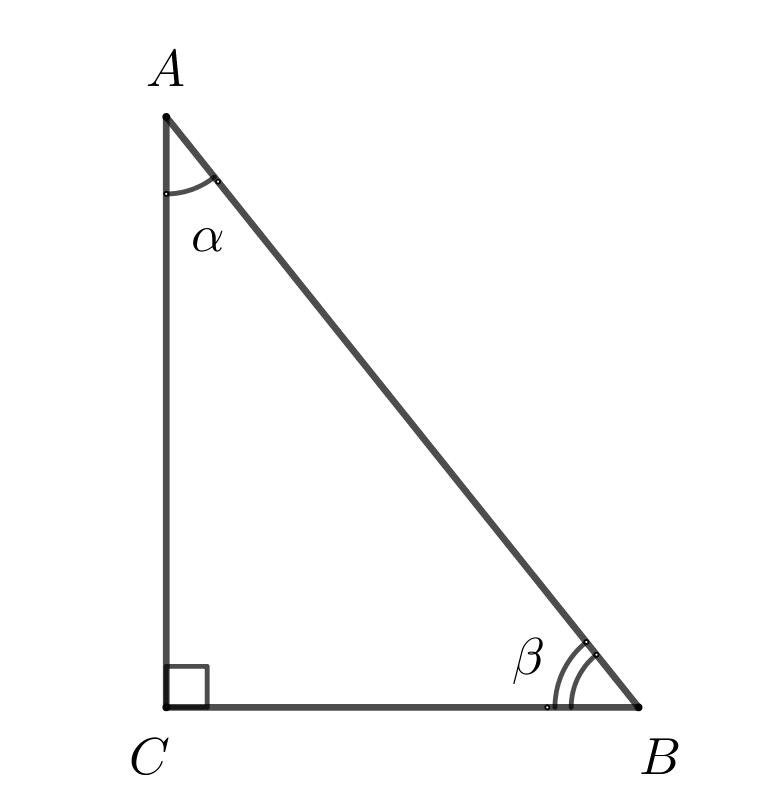
6. Синус, косинус, тангенс
\(\sin \alpha = \dfrac{BC}{AB}\) - отношение противолежащего катета на гипотенузу.
\(\cos\alpha=\dfrac{AC}{AB}\) - отношение прилежащего катета на гипотенузу.
\(tg \alpha =\dfrac{BC}{AC}\) - отношение противолежащего катета на прилежащий.
\(\sin^2\alpha+\cos^2\beta=1\)
\(\sin\alpha =\cos\beta\)
\(\cos\alpha=\sin\beta\)
\(tg\alpha=ctg\beta\)
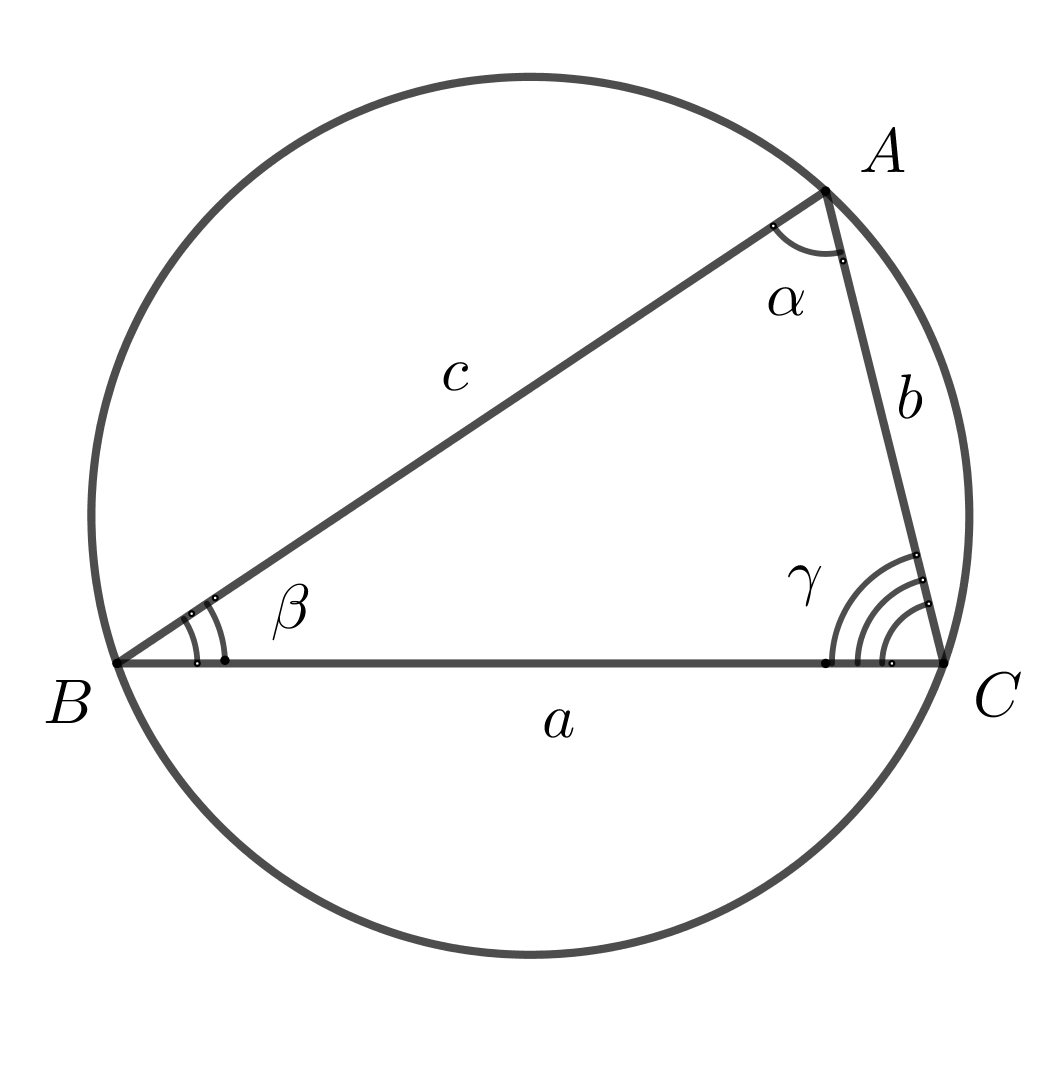
7. Теорема синусов
\(\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}=2R\), где \(R\) - радиус описанной окружности.
Стратегия подготовки к ЕГЭ по профильной математике https://marseltutor.ru/
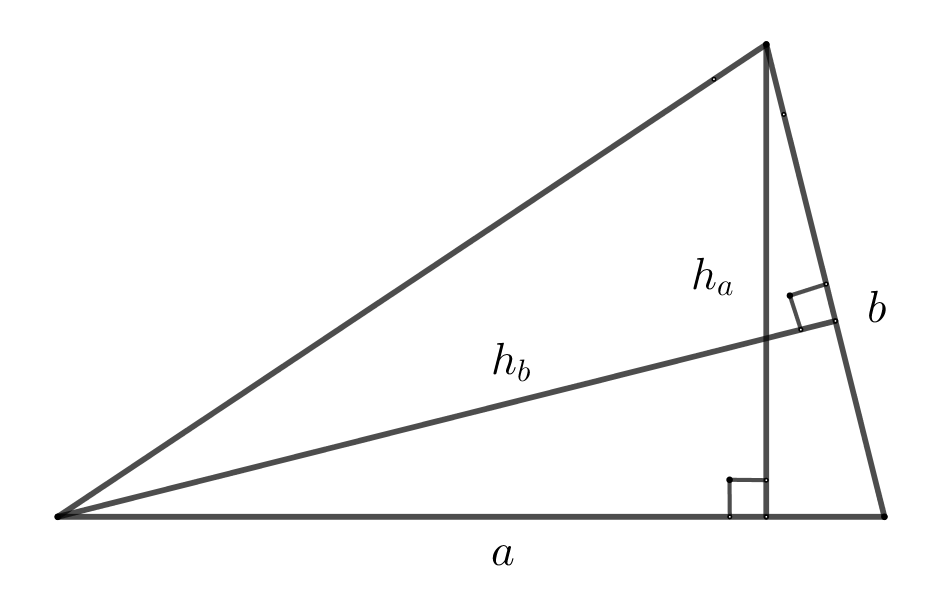
8. Площадь треугольника через высоту и сторону.
\(S=\dfrac{h_a\cdot a}{2}=\dfrac{h_b\cdot b}{2}\)
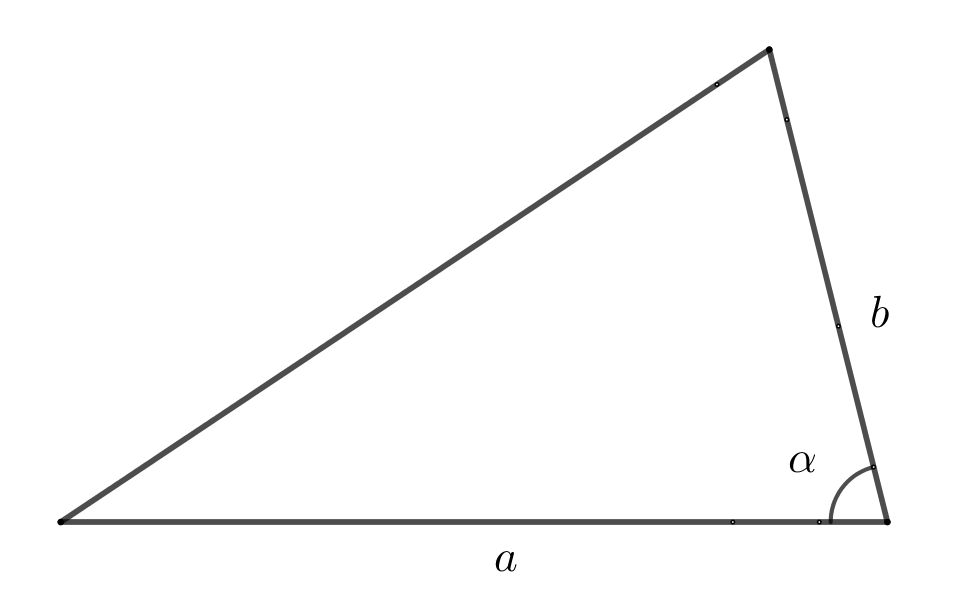
9. Площадь треугольника через две стороны и угол между ними
\(S=\dfrac{a\cdot b\cdot \sin\alpha }{2}\)
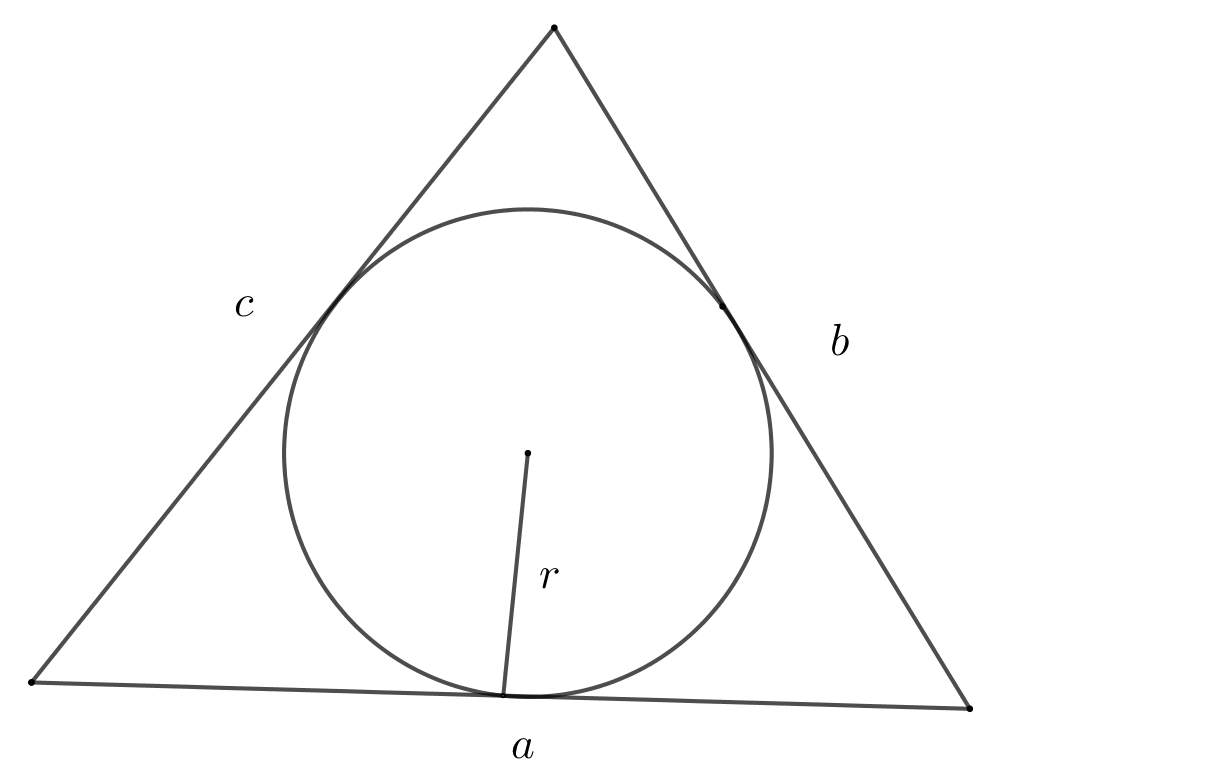
10. Площадь треугольника через радиус вписанной окружности
\(S=pr\), где \(p=\dfrac{a+b+c}{2}\), \(r -\) радиус вписанной окружности.
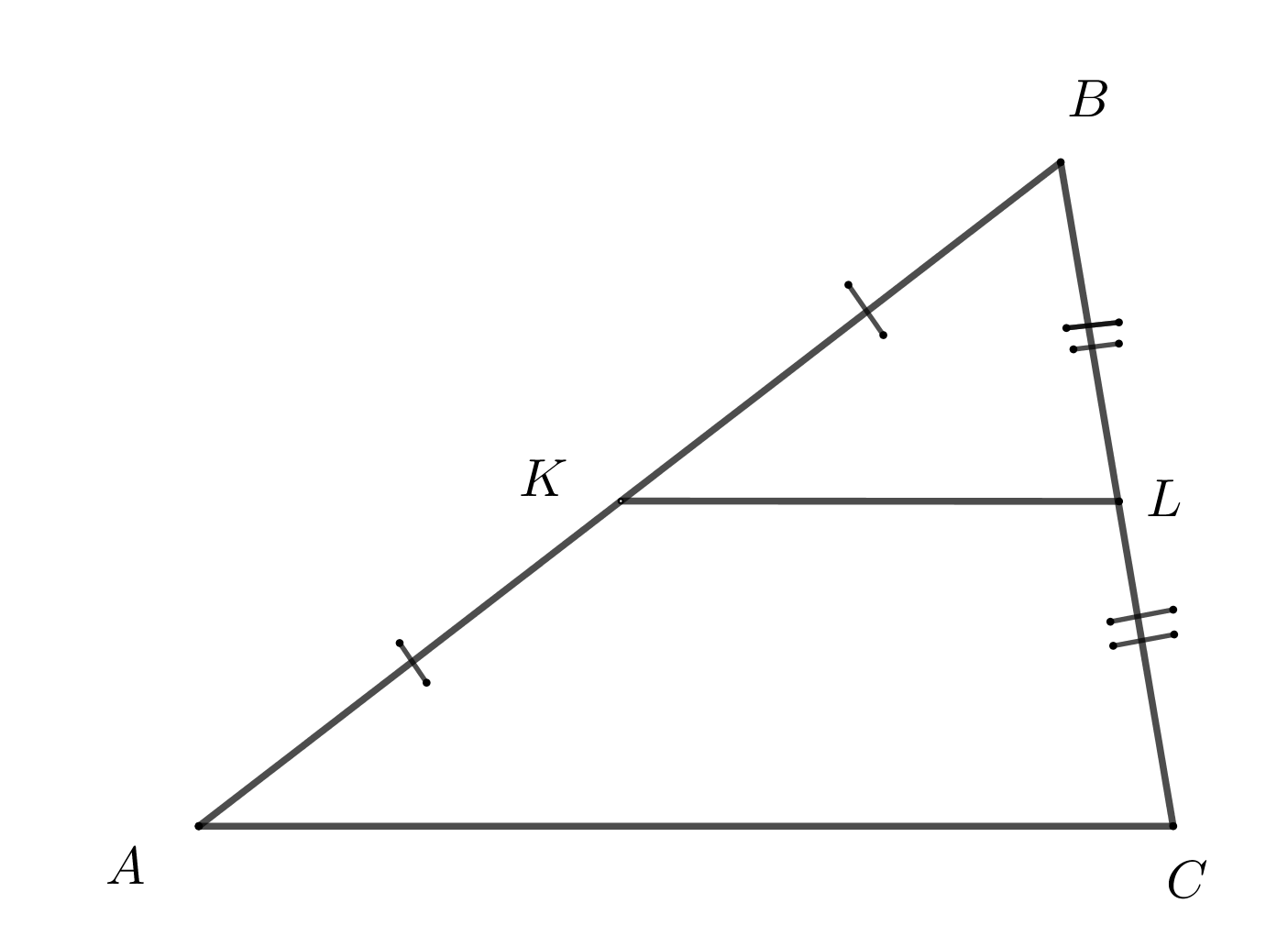
11. Средняя линия - отрезок, соединяющий середины сторон треугольника.
Параллельна боковой стороне и равна ее половине.
\(KL=\dfrac{AC}{2}\)
Средняя линия отсекает треугольник, площадь которого в 4 раза меньше площади основного.
\(S_{KBL}=\dfrac{S_{ABC}}{4}\)
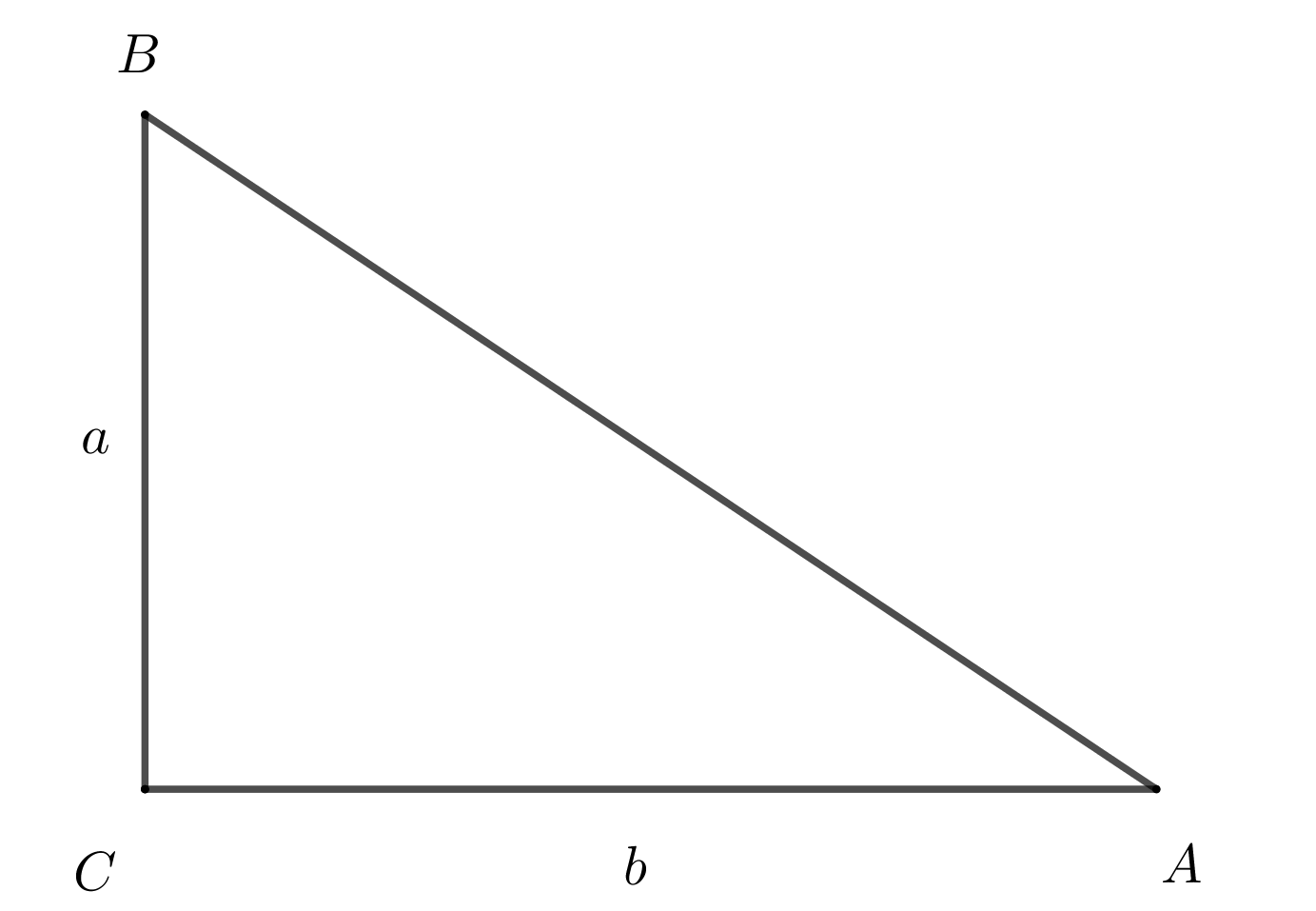
12. Площадь прямоугольного треугольника
\(S=\dfrac{a\cdot b}{2}\)
13. Теорема Пифагора.
\(c^2=a^2+b^2\)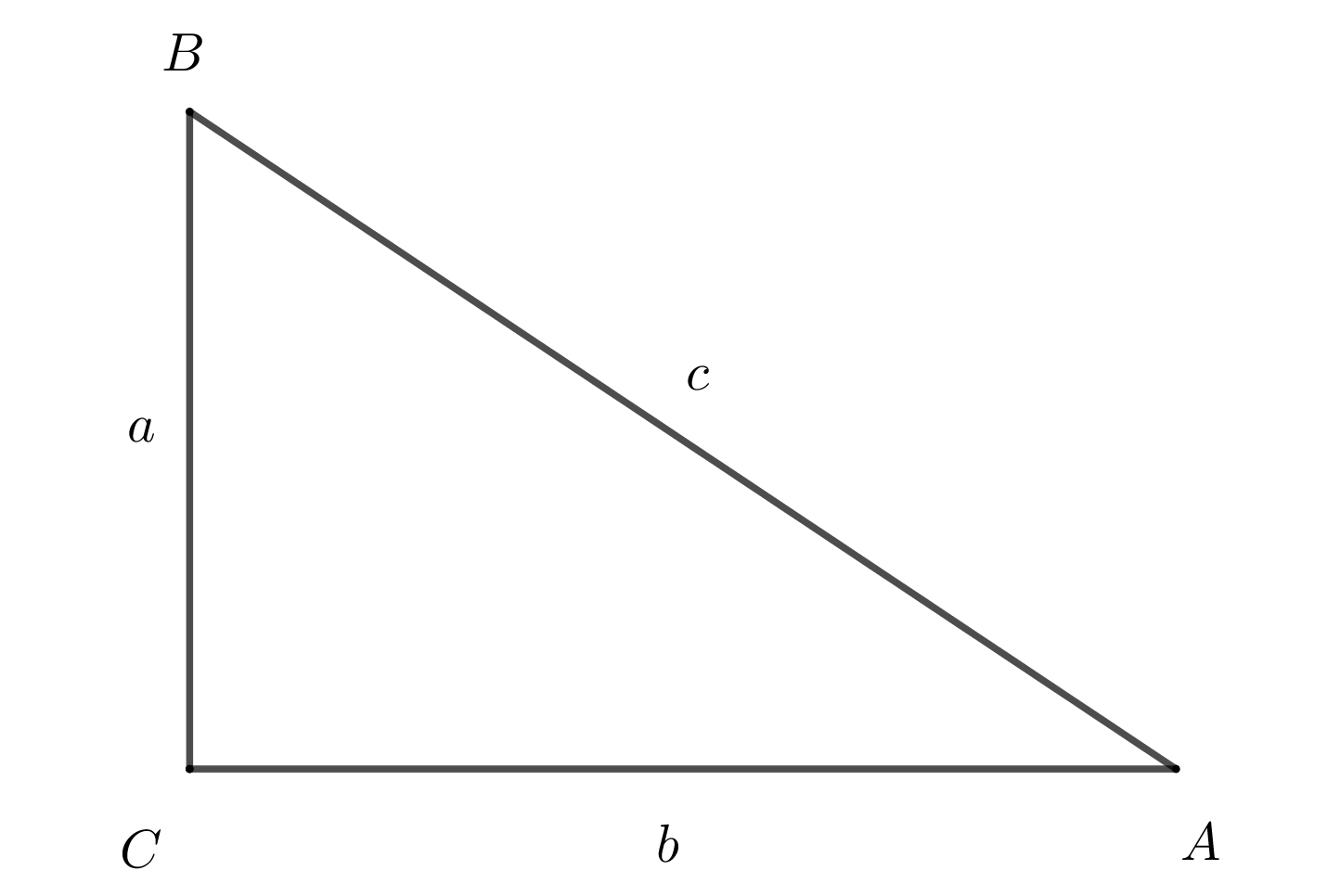
14. Катет, лежащий против угла \(30^o\) равен половине гипотенузы.
Если катет равен половине гипотенузы, то угол против данного катета равен \(30^o\)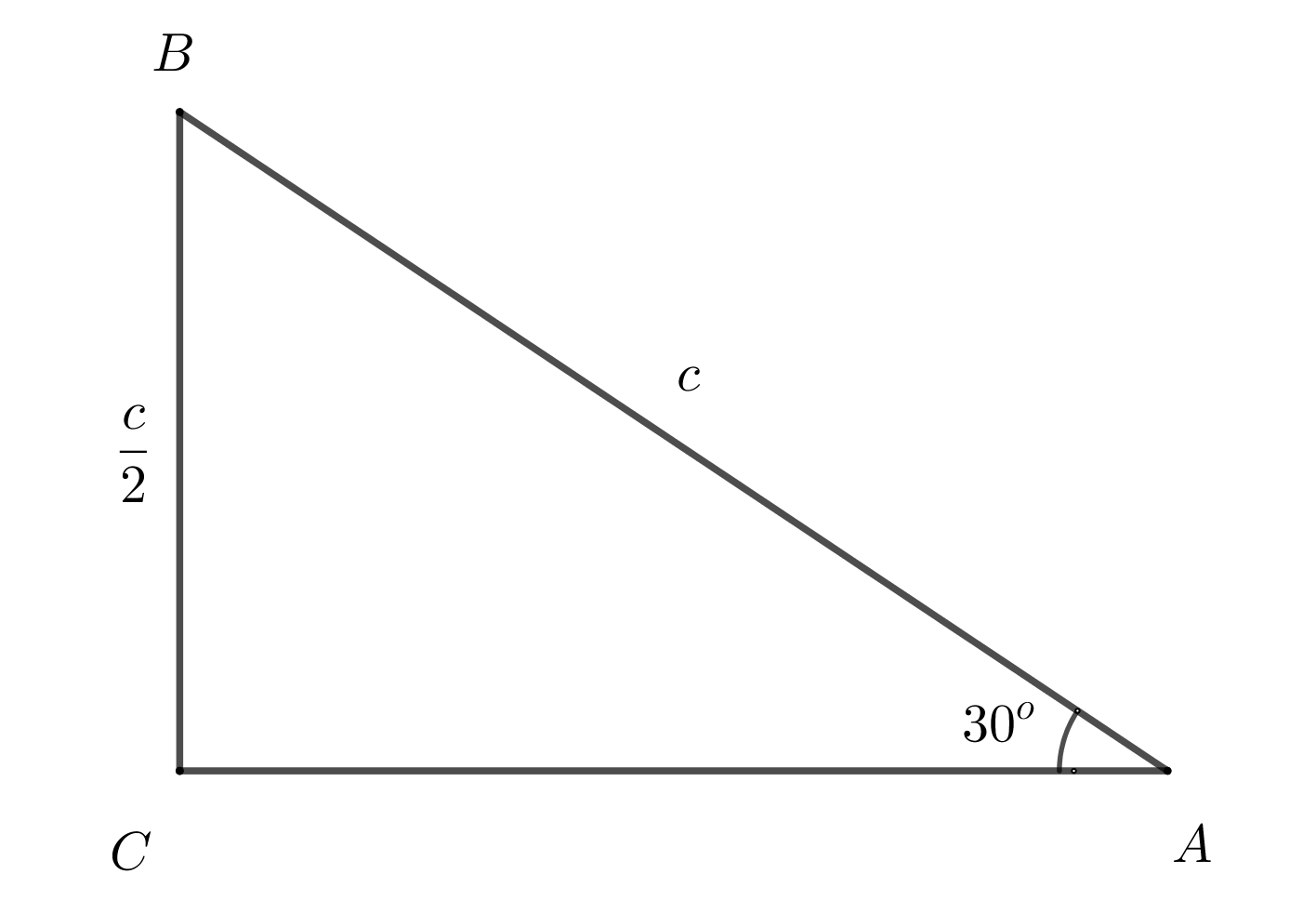
15. Радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы. Центр окружности лежит на середине гипотенузы.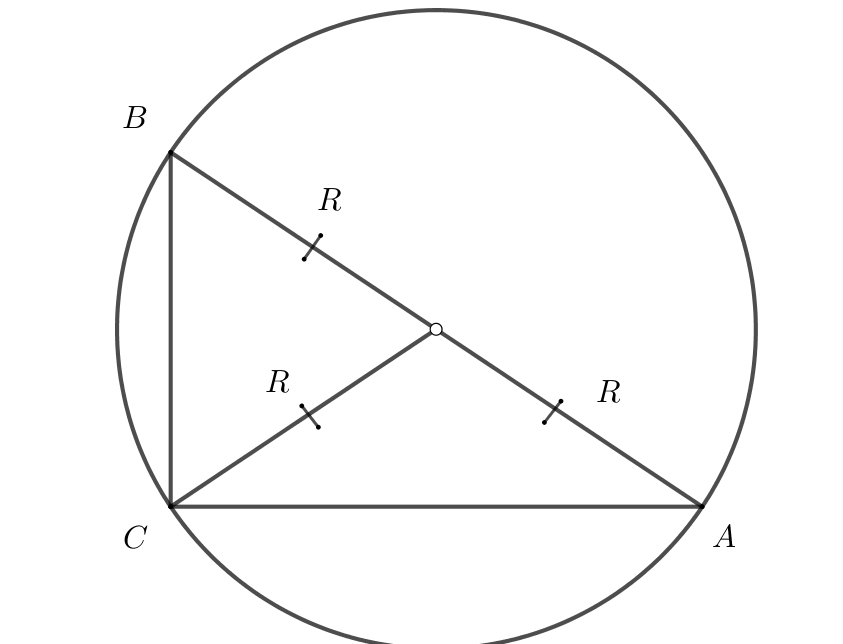 
16. Медиана в прямоугольном треугольнике, проведенная к гипотенузе равна половине гипотенузы. Образуются два равнобедренных треугольника.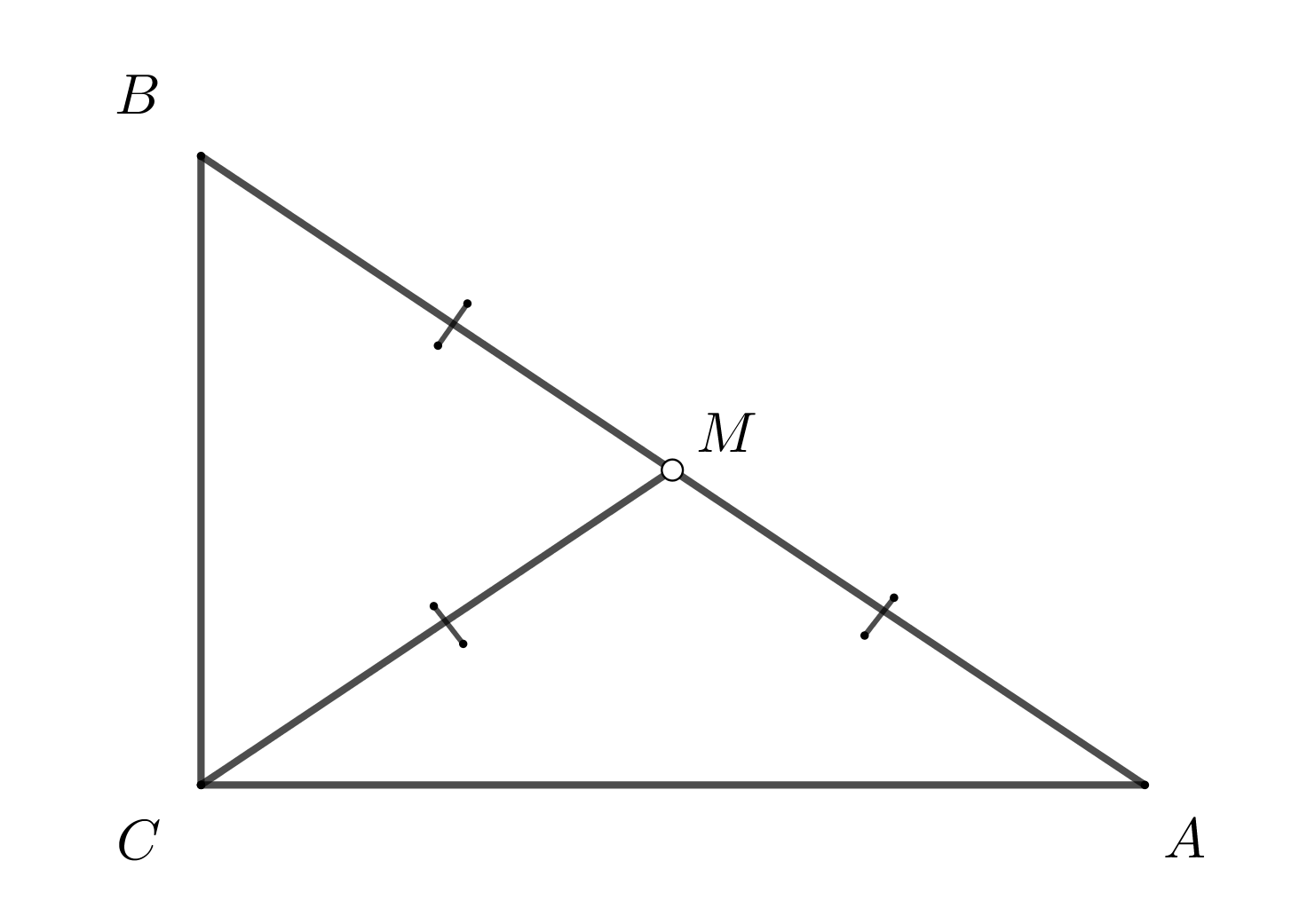
17. В равнобедренном треугольнике углы при основании равны. Высота, проведенная к основанию является медианой и биссектрисой.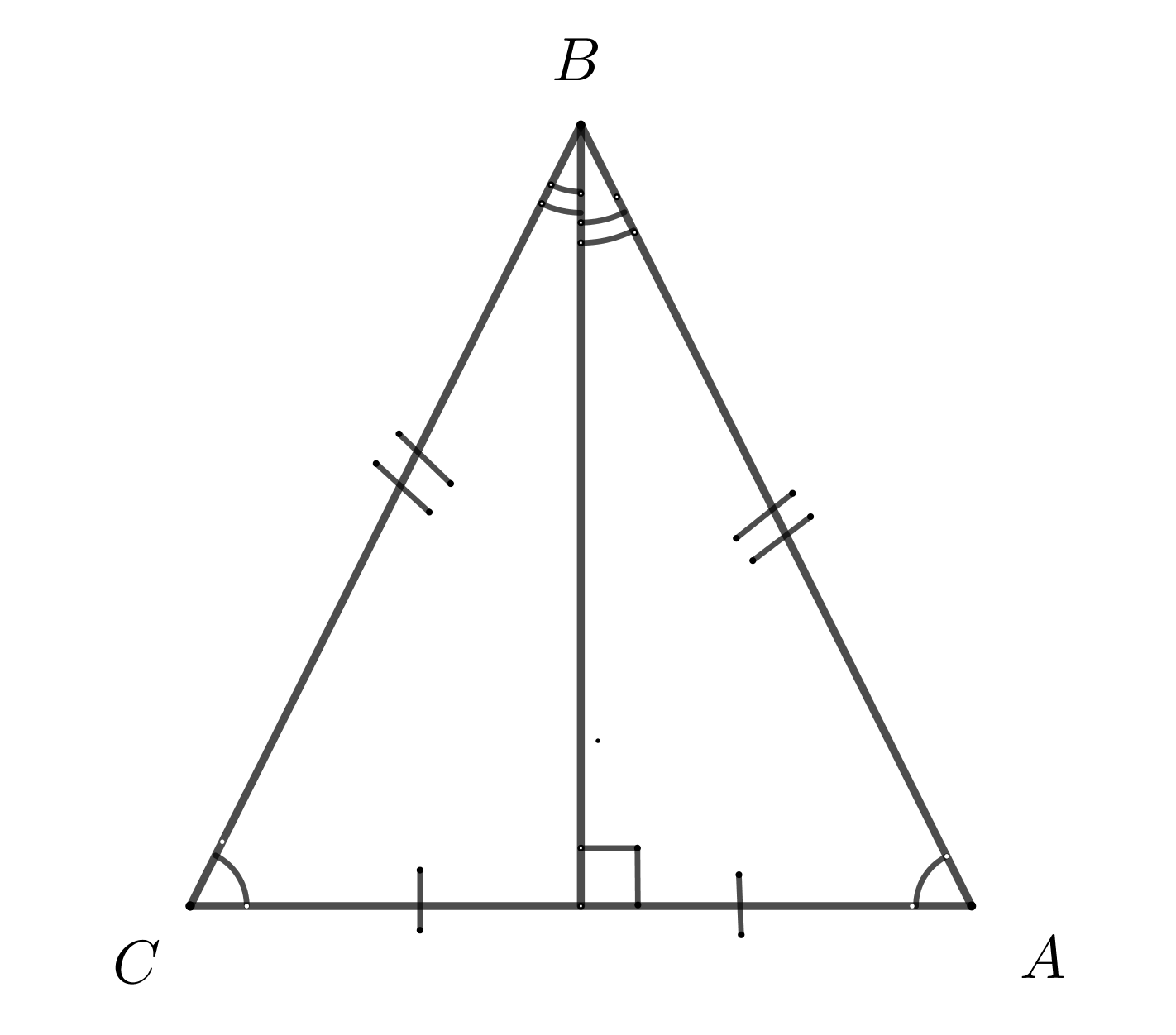 
18. В равностороннем треугольнике все углы равны \(60^o\)
- В равностороннем треугольнике высоты, медианы и биссектрисы совпадают.
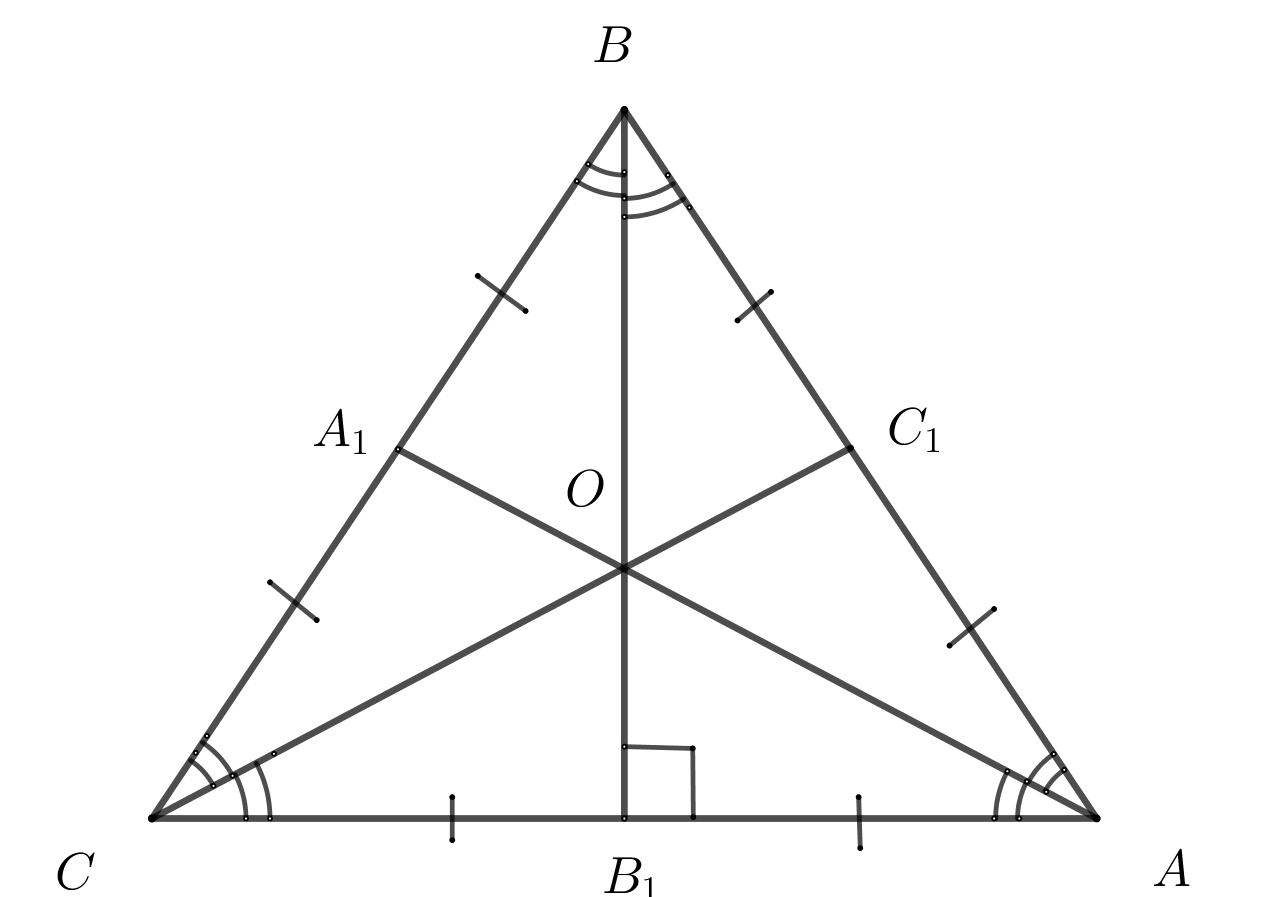
- Центр вписанной и описанной окружности лежат в одной точке.
- Радиус вписанной окружности равен \(\dfrac{1}{3}\) высоты (медианы, биссектрисы)
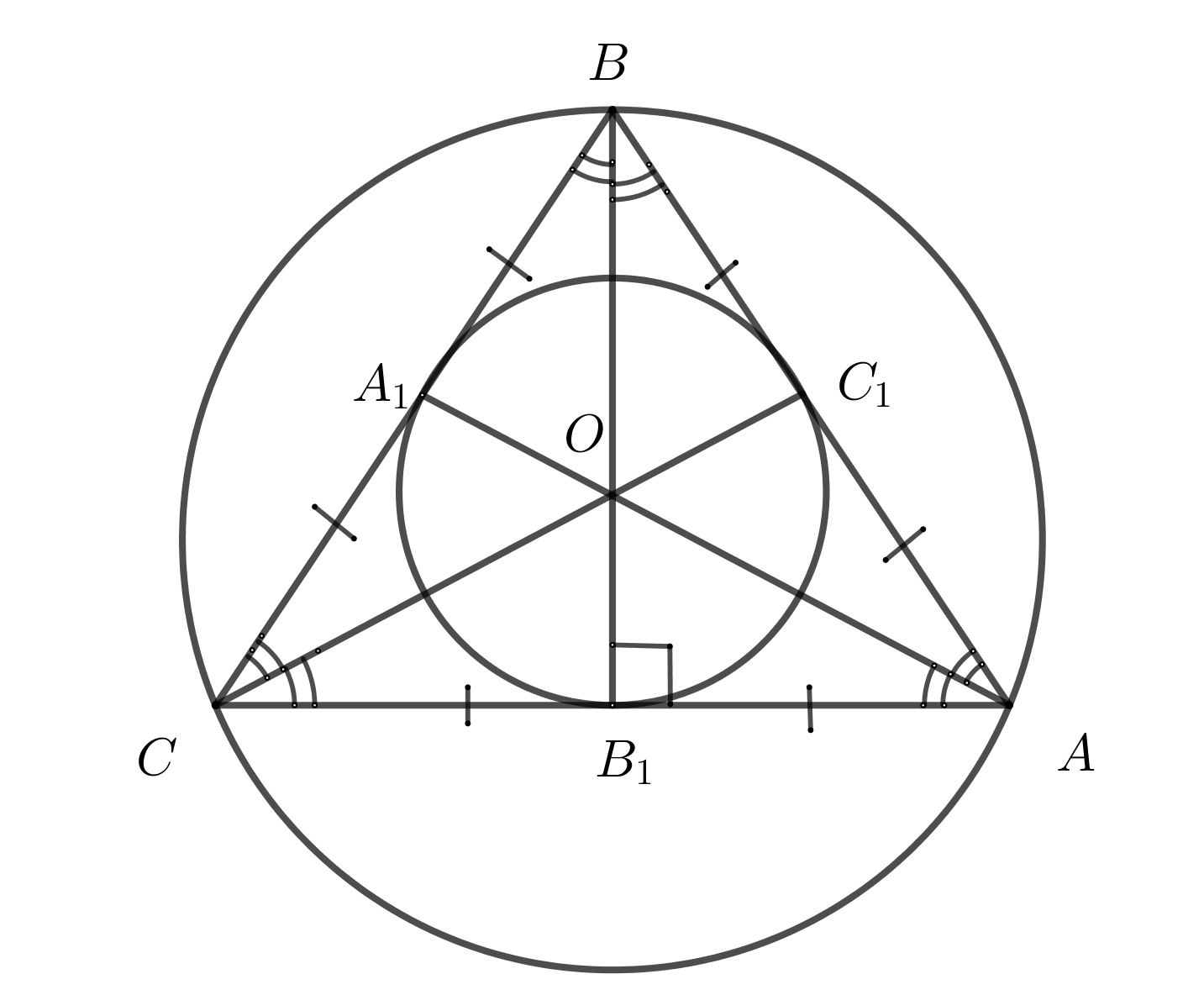
19. Признаки равенства треугольников.
1 признак. По двум сторонам и углу между ними.
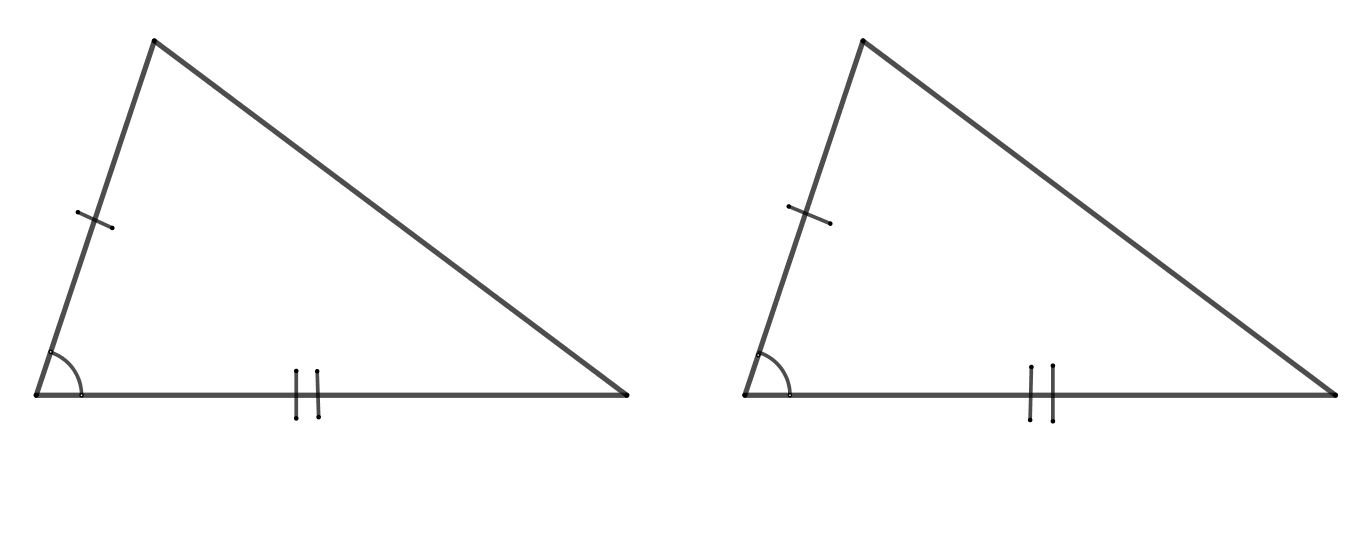
2 признак. По стороне и двум прилежащим углам.
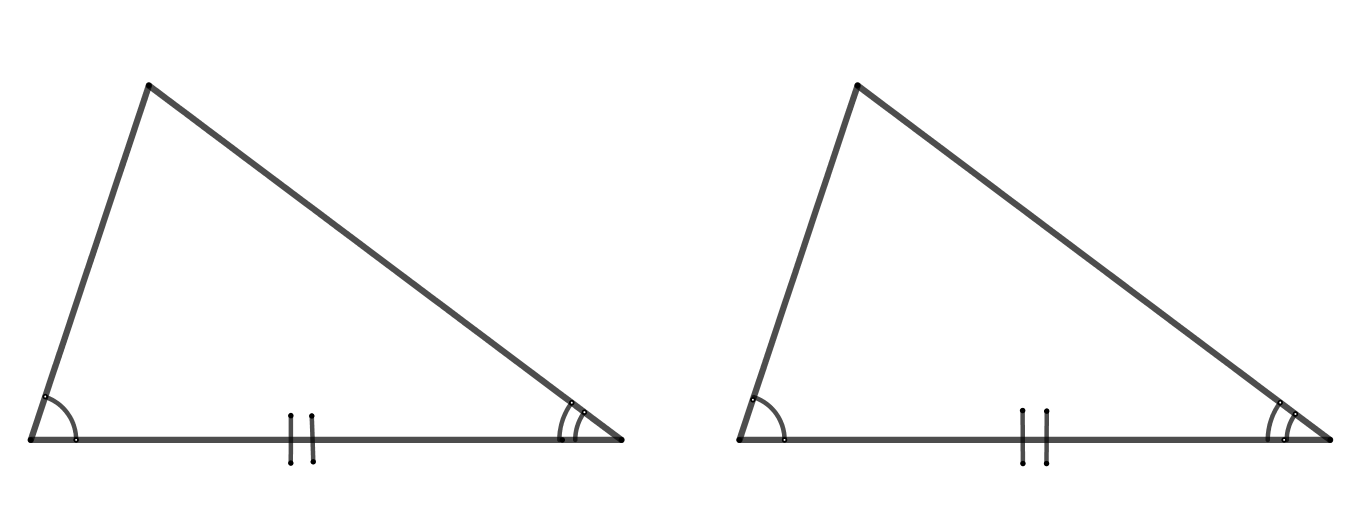
3 признак. По трем сторонам.
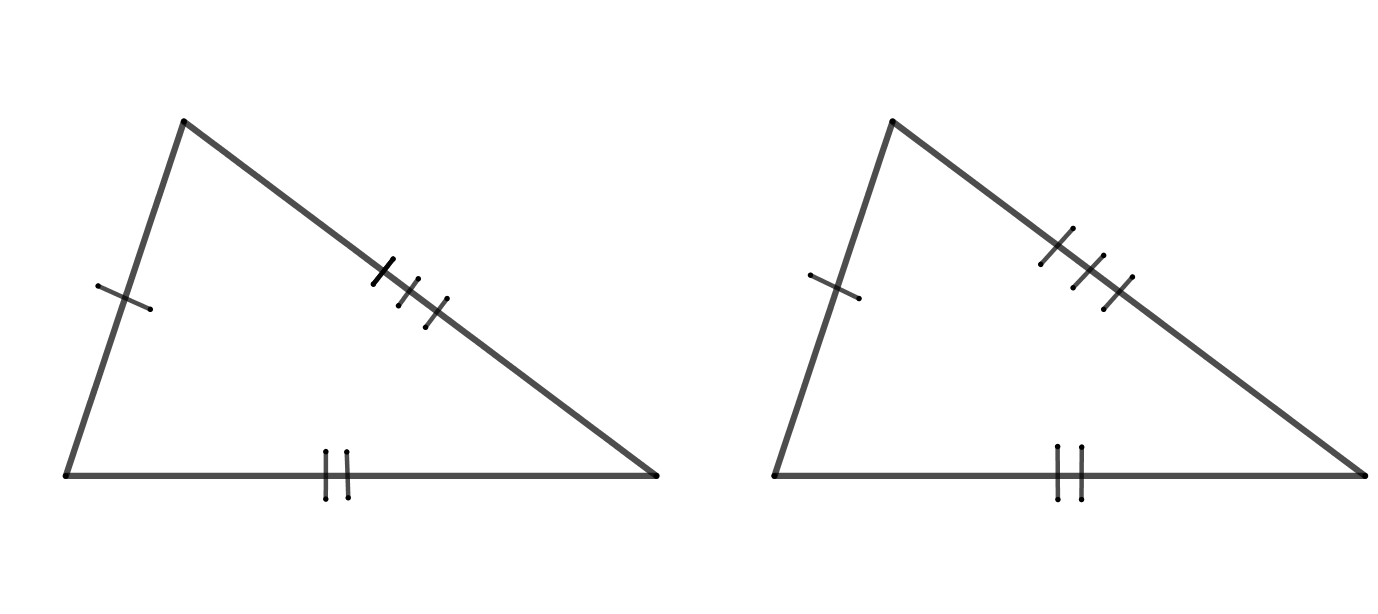
У равных треугольников все соответствующие элементы так же равны.
20. Площади подобных фигур относятся, как квадрат коэффициента подобия.
\(\dfrac{S_1}{S_2}=k^2\), где \(k\) - коэффициент подобия треугольников
21. Площадь прямоугольника
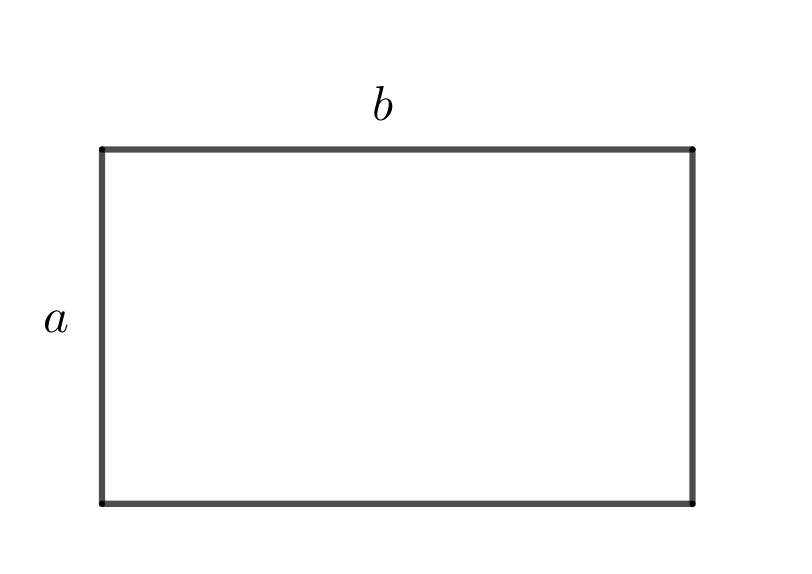
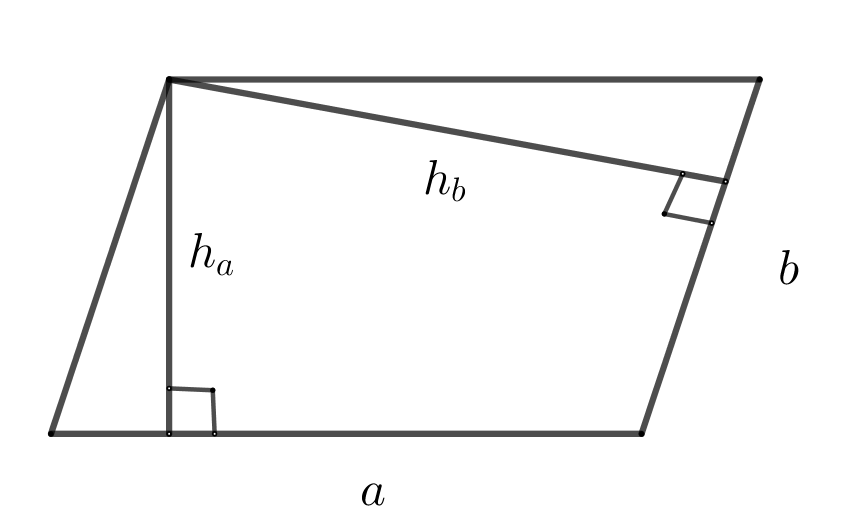
22. Площадь параллелограмма через сторону и высоту, проведенную к ней.
\(S=h_a\cdot a=h_b\cdot b\)
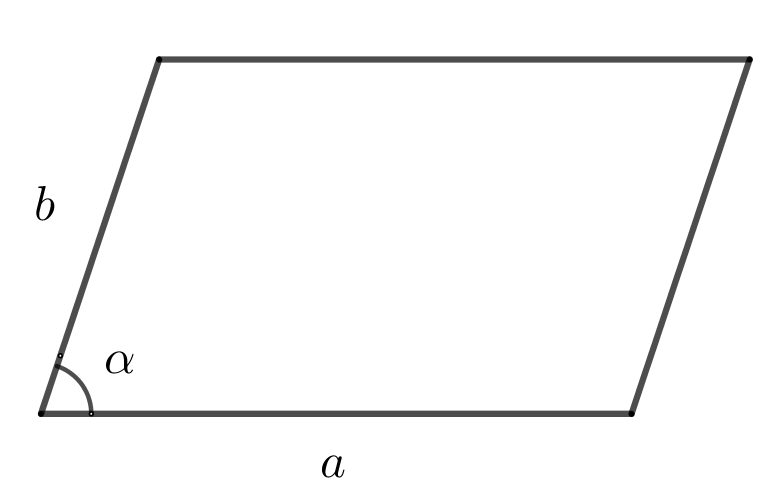
23. Площадь параллелограмма через две стороны и угол.
\(S=a\cdot b \sin \alpha\)
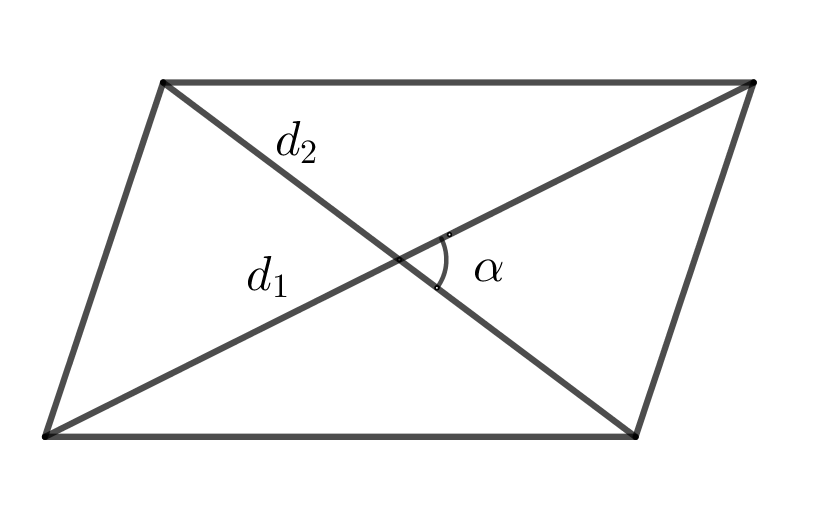
24. Площадь параллелограмма через диагонали и угол между ними
\(S=\dfrac{d_1\cdot d_2\sin \alpha}{2}\)
25. Площадь ромба через диагонали.
\(S=\dfrac{d_1\cdot d_2}{2}\)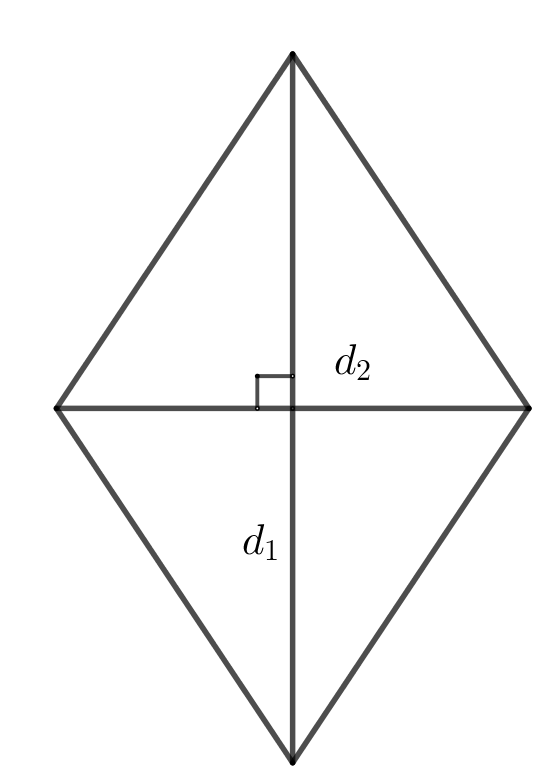
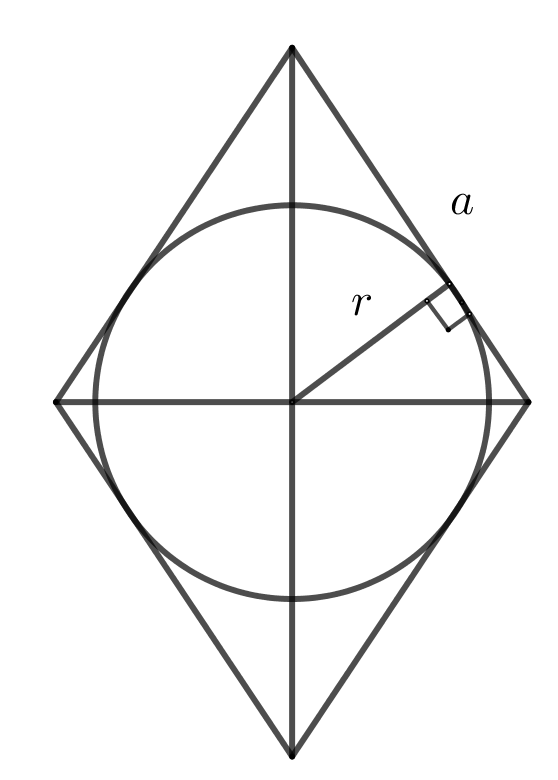
26. Площадь ромба через радиус вписанной окружности
\(S=a\cdot 2r\)
27. Площадь трапеции
\(S=\dfrac{(a+b)\cdot h}{2}\)
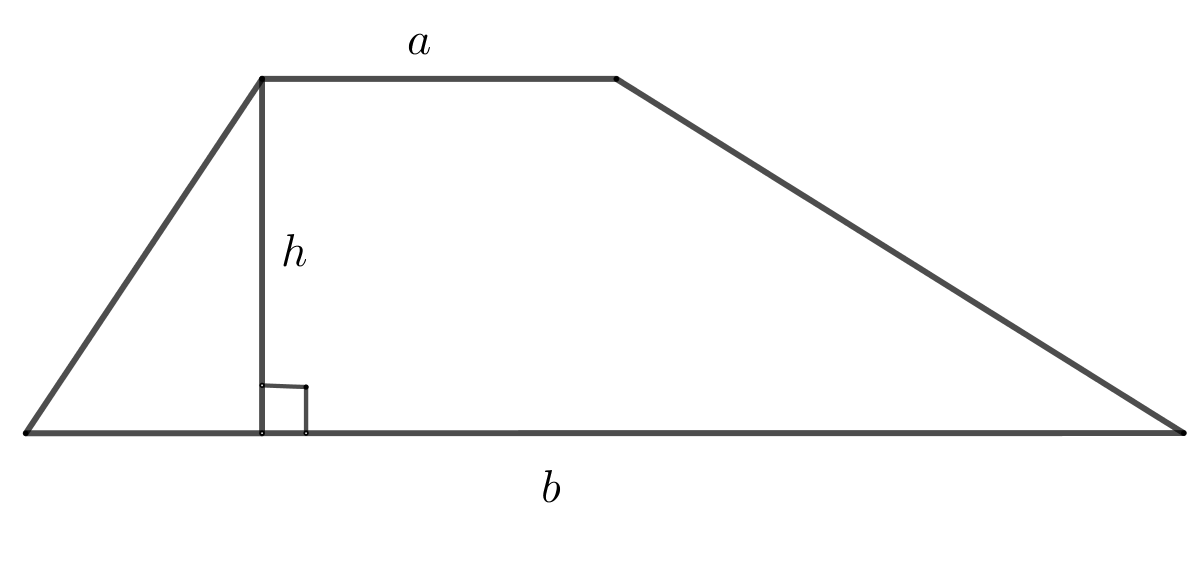
28. Средняя линия
\(KL=\dfrac{a+b}{2}\)
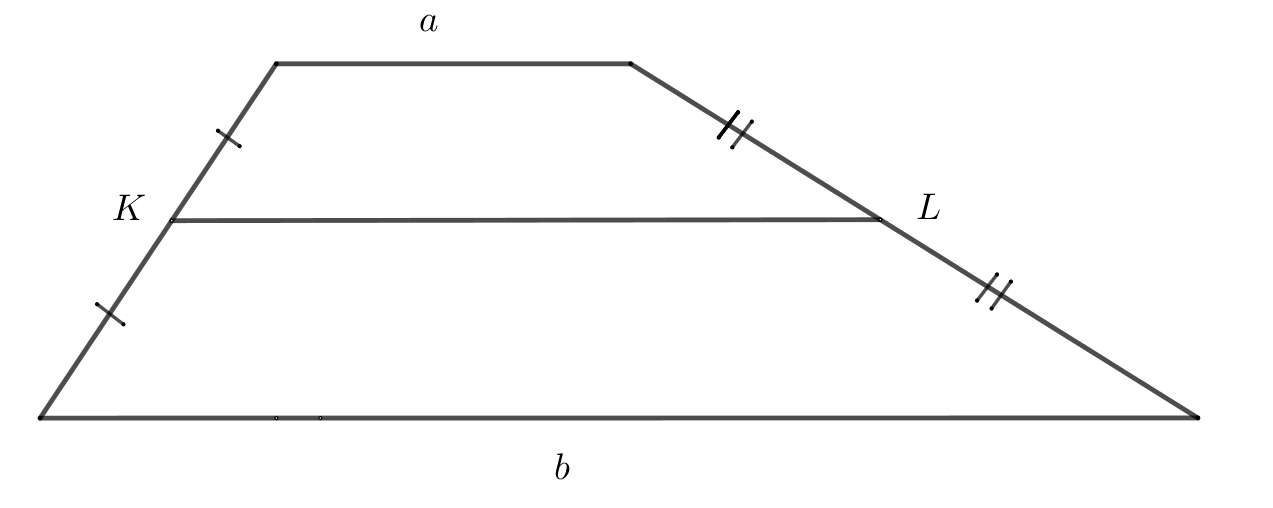
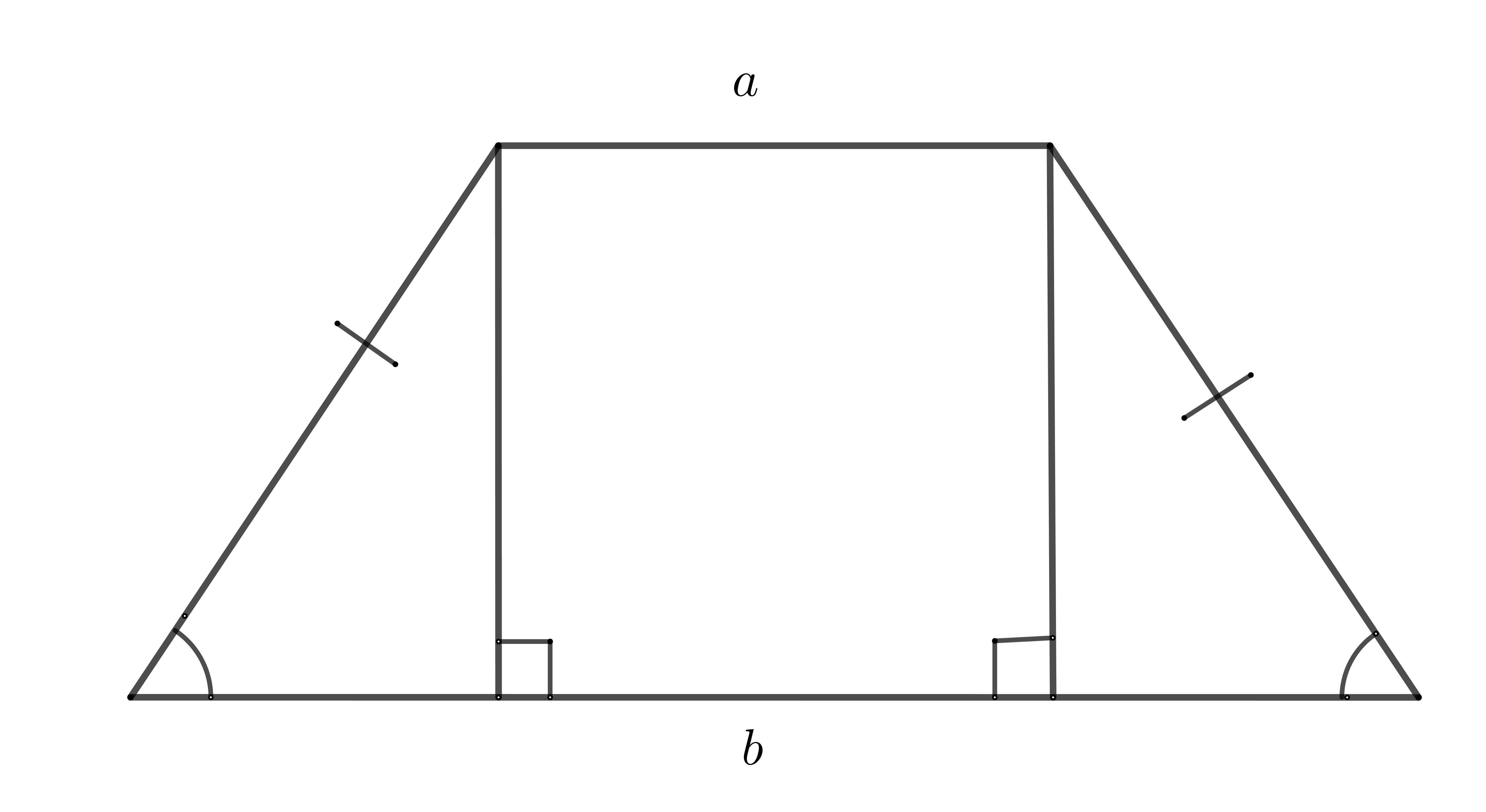
29. Равнобедренная трапеция.
Боковые стороны и углы при основании равны.
Можно провести две высоты, они отсекают два равных прямоугольных треугольника.
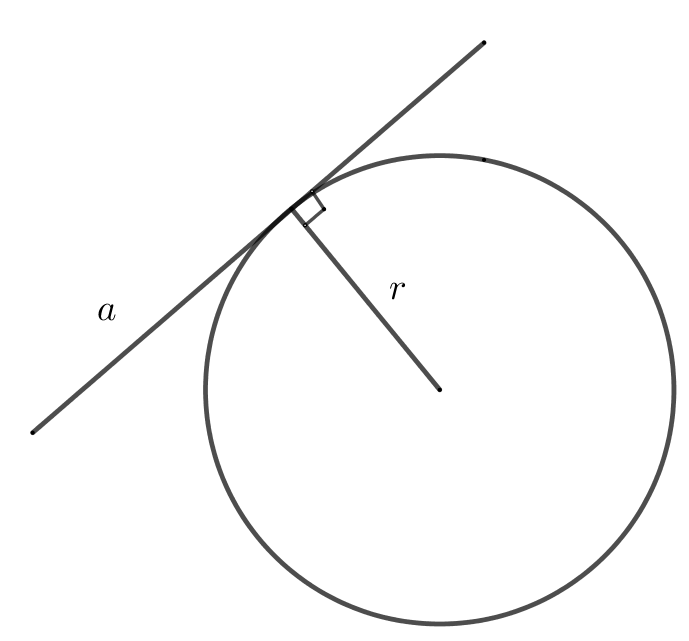
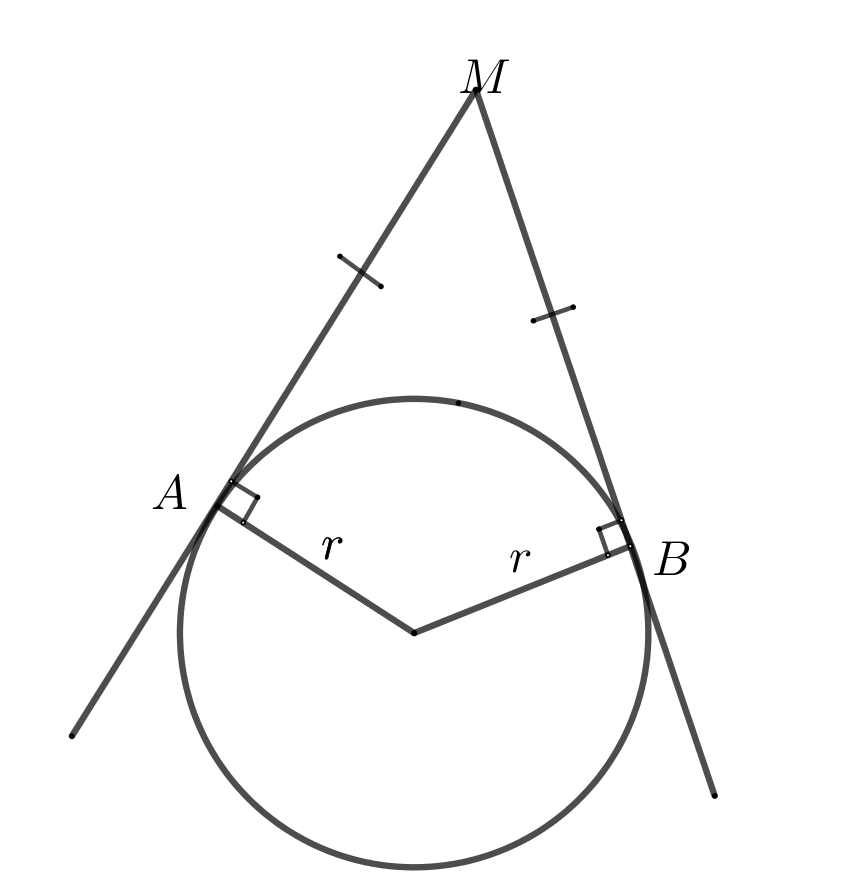
30. Радиус проведенный в точку касания касательной образует угол \(90^o\)
31. Касательные проведенные к окружности из одной точки равны.
Демо-доступ к платформе https://marseltutor.ru/
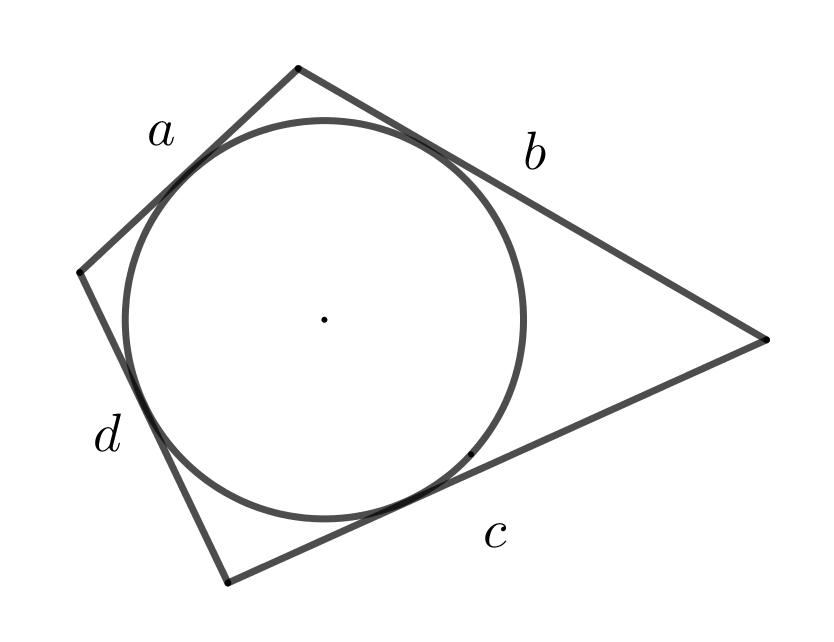
32. В четырехугольник можно вписать окружность, если суммы противоположных сторон равны.
Если в четырехугольник вписана окружность,значит сумма противоположных сторон равна.
33. Если около четырехугольника можно описать окружность, значит сумма противоположных углов равна \(180^o\)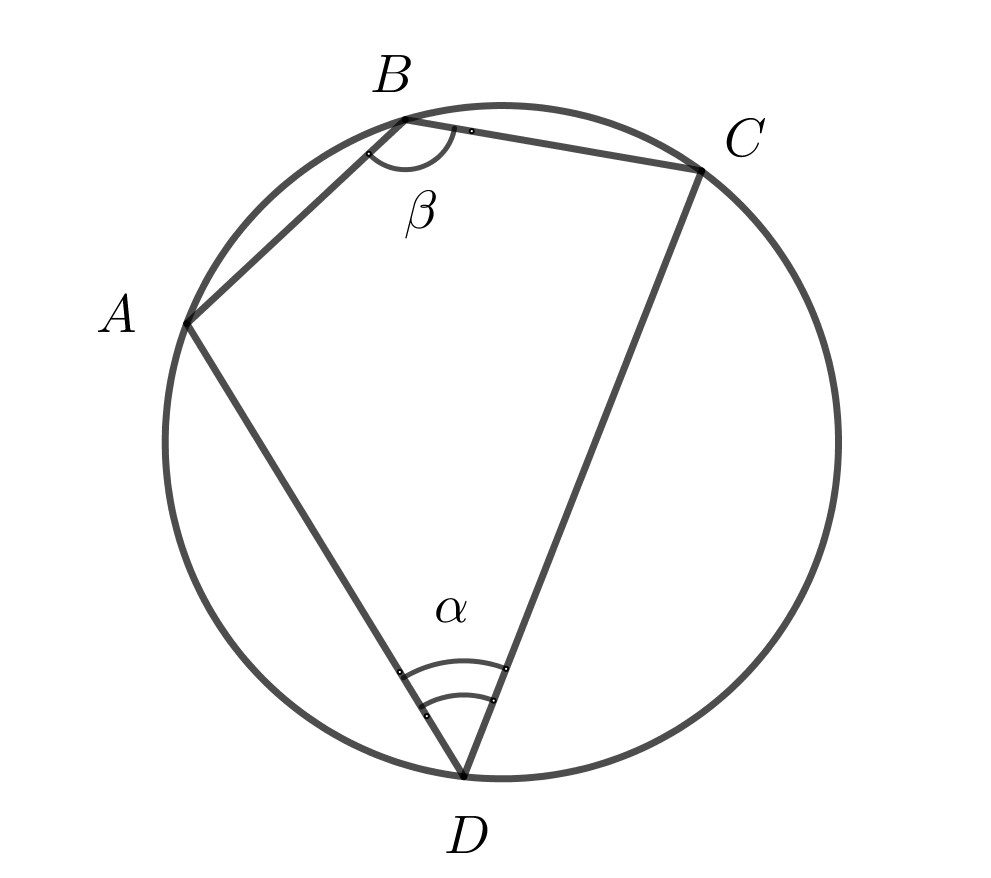
34. Вписанные углы равны половине дуги на которую опираются.
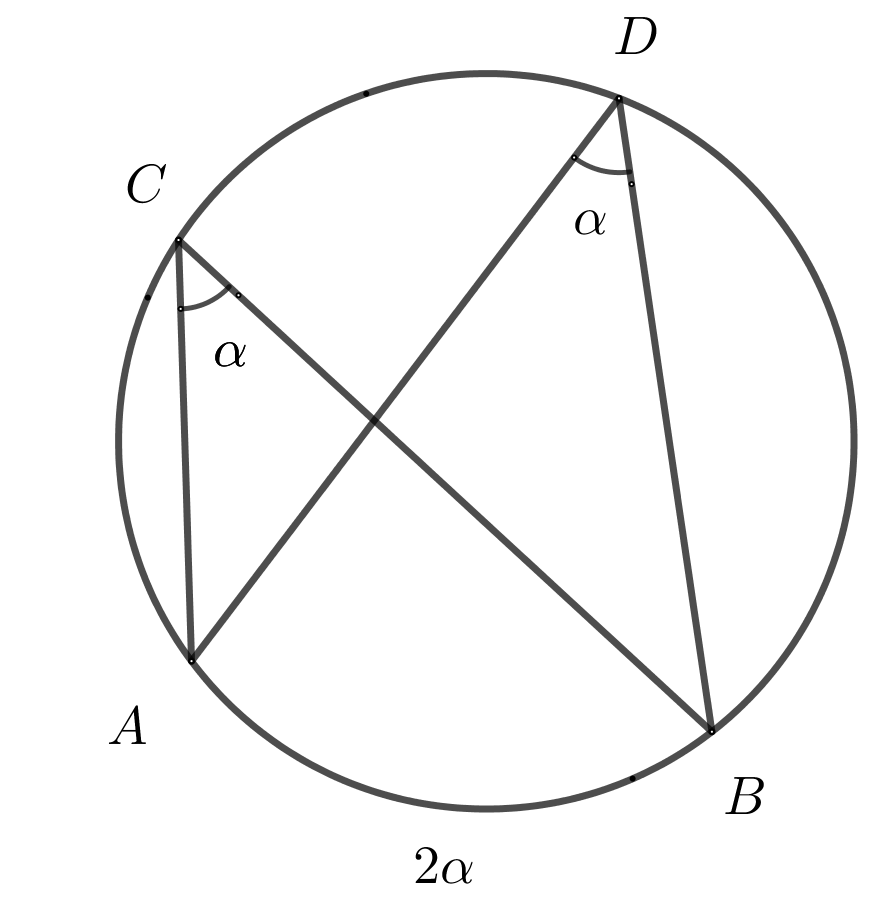
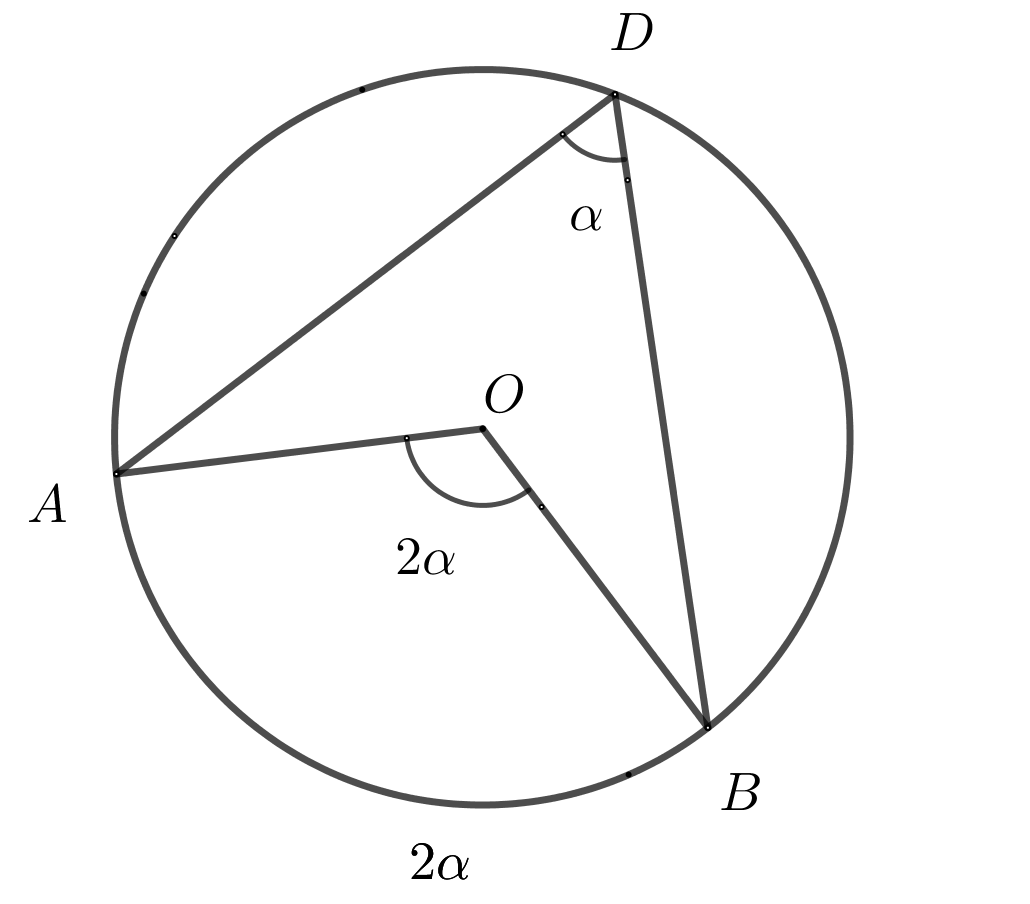
35. Вписанный угол в два раза меньше центрального угла, если они опираются на одну и ту же дугу.
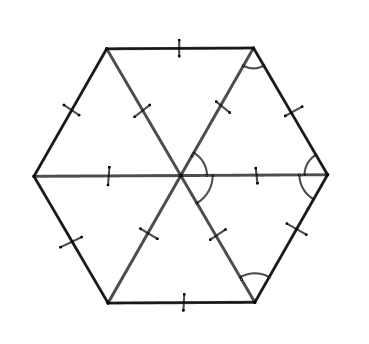
36. Правильный шестиугольник состоит из 6 правильных треугольников.
Радиус описанной окружности равен стороне шестиугольника
Радиус вписанной окружности равен высоте одного из 6 правильных треугольников
Все углы правильного шестиугольника равны \(120^o\)
37. Площадь многоугольника, в который вписана окружность
\(S=p\cdot r\),
где \(p=\dfrac{a+b+c+d+e+f}{2}\) - полупериметр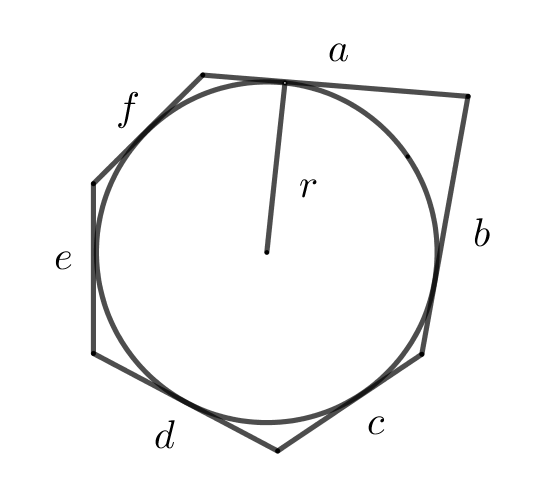
38. Площадь круга
\(S=\pi R^2\)
39. Длина окружности
\(l=2\pi R\)
Автор: Нуртдинов Марсель - преподаватель по математике
Узнать про курс подготовки к ЕГЭ по профильной математике напишите мне в телеграмм @Marseltutor