Исходное уравнение равносильно уравнению \(\sqrt{x-a} \cdot(\sin x-\cos x)=0\) .

Рассмотрим два случая. Первый случай: \(\sqrt{x-a}=0\).
Получаем \(x=a\).

Второй случай: \(\sin x-\cos x=0\) при условии \(x \geq a\).
Это уравнение имеет на отрезке \([0 ; \pi]\) единственный корень \(x=\dfrac{\pi}{4}\). Условие принимает вид \(\dfrac{\pi}{4} \geq a\). То есть в этом случае \(x=\dfrac{\pi}{4}\) при \(a \leq \dfrac{\pi}{4}\).

Корень уравнения \(x=a\) принадлежит отрезку \([0 ; \pi]\) при \(0 \leq a \leq \pi\).
Корни уравнения \(x=a\) и \(x=\dfrac{\pi}{4}\) совпадают при \(a=\dfrac{\pi}{4}\).

Таким образом, исходное уравнение имеет на отрезке \([0 ; \pi]\) ровно один корень при \(a<0\) и \(\dfrac{\pi}{4} \leq a \leq \pi\).

Запишем первое уравнение в виде \(\dfrac{(y-2)(x y-4)}{\sqrt{4-y}}=0\).

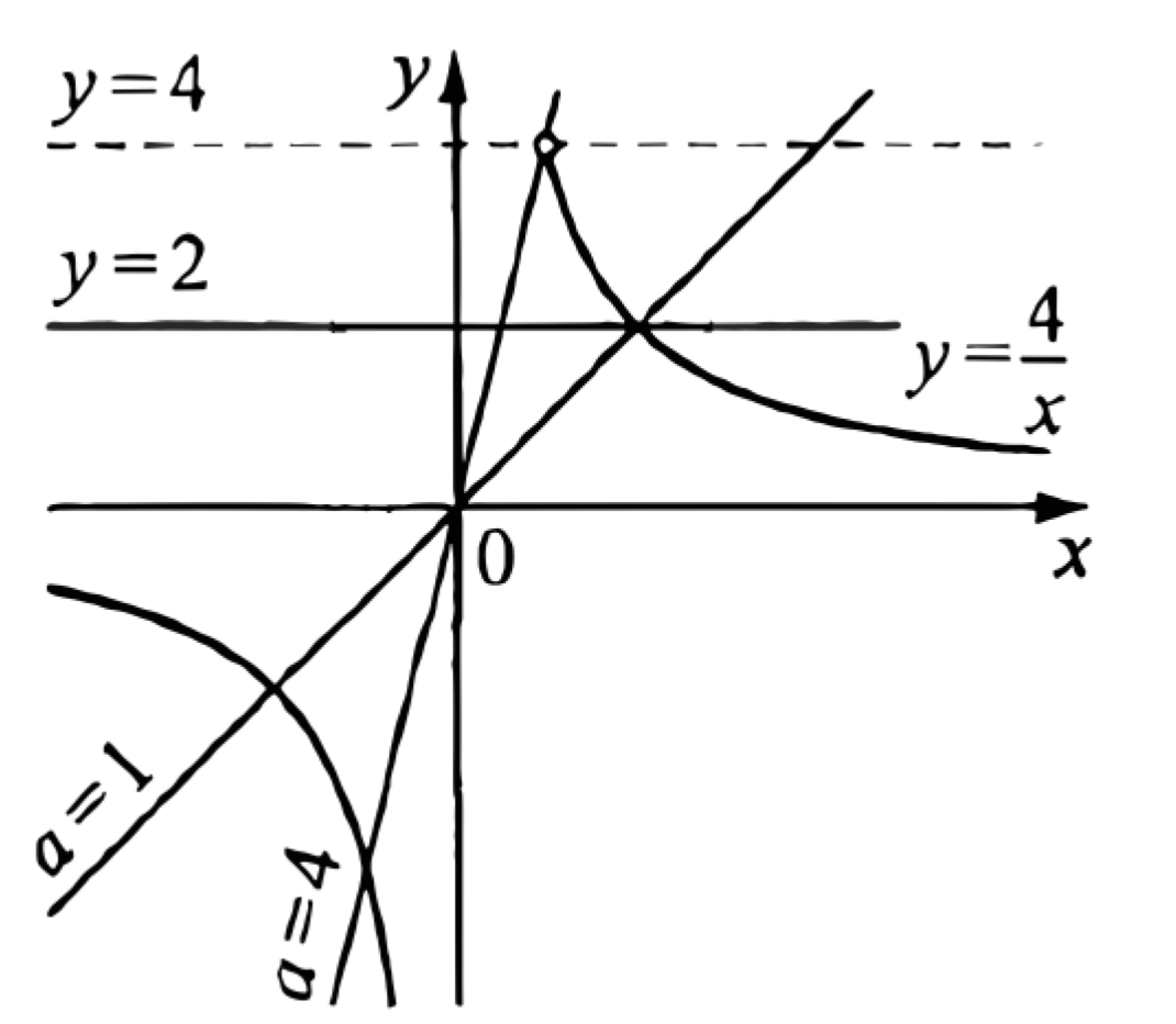
При \(y \geq 4\) левая часть этого уравнения не имеет смысла. При \(y<4\) уравнение задаёт прямую \(y=2\) и часть гиперболы \(y=\dfrac{4}{x}\), лежащую в полуплоскости \(y<4\) (см. рисунок).

При каждом значении \(a\) уравнение \(y=a x\) задаёт прямую с угловым коэффициентом \(a\), проходящую через начало координат.

При \(y<4\) прямая \(y=a x\) пересекает прямую \(y=2\) при любом ненулевом значении \(a\), пересекает часть правой ветви гиперболы \(y=\dfrac{4}{x}\), лежащую в полуплоскости \(y<4\), при \(0<a<4\), пересекает левую ветвь гиперболы \(y=\dfrac{4}{x}\) при \(a>0\). 

При этом прямая \(y=a x\) проходит через точку пересечения прямой \(y=2\) и гиперболы \(y=\dfrac{4}{x}\) при \(a=1\).

Число решений исходной системы равно числу точек пересечения прямой \(y=2\) и гиперболы \(y=\dfrac{4}{x}\) с прямой \(y=a x,\) лежащих в полуплоскости \(y<4\).

Таким образом, исходная система имеет ровно три различных решения при
\(0<a<1 ; 1<a<4 \text {. }\)

При \(x \leq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-a x-2 x^2-6 a+3 x-9 x=0 ; \\
a^2-a x-2 x^2-6 a-6 x=0 ; \\
(a-2 x)(a+x)-6(a+x)=0 ; \\
(a-2 x-6)(a+x)=0 .
\end{gathered}
\end{equation*}

Получившееся уравнение задаёт на плоскости Oхa пару лучей: луч \(l_1\)
с началом в точке \((0 ; 6)\), совпадающий
с прямой \(a=2 x+6\) при \(x \leq 0\), и луч \(l_2\) с началом в точке \((0 ; 0)\), совпадающий с прямой \(a=-x\) при \(x \leq 0\). Лучи \(l_1\) и \(l_2\) пересекаются в точке \((-2 ; 2)\).

При \(x \geq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-a x-2 x^2-6 a+3 x+9 x=0 ; \\
a^2-a x-2 x^2-6 a+12 x=0 ; \\
(a-2 x)(a+x)-6(a-2 x)=0 ;\\
(a-2 x)(a+x-6)=0.
\end{gathered}
\end{equation*}

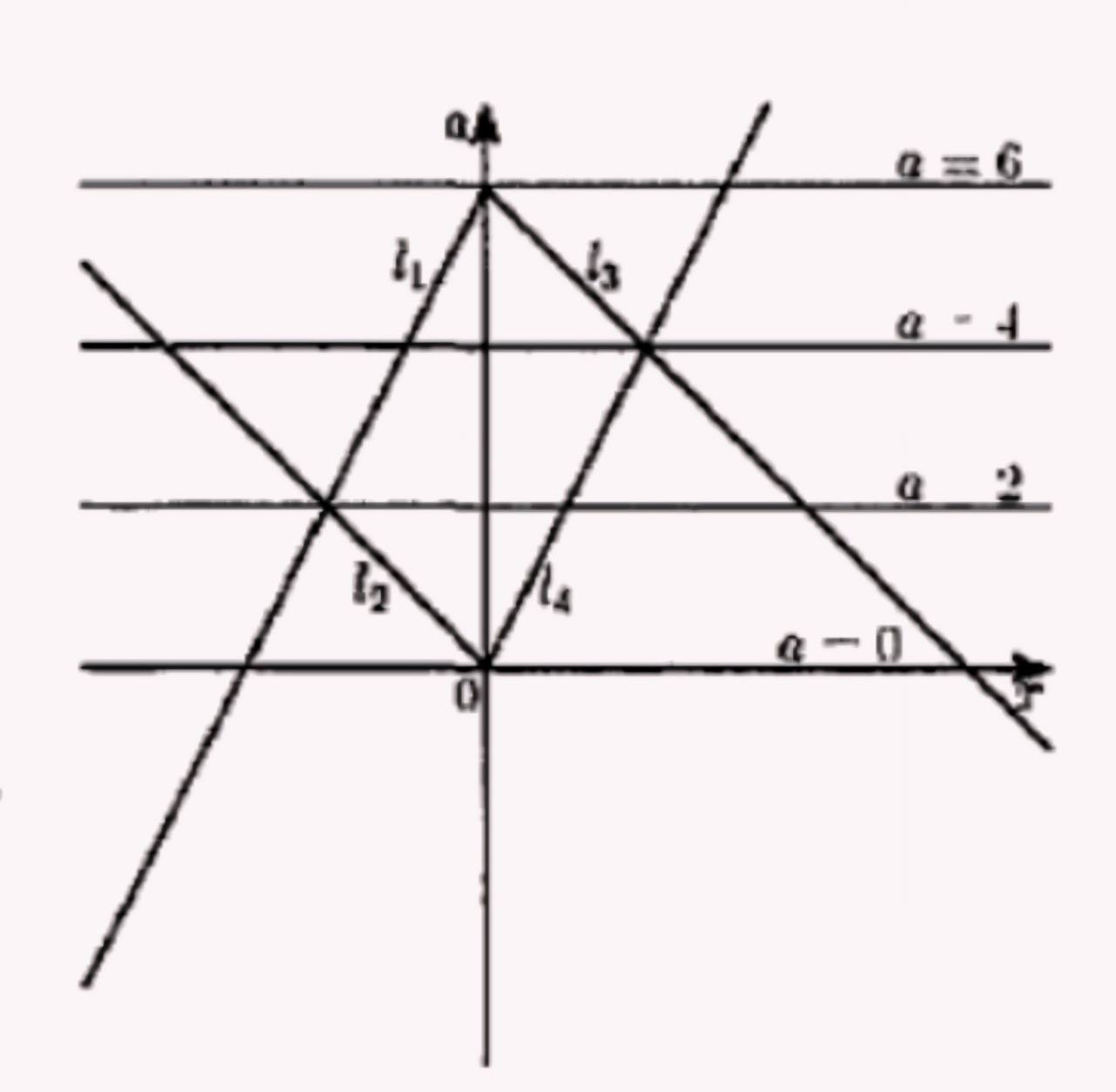
Получившееся уравнение задаёт на плоскости Оха пару лучей: луч \(l_3\) с началом в точке \((0 ; 6)\), совпадающий с прямой \(a=6-x\) при \(x \geq 0\), и луч \(l_4\) с началом в точке \((0 ; 0)\), совпадающий с прямой \(a=2 x\) при \(x \geq 0\). Лучи \(l_3\) и \(l_4\) пересекаются в точке \((2 ; 4)\).

Число корней исходного уравнения равно числу точек пересечения прямой \(a=c\) с объединением лучей \(l_1, l_2, l_3\) и \(l_4\).

Каждый из лучей \(l_1\) и \(l_3\) пересекается с прямой \(a=c\) в одной точке при \(c \leq 6\) и не пересекается при \(c>6\).

Каждый из лучей \(l_2\) и \(l_4\) пересекается с прямой \(a=c\) в одной точке при \(c \geq 0\) и не пересекается при \(c<0\).

Следовательно, при \(a<0\) и \(a>6\) исходное уравнение имеет два различных корня.

При \(c=0, c=2, c=4\) и \(c=6\) прямая \(a=c\) проходит через общую точку лучей \(l_2\) и \(l_4, l_1\) и \(l_2, l_3\) и \(l_4, l_1\) и \(l_3\) соответственно.

Следовательно, при \(a=0, a=2, a=4\) и \(a=6\) исходное уравнение имеет ровно три корня, а при \(0<a<2,2<a<4\) и \(4<a<6\) имеет четыре различных корня.

При \(x<-a \quad\) уравнение \(\left|x^2+a^2-6 x-4 a\right|=2 x+2 a\) не имеет корней, поскольку его левая часть принимает неотрицательные значения, а правая - отрицательные.

При \(\quad x \geq-a \quad\) уравнение \(\left|x^2+a^2-6 x-4 a\right|=2 x+2 a\) равносильно совокупности двух уравнений:
\(x^2+a^2-6 x-4 a =2 x+2 a   и\)

\( x^2+a^2-6 x-4 a =-2 x-2 a .\)

При \(x \geq-a\)
уравнение \(x^2+a^2-6 x-4 a=2 x+2 a\) принимает вид:

\(x^2+a^2-8 x-6 a=0; \)

\((x-4)^2+(a-3)^2=25.\)

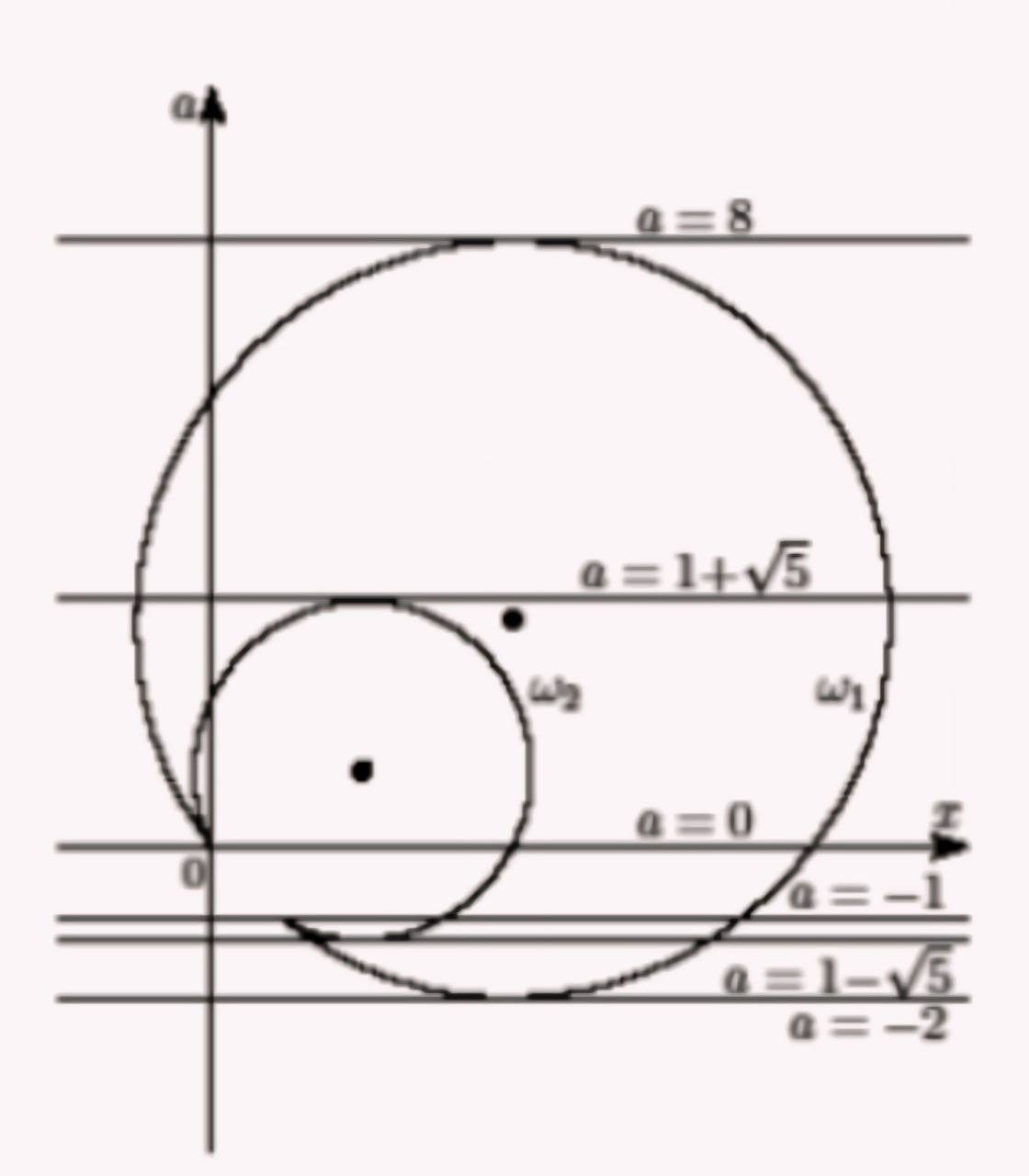
Получившееся уравнение задаёт на плоскости Оха дугу \(\omega_1\) окружности с центром в точке \((4 ; 3)\) радиусом 5 , лежащую в полуплоскости \(a \geq-x\), с концами в точках \((0 ; 0)\) и \((1 ;-1)\).

При \(x \geq-a\) уравнение \(x^2+a^2-6 x-4 a=-2 x-2 a\) принимает вид:
\(x^2+a^2-4 x-2 a=0 ;\)

\((x-2)^2+(a-1)^2=5 .\)

Получившееся уравнение задаёт на плоскости Оха дугу \(\omega_2\) окружности с центром в точке \((2 ; 1)\) радиусом \(\sqrt{5}\), лежащую в полуплоскости \(a \geq-x\), с концами в точках \((0 ; 0)\) и \((1 ;-1)\).

Число корней исходного уравнения равно числу точек пересечения прямой \(a=c\) с объединением дуг \(\omega_1\) и \(\omega_2\).

Дуга \(\omega_1\) пересекается с прямой \(a=c\) в двух точках при \(-2<c \leq-1\) и \(0 \leq c<8\), в одной точке при \(c=-2,-1<c<0\) и \(c=8\) и не пересекается при \(c<-2\) и \(c>8\).

Дуга \(\omega_2\) пересекается с прямой \(a=c\) в двух точках при \(1-\sqrt{5}<c \leq-1\) и \(0 \leq c<1+\sqrt{5}\), в одной точке при \(c=1-\sqrt{5}, \quad-1<c<0\) и \(c=1+\sqrt{5}\) и не пересекается при \(c<1-\sqrt{5}\) и \(c>1+\sqrt{5}\).

При \(c=-1\) и при \(c=0\) прямая \(a=c\) проходит через общую точку дуг \(\omega_1\) и \(\omega_2\).
Следовательно, исходное уравнение имеет четыре различных корня при \(1-\sqrt{5}<a<-1\) и \(0<a<1+\sqrt{5}\).

При \(x \leq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-4 x^2-8 x-4=0 ; \\
a^2-(2 x+2)^2=0 \\
(a-2 x-2)(a+2 x+2)=0 .
\end{gathered}
\end{equation*}

Получившееся уравнение задаёт
на плоскости Oхa пару лучей: луч \(l_1\)
с началом в точке \((0 ; 2)\), совпадающий
с прямой \(a=2 x+2\) при \(x \leq 0\), и луч \(l_2\)
с началом в точке \((0 ;-2)\), совпадающий
с прямой \(a=-2 x-2\) при \(x \leq 0\). 
Лучи \(l_1\)
и \(l_2\) пересекаются в точке \((-1 ; 0)\).

При \(x \geq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-4 x^2+8 x-4=0 ; \\
a^2-(2 x-2)^2=0 ;\\
(a-2 x+2)(a+2 x-2)=0 .
\end{gathered}
\end{equation*}

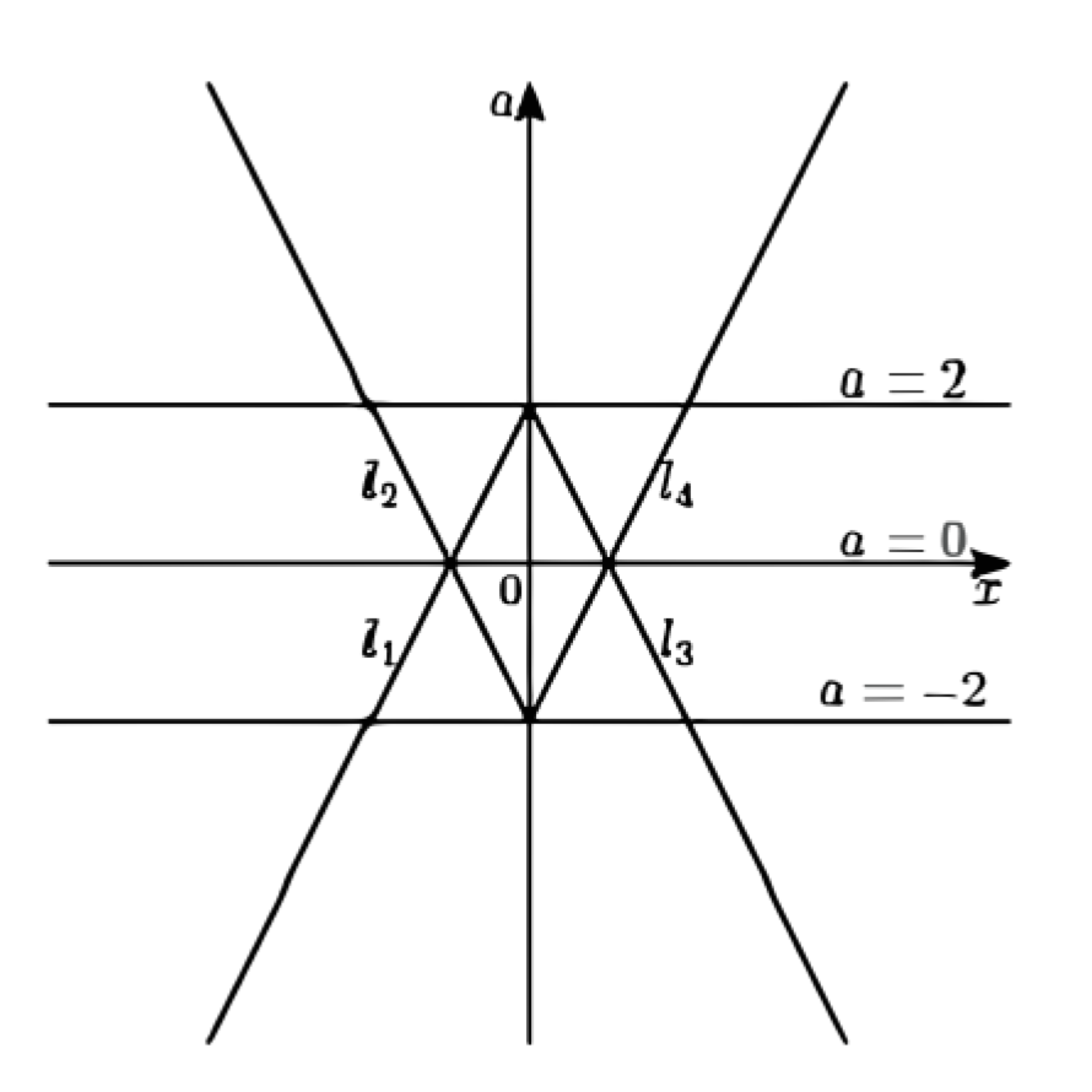
Получившееся уравнение задаёт на плоскости Оха пару лучей: луч \(l_3\) с началом в точке \((0 ; 2)\), совпадающий с прямой \(a=2-2 x\) при \(x \geq 0\), и луч \(l_4\) с началом в точке \((0 ;-2)\), совпадающий с прямой \(a=2 x-2\) при \(x \geq 0\). 

Лучи \(l_3\) и \(l_4\) пересекаются в точке \((1 ; 0)\).

Число корней исходного уравнения равно числу точек пересечения прямой \(a=c\) с объединением лучей \(l_1, l_2, l_3\) и \(l_4\).
Каждый из лучей \(l_1\) и \(l_3\) пересекается с прямой \(a=c\) в одной точке при \(c \leq 2\) и не пересекается при \(c>2\).

Каждый из лучей \(l_2\) и \(l_4\) пересекается с прямой \(a=c\) в одной точке при \(c \geq-2\) и не пересекается при \(c<-2\).
Следовательно, при \(a<-2\) и \(a>2\) исходное уравнение имеет ровно два различных корня.

При \(c=-2\) и при \(c=2\) прямая \(a=c\) проходит через общую точку лучей \(l_2\) и \(l_4, l_1\) и \(l_3\) соответственно. Значит, при \(a=-2\) и \(a=2\) исходное уравнение имеет ровно три корня.

При \(c=0\) прямая \(a=c\) проходит через точки пересечения лучей \(l_3\) и \(l_4\), \(l_1\) и \(l_2\). Значит, при \(a=0\) исходное уравнение имеет ровно два корня.

Следовательно, при \(-2<a<0\) и \(0<a<2\) исходное уравнение имеет ровно четыре корня.

Таким образом, исходное уравнение имеет ровно два различных корня при \(a<-2, a=0\) и \(a>2\).

При \(x \leq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-x^2-2 x-1=0 ; \\
a^2-(x+1)^2=0 ; \\
(a-x-1)(a+x+1)=0 .
\end{gathered}
\end{equation*}

Получившееся уравнение задаёт на плоскости Oхa пару лучей: луч \(l_1\)
с началом в точке \((0 ; 1)\), совпадающий с прямой \(a=x+1\) при \(x \leq 0\), и луч \(l_2\) с началом в точке \((0 ;-1)\), совпадающий
с прямой \(a=-x-1\) при \(x \leq 0\). 

Лучи \(l_1\) и \(l_2\) пересекаются в точке \((-1 ; 0)\).

При \(x \geq 0\) уравнение принимает вид:
\begin{equation*}
\begin{gathered}
a^2-x^2+2 x-1=0 ; \\
a^2-(x-1)^2=0 ; \\
(a-x+1)(a+x-1)=0 .
\end{gathered}
\end{equation*}
Получившееся уравнение задаёт на плоскости Оха пару лучей: луч \(l_3\) с началом в точке \((0 ; 1)\), совпадающий с прямой \(a=1-x\) при \(x \geq 0\), и луч \(l_4\) с началом в точке \((0 ;-1)\), совпадающий с прямой \(a=x-1\) при \(x \geq 0\). 

Лучи \(l_3\) и \(l_4\) пересекаются в точке \((1 ; 0)\).

Число корней исходного уравнения равно числу точек пересечения прямой \(a=c\) с объединением лучей \(l_1, l_2, l_3\) и \(l_4\).

Каждый из лучей \(l_1\) и \(l_3\) пересекается с прямой \(a=c\) в одной точке при \(c \leq 1\) и не пересекается при \(c>1\).

Каждый из лучей \(l_2\) и \(l_4\) пересекается с прямой \(a=c\) в одной точке при \(c \geq-1\) и не пересекается при \(c<-1\).

Следовательно, при \(a<-1\) и \(a>1\) исходное уравнение имеет ровно два корня.

При \(c=-1\) и \(c=1\) прямая \(a=c\) проходит через общую точку лучей \(l_2\) и \(l_4\), \(l_1\) и \(l_3\) соответственно. Значит, при \(a=-1\) и \(a=1\) исходное уравнение имеет ровно три корня.

При \(c=0\) прямая \(a=c\) проходит через точки пересечения лучей \(l_3\) и \(l_4\), \(l_1\) и \(l_2\). Значит, при \(a=0\) исходное уравнение имеет ровно два корня.

Следовательно, при \(-1<a<0\) и \(0<a<1\) исходное уравнение имеет ровно четыре корня.

Таким образом, исходное уравнение имеет ровно два различных корня при \(a<-1, a=0\) и \(a>1\).