18. Задачи с параметром
Чтобы получить дополнительный функционал нужно войти.
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых система уравнений
\begin{equation*}
\left\{\begin{array}{l}
\left(x^2+y^2+4 x\right) \cdot \sqrt{2 x+y+6}=0, \\
y=a x-2 a
\end{array}\right.
\end{equation*}
имеет ровно два различных решения.
Решение
Каждое решение уравнения \(\left(x^2+y^2+4 x\right) \cdot \sqrt{2 x+y+6}=0\) либо является решением уравнения \(2 x+y+6=0\), откуда \(y=-2 x-6\), либо является решением уравнения \(x^2+y^2+4 x=0\) при условии \(2 x+y+6 \geq 0\).
Для каждого из этих случаев подставим \(y=a x-2 a\) и найдём количество корней получившегося уравнения в зависимости от \(a\).
Первый случай: \(a x-2 a=-2 x-6\), откуда при \(a \neq-2\) получаем: \(x=\dfrac{2 a-6}{a+2}\).
При \(a=-2\) корней нет.
Второй случай: \(x^2+(a x-2 a)^2+4 x=0\) при условии \((a+2) x \geq 2 a-6\).
Получаем квадратное уравнение \(\left(a^2+1\right) x^2+\left(4-4 a^2\right) x+4 a^2=0\). Дискриминант этого уравнения равен
\(\left(4 a^2-4\right)^2-16\left(a^4+a^2\right)=-48 a^2+16=\)
\(-16(\sqrt{3} \cdot a-1)(\sqrt{3} \cdot a+1)\).
Значит, уравнение \(\left(a^2+1\right) x^2+\left(4-4 a^2\right) x+4 a^2=0\) имеет два корня при \(-\dfrac{\sqrt{3}}{3}<a<\dfrac{\sqrt{3}}{3}\), имеет единственный корень \(x=\dfrac{2 a^2-2}{a^2+1}\) при \(a=-\dfrac{\sqrt{3}}{3}\) и при \(a=\dfrac{\sqrt{3}}{3}\) и не имеет корней при \(a<-\dfrac{\sqrt{3}}{3}\) и при \(a>\dfrac{\sqrt{3}}{3}\).
Функция \(f(x)=\left(a^2+1\right) x^2+\left(4-4 a^2\right) x+4 a^2 \) принимает наименьшее значение при \(x=\dfrac{2 a^2-2}{a^2+1}\). Подставив \(x=\dfrac{2 a^2-2}{a^2+1}\) в условие \((a+2) x \geq 2 a-6\), получаем:
\((a+2) \cdot \dfrac{2 a^2-2}{a^2+1} \geq 2 a-6 ; \)
\(2 a^3+4 a^2-2 a-4 \geq 2 a^3-6 a^2+2 a-6 ; \)
\(10 a^2-4 a+2 \geq 0 .\)
Это неравенство верно для любого \(a\). Следовательно, наибольший корень уравнения \(f(x)=0\) при \(-\dfrac{\sqrt{3}}{3}<a<\dfrac{\sqrt{3}}{3}\) удовлетворяет условию \((a+2) x \geq 2 a-6\), поскольку он не меньше, чем \(\dfrac{2 a^2-2}{a^2+1}\).
При \(-\dfrac{\sqrt{3}}{3}<a<\dfrac{\sqrt{3}}{3}\) меньший корень уравнения \(f(x)=0\) удовлетворяет условию \((a+2) x \geq 2 a-6\) тогда и только тогда, когда \(f\left(\dfrac{2 a-6}{a+2}\right) \geq 0\).
Значит: \(\left(a^2+1\right)\left(\dfrac{2 a-6}{a+2}\right)^2+\)
\(\left(4-4 a^2\right)\left(\dfrac{2 a-6}{a+2}\right)+4 a^2 \geq 0\)
\(\left(a^2+1\right)(2 a-6)^2+\left(4-4 a^2\right)(2 a-6)\)
\((a+2)+4 a^2(a+2)^2 \geq 0\)
\(112 a^2-32 a-12 \geq 0 ; \)
\(4(2 a-1)(14 a+3) \geq 0\)
откуда \(a \leq-\dfrac{3}{14} ; a \geq \dfrac{1}{2}\).
Число \(\dfrac{2 a-6}{a+2}\) является корнем квадратного уравнения \(f(x)=0\) при \(a=-\dfrac{3}{14}\) и при \(a=\dfrac{1}{2}\).
Таким образом, исходная система уравнений имеет ровно два различных решения при \(a=-\dfrac{\sqrt{3}}{3} ;-\dfrac{3}{14} \leq a \leq \dfrac{1}{2} ; a=\dfrac{\sqrt{3}}{3}\).
Ответ
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых система уравнений
\begin{equation*}
\left\{\begin{array}{l}
(|x+1|+|x-3|-y) \cdot \sqrt{10-x-y}=0, \\
y=x+a
\end{array}\right.
\end{equation*}
имеет ровно два различных решения.
Решение
Каждое решение уравнения \((|x+1|+|x-3|-y) \cdot \sqrt{10-x-y}=0\) либо является решением уравнения \(10-x-y=0\), откуда \(y=10-x\), либо является решением системы:
\begin{cases}
{ | x + 1 | + | x - 3 | - y = 0 } \\
{ 1 0 - x - y \geq 0 }
\end{cases}
\begin{cases}
{y=|x+1|+|x-3| } \\
{10-x-|x+1|-|x-3| \geq 0, }
\end{cases}
откуда \(y=|x+1|+|x-3|\) при условии \(-8 \leq x \leq 4\).
Для каждого из этих случаев подставим \(y=x+a\) и найдём количество корней получившегося уравнения в зависимости от \(a\).
Первый случай: \(x+a=10-x\), откуда \(x=\dfrac{10-a}{2}\).
Второй случай: \(x+a=|x+1|+|x-3|\) при условии \(-8 \leq x \leq 4\).
Рассмотрим функцию \( f(x)=|x+1|+|x-3|-x-a .\) Уравнение \(x+a=|x+1|+|x-3|\) равносильно уравнению \(f(x)=0\).
Функция \(f(x)\) убывает при \(x \leq 3\) и возрастает при \(x \geq 3\), следовательно, она принимает наименьшее значение при \(x=3\), и это значение равно \(1-a\). Тогда уравнение \(f(x)=0\) имеет два корня при \(a>1\), имеет единственный корень \(x=3\) при \(a=1\) и не имеет корней при \(a<1\).
При \(a>1\) больший корень уравнения \(f(x)=0\) удовлетворяет условию \(-8 \leq x \leq 4\) тогда и только тогда, когда \(f(4) \geq 0 ; 2-a \geq 0\), откуда \(a \leq 2\).
Аналогично меньший корень уравнения \(f(x)=0\) удовлетворяет условию \(-8 \leq x \leq 4\) тогда и только тогда, когда \(f(-8) \geq 0 ; 26-a \geq 0\), откуда \(a \leq 26\).
Число \(\dfrac{10-a}{2}\) является корнем уравнения \(f(x)=0\) при \(\left|\dfrac{12-a}{2}\right|+\left|\dfrac{4-a}{2}\right|-\dfrac{10-a}{2}-a=0\), то есть при \(a=2\) и при \(a=26\).
Таким образом, исходная система уравнений имеет ровно два различных решения при \(a=1 ; 2 \leq a<26\).
Ответ
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых система уравнений
\begin{equation*}
\left\{\begin{array}{l}
\left|x^2-1\right|-2 x-x^2=\left|y^2-1\right|-2 y-y^2 \\
x+y=a
\end{array}\right.
\end{equation*}
имеет больше двух решений.
Решение
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы. Рассмотрим четыре случая.
1) Если \(x^2-1 \leq 0\) и \(y^2-1 \leq 0\), то получаем уравнение:
\begin{equation*}
\begin{gathered}
1-x^2-2 x-x^2=1-y^2-2 y-y^2 ; \\
y^2-x^2+y-x=0 ;(y-x)(x+y+1)=0 .
\end{gathered}
\end{equation*}
Полученное уравнение задаёт пару прямых \(y=x\) и \(x+y=-1\).
2) Если \(x^2-1 \leq 0\) и \(y^2-1 \geq 0\), то получаем уравнение:
\(1-x^2-2 x-x^2=y^2-1-2 y-y^2 ;\)
\(y=x^2+x-1 .\)
Полученное уравнение задаёт параболу \(y=x^2+x-1\).
3) Если \(x^2-1 \geq 0\) и \(y^2-1 \leq 0\), то получаем уравнение:
\(x^2-1-2 x-x^2=1-y^2-2 y-y^2 ;\)
\(x=y^2+y-1 .\)
Полученное уравнение задаёт параболу \(x=y^2+y-1\).
4) Если \(x^2-1 \geq 0\) и \(y^2-1 \geq 0\), то получаем уравнение:
\begin{equation*}
x^2-1-2 x-x^2=y^2-1-2 y-y^2 ; y=x .
\end{equation*}
Полученное уравнение задаёт прямую \(y=x\).
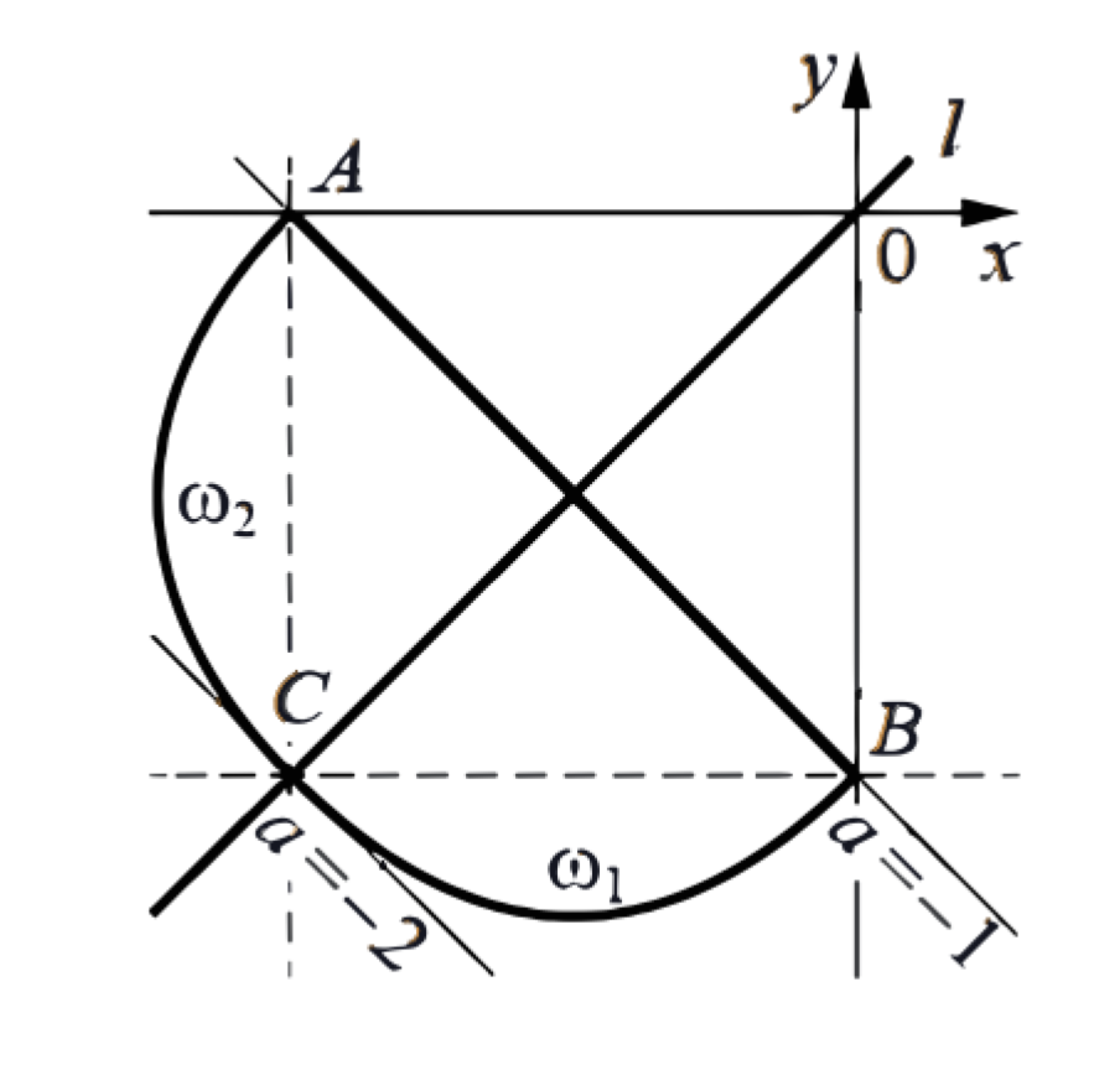
Точки \(A(-1 ; 0), B(0 ;-1)\) и \(C(-1 ;-1)\) являются точками пересечения полученных парабол с полученными прямыми и лежат на прямых \(x=-1\) и/или \(y=-1\), поэтому искомое множество состоит из прямой \(l\), задаваемой уравнением \(y=x\), отрезка \(A B\) прямой \(x+y=-1\), дуги \(\omega_1\) параболы \(y=x^2+x-1\) с концами в точках \(B\) и \(C\) и дуги \(\omega\), параболы \(x=y^2+y-1\) с концами в точках \(A\) и \(C\) (см. рис.).
Рассмотрим второе уравнение системы. Оно задаёт прямую \(m\), параллельную прямой \(A B\) или совпадающую с ней.
Заметим, что при \(a=-2\) прямая \(m\) касается парабол \(x=y^2+y-1\) и \(y=x^2+x-1\) в точке \(C\).
При \(a=-1\) прямая \(m\) содержит отрезок \(A B\), то есть исходная система имеет бесконечное число решений.
При \(a=-2\) прямая \(m\) касается дуг \(\omega_1\) и \(\omega_2\) в точке \(C\), пересекает прямую \(l\) в точке \(C\) и не пересекает отрезок \(A B\), то есть исходная система имеет одно решение.
При \(-2<a<-1\) прямая \(m\) не пересекает отрезок \(A B\), пересекает прямую \(l\) в точке, отличной от точки \(C\), и пересекает каждую из дуг \(\omega_1\) и \(\omega_2\) в одной точке, отличной от точки \(C\), то есть исходная система имеет три решения.
При \(a<-2\) или \(a>-1\) прямая \(m\) пересекает прямую \(l\) в одной точке и не пересекает дуги \(\omega_1\) и \(\omega_2\) и отрезок \(A B\), то есть исходная система имеет одно решение.
Значит, исходная система имеет больше двух решений при \(-2<a \leq-1\).
Ответ
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых уравнение
\begin{equation*}
\sqrt{3-5 x} \cdot \ln \left(4 x^2-a^2\right)=\sqrt{3-5 x} \cdot \ln (2 x+a)
\end{equation*}
имеет ровно один корень.
Решение
Исходное уравнение равносильно уравнению
\(\sqrt{3-5 x} \cdot\left(\ln \left(4 x^2-a^2\right)-\ln (2 x+a)\right)=0\).
Рассмотрим два случая.
Первый случай:
\(\sqrt{3-5 x}=0 \text { при условиях }\left\{\begin{array}{l}
4 x^2-a^2>0, \\
2 x+a>0
\end{array}\right.\)
Получаем \(x=\dfrac{3}{5}\). Условия принимают вид:
\(\left\{\begin{array} { l }
{ \dfrac { 3 6 } { 2 5 } - a ^ { 2 } > 0 , } \\
{ \dfrac { 6 } { 5 } + a > 0 ; }
\end{array} \left\{\begin{array}{l}
\dfrac{6}{5}-a>0 \\
\dfrac{6}{5}+a>0
\end{array}\right.\right.\)
откуда \(-\dfrac{6}{5}<a<\dfrac{6}{5}\). То есть в этом случае \(x=\dfrac{3}{5}\) при \(-\dfrac{6}{5}<a<\dfrac{6}{5}\).
Второй случай:
\(\ln \left(4 x^2-a^2\right)-\ln (2 x+a)=0\)
\(\text { при условии }3-5 x \geq 0\).
Получаем: \(\ln \left(4 x^2-a^2\right)=\ln (2 x+a) ;\)
\(\left\{\begin{array} { l }
{ ( 2 x - a ) ( 2 x + a ) = 2 x + a , } \\
{ 2 x + a > 0 ; }
\end{array} \left\{\begin{array}{l}
2 x-a=1, \\
2 x+a>0,
\end{array}\right.\right.\)
откуда \(x=\dfrac{a+1}{2}, a>-\dfrac{1}{2}\).
Условие \(3-5 x \geq 0\) принимает вид \(3-\dfrac{5 a+5}{2} \geq 0\) откуда \(a \leq \dfrac{1}{5}\).
То есть в этом случае \(x=\dfrac{a+1}{2}\) при \(-\dfrac{1}{2}<a \leq \dfrac{1}{5}\).
Корни уравнения \(x=\dfrac{3}{5}\) и \(x=\dfrac{a+1}{2}\) совпадают при \(a=\dfrac{1}{5}\).
Таким образом, исходное уравнение имеет ровно один корень при \(-\dfrac{6}{5}<a \leq-\dfrac{1}{2}\) и \(\dfrac{1}{5} \leq a<\dfrac{6}{5}\).
Ответ
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых система уравнений
\begin{equation*}
\left\{\begin{array}{l}
\left(x^2-7 x-y+8\right) \cdot \sqrt{x-y+8}=0, \\
y=a x+a
\end{array}\right.
\end{equation*}
имеет ровно два различных решения.
Решение
Каждое решение уравнения \(\left(x^2-7 x-y+8\right) \cdot \sqrt{x-y+8}=0\) либо является решением уравнения \(x-y+8=0\), откуда \(y=x+8\), либо является решением системы:
\begin{cases}
{x^2-7 x-y+8=0} \\
{x-y+8 \geq 0}
\end{cases}
\begin{cases} {y=x^2-7 x+8} \\
{y \leq x+8}
\end{cases}
\begin{cases} { y = x ^ { 2 } - 7 x + 8 , } \\
{ x ^ { 2 } - 7 x + 8 \leq x + 8 ; }
\end{cases}
\begin{cases} {y=x^2-7 x+8,} \\
{x^2-8 x \leq 0,}
\end{cases}
откуда \(y=x^2-7 x+8\) при условии \(0 \leq x \leq 8\).
Для каждого из этих случаев подставим \(y=a x+a\) и найдём количество корней получившегося уравнения в зависимости от \(a\).
Первый случай: \(a x+a=x+8\), откуда при \(a \neq 1\) получаем: \(x=\dfrac{8-a}{a-1}\).
При \(a=1\) корней нет.
Второй случай: \(a x+a=x^2-7 x+8\) при условии \(0 \leq x \leq 8\). Получаем квадратное уравнение \(x^2-(a+7) x-a+8=0\). Дискриминант этого уравнения равен \((a+7)^2+4(a-8)=a^2+18 a+17=\)
\((a+1)(a+17)\).
Значит, уравнение \(x^2-(a+7) x-a+8=0\) имеет два корня при \(a<-17\) и при \(a>-1\), имеет единственный корень \(x=\dfrac{a+7}{2}\) при \(a=-17\) и при \(a=-1\) и не имеет корней при \(-17<a<-1\).
При \(a<-17\) все коэффициенты уравнения \(x^2-(a+7) x-a+8=0\) положительны, а значит, его корни не удовлетворяют условию \(0 \leq x \leq 8\).
При \(a=-17\) корень уравнения \(x=-5\) не удовлетворяет условию \(0 \leq x \leq 8\), при \(a=-1\) корень уравнения \(x=3\) удовлетворяет условию \(0 \leq x \leq 8\).
При \(a>-1\) функция \(f(x)=x^2-(a+7) x-a+8\) принимает наименьшее значение при \(x=\dfrac{a+7}{2}\), и это значение отрицательно. Следовательно, больший корень уравнения \(f(x)=0\) удовлетворяет условию \(0 \leq x \leq 8\) тогда и только тогда, когда \(\dfrac{a+7}{2}<8\) и \(f(8) \geq 0 ; 16-9 a \geq 0\), откуда \(a \leq \dfrac{16}{9}\).
Меньший корень уравнения \(f(x)=0\) удовлетворяет условию \(x \geq 0\) тогда и только тогда, когда \(f(0) \geq 0 ;-a+8 \geq 0\), откуда \(a \leq 8\). В этом случае \(\dfrac{a+7}{2}<8\), а значит, этот корень удовлетворяет условию \(x \leq 8\).
Число \(\dfrac{8-a}{a-1}\) является корнем квадратного уравнения \(f(x)=0\) при \(\left(\dfrac{8-a}{a-1}\right)^2-(a+7)\left(\dfrac{8-a}{a-1}\right)-a+8=0\), откуда:
\((a-8)^2+(a+7)(a-8)(a-1)-\)
\((a-8)(a-1)^2=0 ;\)
\((a-8)^2+8(a-8)(a-1)=0 ;\)
\((a-8)(9 a-16)=0,\)
то есть при \(a=8\) и при \(a=\cfrac{16}{9}\).
Таким образом, исходная система уравнений имеет ровно два различных решения при \(a=-1 ; a=1 ; \dfrac{16}{9} \leq a<8\).
Ответ
(ЕГЭ, 2023) Найдите все значения \(a\), при каждом из которых система уравнений
\begin{equation*}
\left\{\begin{array}{l}
(x y-2 x+16) \cdot \sqrt{y-2 x+16}=0, \\
y=a x-14
\end{array}\right.
\end{equation*}
имеет ровно два различных решения.
Решение
Каждое решение уравнения \((x y-2 x+16) \cdot \sqrt{y-2 x+16}=0\) либо является решением уравнения \(y-2 x+16=0\), откуда \(y=2 x-16\), либо является решением системы:
\begin{cases}
{ x y - 2 x + 1 6 = 0 } \\
{ y - 2 x + 1 6 \geq 0 ; }
\end{cases}
\begin{cases}
{ y = \dfrac { 2 x - 1 6 } { x } , } \\
{ y - 2 x + 1 6 \geq 0 } \end{cases}
\begin{cases}
{ y = \dfrac { 2 x - 1 6 } { x } , } \\
{ \dfrac { 2 x - 1 6 } { x } - 2 x + 1 6 \geq 0 ; } \end{cases}
\begin{cases}
{y=\dfrac{2 x-16}{x},} \\
{(2 x-16) \cdot \dfrac{1-x}{x} \geq 0,} \end{cases}
откуда \(y=\dfrac{2 x-16}{x}\) при условии \(x<0\) или \(1 \leq x \leq 8\).
Для каждого из этих случаев подставим \(y=\alpha x-14\) и найдём количество корней получившегося уравнения в зависимости от \(a\).
Первый случай: \(a x-14=2 x-16\), откуда при \(a \neq 2\) получаем: \(x=-\dfrac{2}{a-2}\).
При \(a=2\) корней нет.
Второй случай: \(a x-14=\dfrac{2 x-16}{x}\) при условии \(x<0 ; 1 \leq x \leq 8\). Получаем уравнение \(a x^2-16 x+16=0\).
При \(a=0\) это уравнение имеет единственный корень \(x=1\).
При \(a \neq 0\) это уравнение квадратное, его дискриминант равен \(256-64 a=-64(a-4)\). Значит, уравнение \(a x^2-16 x+16=0\) имеет два корня при \(a<0\) и при \(0<a<4\), имеет единственный корень \(x=2\) при \(a=4\) и не имеет корней при \(a>4\).
При \(a<0\) функция \(f(x)=a x^2-16 x+16\) принимает наибольшее значение при \(x=\dfrac{8}{a}\), и это значение положительно.
Следовательно, меньший корень уравнения \(f(x)=0\) отрицателен, поскольку \(f(0)=16>0\). Этот корень удовлетворяет условию \(x<0\). Больший корень уравнения \(f(x)=0\) лежит в интервале \((0 ; 1)\), поскольку \(f(0)=16>0\), \(f(1)=a<0\). Следовательно, этот корень не удовлетворяет ни одному из условий \(x<0,1 \leq x \leq 8\).
При \(0<a<4\) корни уравнения \(f(x)=0\) положительны.
Функция \(f(x)=a x^2-16 x+16\) принимает наименьшее значение при \(x=\dfrac{8}{a}\), и это значение отрицательно. Следовательно, больший корень уравнения \(f(x)=0\) удовлетворяет условию \(1 \leq x \leq 8\) тогда и только тогда, когда \(\dfrac{8}{a}<8\) и \(f(8) \geq 0\); \(64 a-112 \geq 0\), откуда \(a \geq \dfrac{7}{4}\).
При \(0<a<4\) меньший корень уравнения лежит в интервале \((1 ; 2)\), поскольку \(f(1)=a>0, f(2)=4 a-16<0.\) Следовательно, этот корень удовлетворяет условию \(1 \leq x \leq 8\).
Число \(-\dfrac{2}{a-2}\) является корнем уравнения \(f(x)=0\) при \(a\left(\dfrac{2}{a-2}\right)^2+16 \cdot \dfrac{2}{a-2}+16=0\), откуда:
\(\dfrac{4 a+32(a-2)+16(a-2)^2}{(a-2)^2}=0 ; \)
\(\dfrac{16 a^2-28 a}{(a-2)^2}=0,\)
то есть при \(a=0\) и при \(a=\dfrac{7}{4}\).
Таким образом, исходная система уравнений имеет ровно два различных решения при \(a<0 ; 0<a \leq \dfrac{7}{4} ; a=2 ; a=4\).
