13. Тригонометрические, логарифмические, показательные и смешанные уравнения

142

(ЕГЭ,2019) а) Решите уравнение \(\sin 2 x=\sin x-2 \cos x+1\).

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[\frac{3 \pi}{2} ; 3 \pi\right]\).

a) \(-\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{3 \pi}{2} ; \frac{5 \pi}{3} ; \frac{7 \pi}{3}\).

a) \(\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z} ; \frac{\pi}{6}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{6}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{11 \pi}{6} ; \frac{13 \pi}{6} ; \frac{5 \pi}{2}\).

a) \(\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\); \(\frac{3\pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{9 \pi}{4} ; \frac{11 \pi}{4}\).

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \( 2\pi ; \frac{7 \pi}{3} ; \frac{8 \pi}{3} ; 3\pi\).

Решение

a) Запишем исходное уравнение в виде:

\(2 \sin x \cdot \cos x-\sin x+2 \cos x-1=0 ;(\sin x+1)(2 \cos x-1)=0\)

Значит, или \(\sin x=-1\), откуда \(x=-\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z}\), или \(\cos x=\frac{1}{2}\), откуда \(x=\frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\), или \(x=-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\)

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[\frac{3 \pi}{2} ; 3 \pi\right]\).

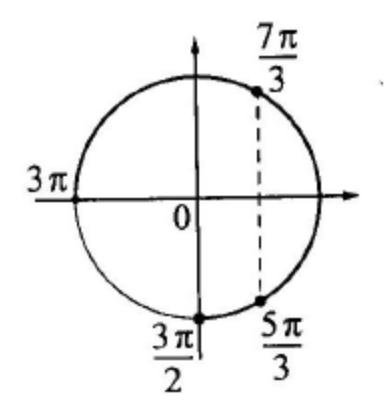
Получим числа: \(\frac{3 \pi}{2} ; \frac{5 \pi}{3} ; \frac{7 \pi}{3}\).

Ответ

a) \(-\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{3 \pi}{2} ; \frac{5 \pi}{3} ; \frac{7 \pi}{3}\).

143

(ЕГЭ,2019) а) Решите уравнение \(9^{\cos x}+9^{-\cos x}=\frac{10}{3}\).

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[2 \pi ; \frac{7 \pi}{2}\right]\).

а) \(\frac{\pi}{3}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2 \pi}{3}+2 \pi m, m \in \mathbb{Z} ;-\frac{2 \pi}{3}+2 \pi l, l \in \mathbb{Z}\); б) \(\frac{7 \pi}{3} ; \frac{8 \pi}{3} ; \frac{10 \pi}{3}\).

а) \(\frac{\pi}{6}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{6}+2 \pi n, n \in \mathbb{Z}\); \(\frac{5 \pi}{6}+2 \pi m, m \in \mathbb{Z} ;-\frac{5 \pi}{6}+2 \pi l, l \in \mathbb{Z}\); б) \(\frac{13 \pi}{6} ; \frac{17 \pi}{6} ; \frac{19 \pi}{6}\).

а) \(\frac{\pi}{10}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{10}+2 \pi n, n \in \mathbb{Z}\); \(\frac{7 \pi}{10}+2 \pi m, m \in \mathbb{Z} ;-\frac{7 \pi}{10}+2 \pi l, l \in \mathbb{Z}\); б) \(\frac{21 \pi}{10} ; \frac{27 \pi}{10} ; \frac{33 \pi}{10}\).

а) \(\frac{\pi}{4}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\); \(\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{9 \pi}{4} ; \frac{11 \pi}{4}\).

Решение

a) Пусть \(t=9^{\cos x}\), тогда исходное уравнение запишется в виде \(t+\frac{1}{t}=\frac{10}{3}\), откуда \(t=3\) или \(t=\frac{1}{3}\)

При \(t=3\) получим: \(9^{\cos x}=3\), откуда \(\cos x=\frac{1}{2} ; x=\frac{\pi}{3}+2 \pi k, k \in \mathbb{Z}\), или \(x=-\frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\)

При \(t=\frac{1}{3}\) получим: \(9^{\cos \mathrm{x}}=\frac{1}{3}\), откуда \(\cos x=-\frac{1}{2} ; x=\frac{2 \pi}{3}+2 \pi m, m \in \mathbb{Z}\), или \(x=-\frac{2 \pi}{3}+2 \pi l, l \in \mathbb{Z}\)

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[2 \pi ; \frac{7 \pi}{2}\right]\).

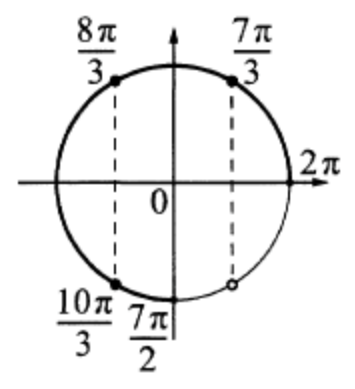
Получим числа: \(\frac{7 \pi}{3} ; \frac{8 \pi}{3} ; \frac{10 \pi}{3}\).

Ответ

а) \(\frac{\pi}{3}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2 \pi}{3}+2 \pi m, m \in \mathbb{Z} ;-\frac{2 \pi}{3}+2 \pi l, l \in \mathbb{Z}\); б) \(\frac{7 \pi}{3} ; \frac{8 \pi}{3} ; \frac{10 \pi}{3}\).

144

(ЕГЭ,2018) а) Решите уравнение \(\sqrt{x^3-5 x^2-9 x+22}=4-x\)

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-\frac{\sqrt{2}}{2} ; 2 \sqrt{10}\right]\).

Ответ

a) -1 ; 1; б) 1 .

145

(ЕГЭ,2018) а) Решите уравнение \(\sqrt{3} \sin x+2 \sin \left(2 x+\frac{\pi}{6}\right)=\sqrt{3} \sin 2 x+1\).

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-3 \pi ;-\frac{3 \pi}{2}\right]\).

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2 \pi}{3}+2 \pi m, m \in Z\); 6) \(-3 \pi ;-2 \pi ;-\frac{5 \pi}{3}\)

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{6}+2 \pi n, n \in \mathbb{Z}\); \(\frac{5 \pi}{6}+2 \pi m, m \in Z\); 6) \(-2 \pi ;-\frac{11 \pi}{6}\)

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{4}+ \pi n, n \in \mathbb{Z}\); \(\frac{3 \pi}{4}+ \pi m, m \in Z\); 6) \(-3 \pi ;-2 \pi ;-\frac{7 \pi}{4} ;-\frac{9 \pi}{4} ;-\frac{13 \pi}{4}\)

a) \(2\pi k, k \in \mathbb{Z} ; \frac{\pi}{2}+ \pi n, n \in \mathbb{Z}\); 6) \(-2 \pi ;-\frac{3 \pi}{2} ;-\frac{5 \pi}{2}\)

Ответ

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2 \pi}{3}+2 \pi m, m \in Z\); 6) \(-3 \pi ;-2 \pi ;-\frac{5 \pi}{3}\)

146

(ЕГЭ,2018) а) Решите уравнение \(2 \sin \left(2 x+\frac{\pi}{6}\right)-\cos x=\sqrt{3} \sin 2 x-1\)

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[\frac{5 \pi}{2} ; 4 \pi\right]\).

a) \(\frac{\pi}{2}+\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{5 \pi}{2} ; \frac{7 \pi}{2} ; \frac{11 \pi}{3}\).

a) \(\frac{\pi}{2}+2\pi k, k \in \mathbb{Z} ; \frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{5 \pi}{2} ; \frac{15 \pi}{4}\).

a) \(\frac{\pi}{2}+\pi k, k \in \mathbb{Z} ; \frac{\pi}{6}+ \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{5 \pi}{2} ; \frac{7 \pi}{2} ; \frac{19 \pi}{6}\).

a) \(-\frac{\pi}{2}+\pi k, k \in \mathbb{Z} ; -\frac{\pi}{3}+ \pi m, m \in \mathbb{Z}\); б) \(\frac{7 \pi}{2} ; \frac{8 \pi}{3} ; \frac{11 \pi}{3}\).

Ответ

a) \(\frac{\pi}{2}+\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{\pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{5 \pi}{2} ; \frac{7 \pi}{2} ; \frac{11 \pi}{3}\).

147

(ЕГЭ,2018) а) Решите уравнение \(2 \sqrt{2} \sin \left(x+\frac{\pi}{3}\right)+2 \cos ^2 x=\sqrt{6} \cos x+2\).

б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-3 \pi ;-\frac{3 \pi}{2}\right]\).

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\); \(\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(-3 \pi ;-2 \pi ;-\frac{7 \pi}{4}\).

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{3}+2 \pi n, n \in \mathbb{Z}\); \(\frac{2 \pi}{3}+2 \pi m, m \in \mathbb{Z}\); б) \(-3 \pi ;-2 \pi ;-\frac{5 \pi}{3}\).

a) \(\pi + \pi k, k \in \mathbb{Z} ; \frac{\pi}{6}+ \pi n, n \in \mathbb{Z}\); \(\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(-3 \pi ;-\frac{11 \pi}{6} ;-\frac{17 \pi}{6}\).

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{2}+ \pi n, n \in \mathbb{Z}\); б) \(-3 \pi ;-2 \pi ;-\frac{3 \pi}{2} ;-\frac{5 \pi}{2}\).

Ответ

a) \(\pi k, k \in \mathbb{Z} ; \frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\); \(\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(-3 \pi ;-2 \pi ;-\frac{7 \pi}{4}\).