a) Пусть \(t=\frac{1}{\sin x}\), тогда уравнение запишется в виде \(t^2+t-2=0\), откуда \(t=1\) или \(t=-2\).

При \(t=1\) получим: \(\frac{1}{\sin x}=1 ; \sin x=1\), откуда \(x=\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z}\).

При \(t=-2\) получим: \(\frac{1}{\sin x}=-2 ; \sin x=-\frac{1}{2}\), откуда \(x=-\frac{\pi}{6}+2 \pi n, n \in \mathbb{Z}\), или \(x=-\frac{5 \pi}{6}+2 \pi m, m \in \mathbb{Z}\).

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[\frac{3 \pi}{2} ; 3 \pi\right]\).

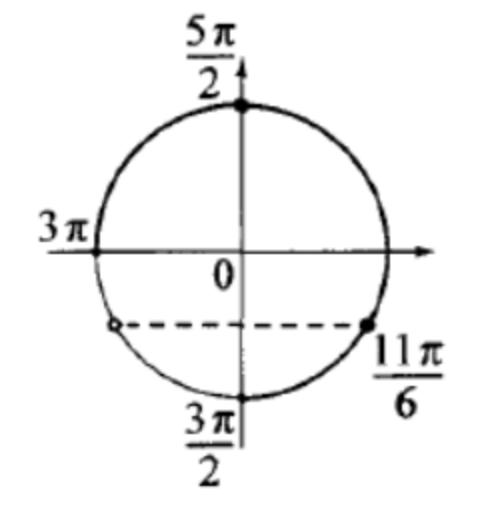
Получим числа: \(\frac{11 \pi}{6} ; \frac{5 \pi}{2}\).

а) \(\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z} ;-\frac{\pi}{6}+2 \pi n, n \in \mathbb{Z}\); \(-\frac{5 \pi}{6}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{11 \pi}{6} ; \frac{5 \pi}{2}\).

a) Пусть \(t=\log _4(4 \sin x)\), тогда исходное уравнение запишется в виде \(2 t^2-5 t+2=0\), откуда \(t=2\) или \(t=\frac{1}{2}\).

При \(t=2\) получим: \(\log _4(4 \sin x)=2\), значит, \(\sin x=4\), что невозможно.

При \(t=\frac{1}{2}\) получим: \(\log _4(4 \sin x)=\frac{1}{2}\), значит, \(\sin x=\frac{1}{2}\), откуда \(x=\frac{\pi}{6}+2 \pi n\), \(n \in \mathbb{Z}\), или \(x=\frac{5 \pi}{6}+2 \pi m, m \in \mathbb{Z}\).

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[-\frac{3 \pi}{2} ; 0\right]\).

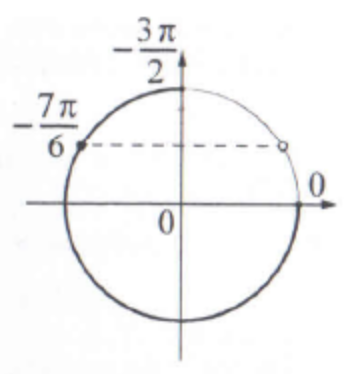
Получим число \(-\frac{7 \pi}{6}\).

а) \(\frac{\pi}{6}+2 \pi n, n \in \mathbb{Z} ; \frac{5 \pi}{6}+2 \pi m, m \in \mathbb{Z}\); б) \(-\frac{7 \pi}{6}\).

a) Запишем исходное уравнение в виде:
\(\log _5(2-x)=\log _5 x^2:\left\{\begin{array}{l}x^2=2-x, \\ x^2>0 ;\end{array}\left\{\begin{array}{l}(x+2)(x-1)=0, \\ x \neq 0 .\end{array}\right.\right.\)

Получаем, что \(x=-2\) или \(x=1\).

б) Поскольку \(\log _9 \frac{1}{82}<-2<\log _9 8<1\), получаем, что отрезку \(\left[\log _9 \frac{1}{82} ; \log _9 8\right]\) принадлежит единственный корень -2.

а) \(-2 ; 1 ;\) б) -2

a) Запишем исходное уравнение в виде: 

\(6-6 \sin ^2 x+5 \sqrt{2} \sin x+2=0 ;(2 \sin x+\sqrt{2})(3 \sin x-4 \sqrt{2})=0\)

Значит, \(\sin x=-\frac{\sqrt{2}}{2}\), откуда \(x=-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\), или \(x=-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\).

Уравнение \(\sin x=\frac{4 \sqrt{2}}{3}\) корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[\pi ; \frac{5 \pi}{2}\right]\).

Получим числа: \(\frac{5 \pi}{4} ; \frac{7 \pi}{4}\).
 

а) \(-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z} ;-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{5 \pi}{4} ; \frac{7 \pi}{4}\).

a) Запишем исходное уравнение в виде: 

\(2-2 \sin ^2 x+2 \sqrt{2} \sin x+1=0 ;(\sqrt{2} \sin x+1)(\sqrt{2} \sin x-3)=0\)

Значит, \(\sin x=-\frac{\sqrt{2}}{2}\), откуда \(x=-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\), или \(x=-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\)

Уравнение \(\sin x=\frac{3 \sqrt{2}}{2}\) корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[\frac{3 \pi}{2} ; 3 \pi\right]\).

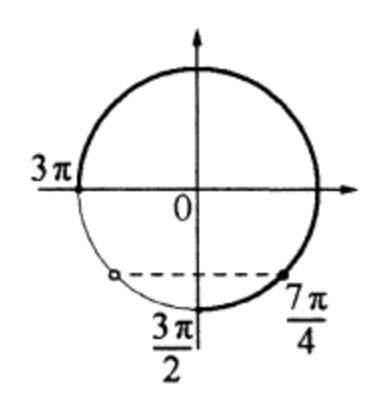
Получим число \(\frac{7 \pi}{4}\).

а) \(-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z} ;-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{7 \pi}{4}\).

a) Запишем исходное уравнение в виде: 

\(2 \sin ^2 x+3 \sqrt{2} \sin x+2=0 ;(2 \sin x+\sqrt{2})(\sin x+\sqrt{2})=0\)

Значит, \(\sin x=-\frac{\sqrt{2}}{2}\), откуда \(x=-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z}\), или \(x=-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\)

Уравнение \(\sin x=-\sqrt{2}\) корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку \(\left[\frac{5 \pi}{2} ; 4 \pi\right]\).

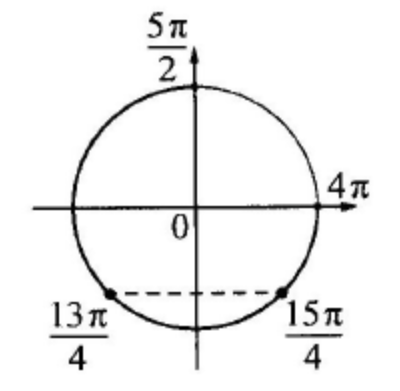
Получим числа: \(\frac{13 \pi}{4} ; \frac{15 \pi}{4}\).

Ответ: a) \(-\frac{\pi}{4}+2 \pi n, n \in \mathbb{Z} ;-\frac{3 \pi}{4}+2 \pi m, m \in \mathbb{Z}\); б) \(\frac{13 \pi}{4} ; \frac{15 \pi}{4}\).