a) Плоскость \(M N K\) пересекает плоскости оснований \(A B C D\) и \(A_1 B_1 C_1 D_1\) по параллельным прямым, значит, прямые \(N K\) и \(M L\) параллельны и \(C L=1\).

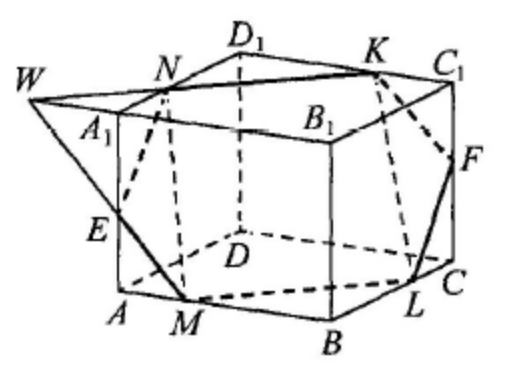
Вычислим стороны и диагонали четырёхугольника \(M N K L\) :
\begin{equation*}
\begin{gathered}
N K=M L=\sqrt{M B^2+B L^2}=5 \sqrt{2}, \\
L K=M N=\sqrt{M A^2+A A_1^2+A_1 N^2}=5 \sqrt{2},
\end{gathered}
\end{equation*}

\begin{equation*}
M K=\sqrt{\left(M B-K C_1\right)^2+B C^2+C C_1^2}=\sqrt{\left(B L-N A_1\right)^2+A B^2+A A_1^2}=L N .
\end{equation*}

Поэтому \(M N K L\) - квадрат.

б) Пусть \(W\) - точка пересечения прямых \(N K\) и \(A_1 B_1\). Torда \(W A_1=N A_1=M A\), поэтому прямая \(W M\), а значит и плоскость \(M N K\), пересекает ребро \(A A_1\) в его середине \(E\). Аналогично, плоскость \(M N K\) пересекает ребро \(C C_1\) в его середине \(F\).

В прямоугольнике \(A E F C\) имеем \(E F=A C=6 \sqrt{2}\). Сечение \(M E N K F L\) состоит из двух равных трапеций \(E N K F\) и \(E M L F\), причём прямая \(M N\) перпендикулярна их основаниям. Значит, искомая площадь равна
\begin{equation*}
2 \cdot \frac{M L+E F}{2} \cdot \frac{M N}{2}=55 \text {. }
\end{equation*}

a) Проведём через точки \(K\) и \(L\) прямые, параллельные \(A C\). Пусть эти прямые пересекают рёбра \(B C\) и \(A_1 B_1\) в точках \(K_1\) и \(L_1\) соответственно.

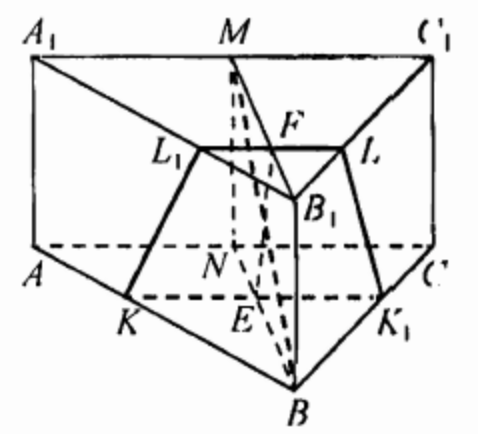
Тогда трапеция \(K L_1 L K_1\) является сечением исходной призмы плоскостью \(\gamma\). 

Рассмотрим плоскость \(B B_1 M\). Пусть эта плоскость пересекает прямые \(A C, K K_1\) и \(L L_1\) в точках \(N, E\) и \(F\) соответственно. Четырёхугольник \(B B_1 M N\) - прямоугольник, причём
\begin{equation*}
B B_1=3 \sqrt{6}, B_1 M=\frac{\sqrt{3}}{2} \cdot A_1 B_1=6 \sqrt{3} .
\end{equation*}

Кроме того, \(N E: E B=A K: K B=1: 5, \quad B_1 F: F M=B_1 L: L C_1=1: 2\), откуда \(M F=4 \sqrt{3}, N E=\sqrt{3}\).

Пусть \(F P\) - высота трапеции \(E F B_1 B\), тогда \(\begin{gathered}E P=M F-N E=3 \sqrt{3} . \\ \text { Поскольку } \operatorname{tg} \angle B E F=\frac{F P}{E P}=\sqrt{2}=\frac{M B_1}{B B_1}=\operatorname{tg} \angle M B B_1, \\ \angle B E F=\angle M B B_1=90^{\circ}-\angle M B E,\end{gathered}\) то есть прямые \(E F\) и \(B M\) перпендикулярны.

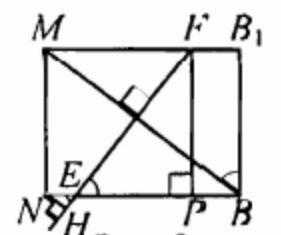
Прямая \(K K_1\) параллельна прямой \(A C\), которая перпендикулярна плоскости \(B B_1 M\). Значит, прямые \(K K_1\) и \(E F\) перпендикулярны прямой \(B M\), поэтому прямая \(B M\) перпендикулярна плоскости \(\gamma\).

б) Поскольку прямая \(A C\) параллельна плоскости \(\gamma\), расстояние от точки \(C\) до плоскости \(\gamma\) равно расстоянию от точки \(N\) до прямой \(E F\). Опустим из точки \(N\) перпендикуляр \(N H\) на прямую \(E F\). Тогда
\begin{equation*}
N H=N E \cdot \sin \angle N E H=N E \cdot \sin \angle B E F=\sqrt{3} \cdot \frac{\sqrt{2}}{\sqrt{3}}=\sqrt{2} .
\end{equation*}

a) Проведём через точки \(K\) и \(L\) прямые, параллельные \(B D\). Пусть эти прямые пересекают рёбра \(C D\) и \(B_1 C_1\) в точках \(K_1\) и \(L_1\) соответственно.

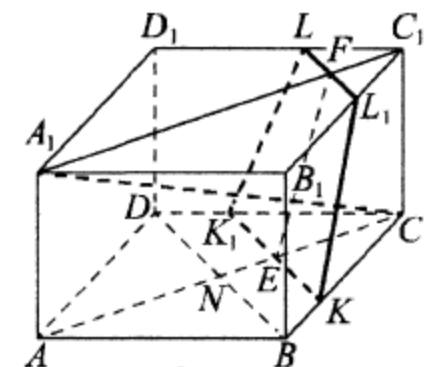
Тогда трапеция \(K L_1 L K_1\) является сечением исходной призмы плоскостью \(\gamma\). 

Рассмотрим плоскость \(A C C_1\). Пусть эта плоскость пересекает прямые \(K K_1\) и \(L L_1\) в точках \(E\) и \(F\) соответственно. Четырёхугольник \(A A_1 C_1 C\) - прямоугольник, причём
\begin{equation*}
A A_1=4 \sqrt{2}, A C=8 \sqrt{2} \text {. }
\end{equation*}

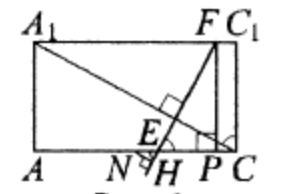
Кроме того, \(\frac{A C}{E C}=\frac{2 B C}{K C}=\frac{8}{3}, \frac{A_1 C_1}{F C_1}=\frac{2 D_1 C_1}{L C_1}=8\), откуда \(E C=3 \sqrt{2}, C_1 F=\sqrt{2}\).
Пусть \(F P\) - высота трапеции \(E F C_1 C\) (рис. 2), тогда \(E P=E C-C_1 F=2 \sqrt{2}\).

Поскольку \(\operatorname{tg} \angle C E F=\frac{F P}{E P}=2=\frac{A_1 C_1}{C C_1}=\operatorname{tg} \angle A_1 C C_1\),
\begin{equation*}
\angle C E F=\angle A_1 C C_1=90^{\circ}-\angle A_1 C A \text {, }
\end{equation*}

то есть прямые \(E F\) и \(A_1 C\) перпендикулярны.

Прямая \(K K_1\) параллельна прямой \(B D\), которая перпендикулярна плоскости \(A A_1 C\). Значит, прямые \(K K_1\) и \(E F\) перпендикулярны прямой \(A_1 C\), поэтому прямая \(A_1 C\) перпендикулярна плоскости \(\gamma\).

б) Пусть \(N\) - точка пересечения \(A C\) и \(B D\). Поскольку прямая \(B D\) параллельна плоскости \(\gamma\), расстояние от точки \(B\) до плоскости \(\gamma\) равно расстоянию от точки \(N\) до прямой \(E F\). Опустим из точки \(N\) перпендикуляр \(N H\) на прямую \(E F\). Тогда
\begin{equation*}
N H=N E \cdot \sin \angle N E H=\left(\frac{A C}{2}-E C\right) \cdot \sin \angle C E F=\sqrt{2} \cdot \frac{2}{\sqrt{5}}=\frac{2 \sqrt{10}}{5} .
\end{equation*}

a) Поскольку пирамида \(S A B C D\) правильная, точки \(T\) и \(H\) лежат в плоскости \(S N M\), перпендикулярной плоскости \(A B C\).

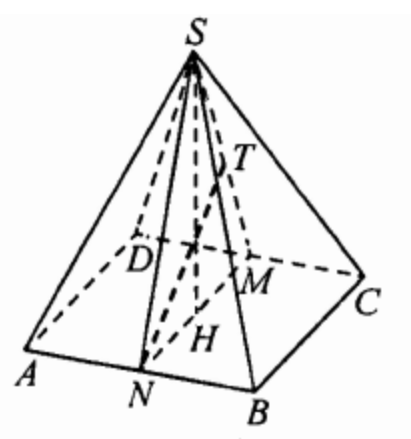
\begin{equation*}
\begin{gathered}
A H=\frac{A B}{\sqrt{2}}=\sqrt{6}, A S=\sqrt{S H^2+A H^2}=\sqrt{15}, \\
M N=A D=2 \sqrt{3}, S M=S N=\sqrt{S A^2-A N^2}=2 \sqrt{3} .
\end{gathered}
\end{equation*}

Значит, треугольник \(S N M\) равносторонний, а \(N T\) его высота. Следовательно, \(T\) - середина \(S M\).

б) Пусть E - основание перпендикуляра, опущенного из точки \(T\) на прямую \(S C\).

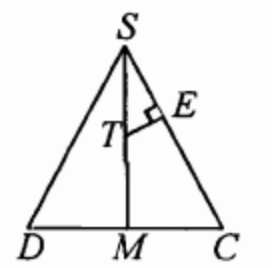
Прямые \(N T\) и \(T E\) перпендикулярны, так как \(N T\) - высота пирамиды \(N S C D\). Поскольку отрезок \(TE\) перпендикулярен как прямой \(S C\), так и прямой \(N T\), его длина и есть искомое расстояние. Прямоугольные треугольники \(S E T\) и \(S M C\) подобны, следовательно, \(\frac{E T}{M C}=\frac{S T}{S C}\), откуда \(E T=\frac{S T \cdot C M}{S C}=\frac{S M \cdot C D}{4 S C}=\frac{\sqrt{15}}{5}\).