a) Пусть плоскость \(\alpha\) пересекает прямые \(S B\) и \(A B\) в точках \(L\) и \(M\) соответственно.

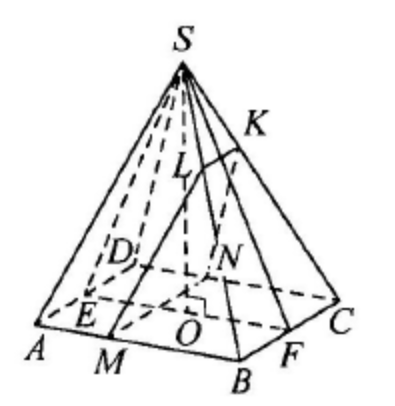
Поскольку плоскость \(\alpha\) параллельна прямой \(B C\), прямые \(K L\) и \(B C\) параллельны. Следовательно,
\begin{equation*}
S L: L B=S K: K C=1: 7 \text {. }
\end{equation*}

б) Поскольку отрезки \(B C\) и \(A D\) параллельны, а плоскость \(\alpha\) параллельна прямой \(B C\), прямые \(M N\) и \(A D\) параллельны. По условию \(D N: N C=S K: K C\), значит, прямые \(S D\) и \(K N\) параллельны. Следовательно, плоскость \(S A D\) параллельна плоскости \(\alpha\). Значит, расстояние между прямыми \(S A\) и \(K N\) равно расстоянию между плоскостями \(S A D\) и \(\alpha\).
Пусть точки \(E\) и \(F\) - середины рёбер \(A D\) и \(B C\) соответственно. Тогда прямые \(S E\) и \(E F\) перпепдикулярны прямой \(A D\). Таким образом, плоскость \(S E F\) перпендикулярна плоскости \(S A D\) и параллельной ей плоскости \(\alpha\).

Пусть плоскость \(S E F\) пересекает прямые \(K L\) и \(M N\) в точках \(Q\) и \(R\) соответственно.

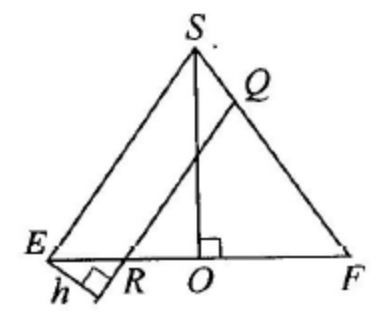
Тогда искомое расстояние равно расстоянию \(h\) между прямыми \(S E\) и \(Q R\). Высота \(S O\) пирамиды \(S A B C D\) лежит в плоскости \(S E F\), откуда
\begin{equation*}
\begin{gathered}
E F=8, S E=\sqrt{S A^2-\frac{A D^2}{4}}=2 \sqrt{21} ; \cos \angle S E O=\frac{E F}{2 S E}=\frac{2}{\sqrt{21}} ; \\
h=E R \cdot \sin \angle S E O=\frac{E F}{8} \cdot \sqrt{1-\frac{4}{21}}=\frac{\sqrt{357}}{21} .
\end{gathered}
\end{equation*}

a) Пусть плоскость \(A M B\) пересекает прямую \(B_1 C_1\)
в точке \(N\). Тогда сечение призмы \(A B C A_1 B_1 C_1\)
плоскостью \(A M B\) - четырёхугольник \(A M N B\).

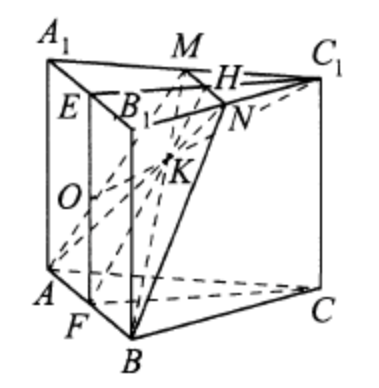
Плоскость \(A M B\) пересекает плоскости \(A B_1 C_1\)
и \(B A_1 C_1\) по прямым \(A N\) и \(M B\) соответственно,
а плоскости \(A B_1 C_1\) и \(B A_1 C_1\) пересекаются
по прямой \(O C_1\). Значит, точка пересечения
плоскостей \(A M B, A B_1 C_1\) и \(B A_1 C_1\) принадлежит каждой из прямых \(A N, M B\) и \(O C_1\), то есть точка пересечения диагоналей четырёхугольника \(A M N B\) лежит на отрезке \(O C_1\).

б) Пусть прямые \(A N, M B\) и \(O C_1\) пересекаются в точке \(K\), а плоскость \(C O C_1\) пересекает прямые \(A B, A_1 B_1\) и \(M N\) в точках \(F, E\) и \(H\) соответственно. 

Поскольку \(O\) - точка пересечения диагоналей прямоугольника \(A B B_1 A_1\), точки \(F\) и \(E\) являются серединами отрезков \(A B\) и \(A_1 B_1\) соответственно. Следовательно, прямые \(O F\) и \(C F\) перпендикулярны прямой \(A B\). Значит, плоскость \(C_1\) перпендикулярна прямой \(A B\) и содержащей её плоскости \(A M B\). Таким образом, искомый угол равен углу \(C_1 K H\).

Прямые \(A_1 B_1\) и \(M N\) параллельны, следовательно, \(M N-\) средняя линия треугольника \(A_1 B_1 C_1\), а значит, точка \(H\) - середина отрезка \(E C_1\).
В треугольнике \(E F C_1\) медианы пересекаются в точке \(K\). Имеем:
\begin{equation*}
\begin{aligned}
& C_1 H=\frac{\sqrt{3}}{2}, C_1 K= \frac{2}{3} \sqrt{\frac{E F^2}{4}+C_1 E^2}=\frac{4 \sqrt{3}}{3}, K H=\frac{1}{3} \sqrt{E F^2+\frac{C_1 E^2}{4}}=\frac{7 \sqrt{3}}{6} ; \\
& \cos \angle H K C_1=\frac{K H^2+C_1 K^2-C_1 H^2}{2 \cdot K H \cdot C_1 K}=\frac{13}{14} .
\end{aligned}
\end{equation*}