a) Пусть точки \(H\) и \(H_1\) - середины ребер \(A B\) и \(A_1 B_1\) соответственно.

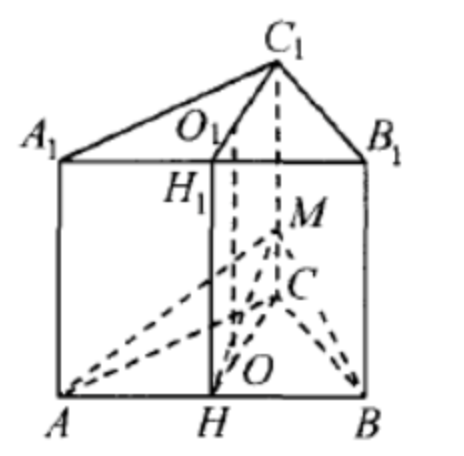
Треугольники \(A B C\) и \(A_1 B_1 C_1\) правильные, поэтому точки \(O\) и \(O_1\) лежат в плоскости \(C H C_1\) и \(O H: O C=O_1 H_1: O_1 C_1=1: 2\).
Рассмотрим плоскость \(\mathrm{CHC}_1\). Пусть отрезки \(O O_1\) и \(H M\) пересекаются в точке \(E\) .

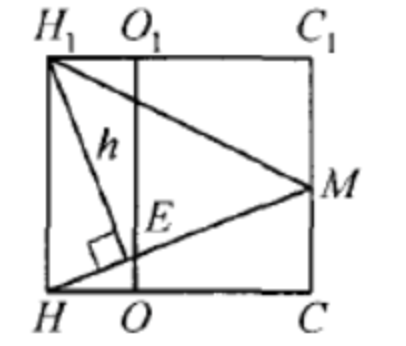
По теореме Фалеса
\begin{equation*}
H E: E M=H O: O C=1: 2 .
\end{equation*}

Точка пересечения медиан треугольника \(A B M\) лежит на отрезке \(M H\) и делит его в отношении \(2: 1\), считая от вершины \(M\), то есть совпадает с точкой \(E\). Значит, прямая \(O O_1\) содержит точку пересечения медиан треугольника \(A B M\).

б) Поскольку прямые \(A B\) и \(A_1 B_1\) параллельны, прямая \(A_1 B_1\) параллельна плоскости \(A B M\). Значит, искомое расстояние равно расстоянию \(h\) от точки \(H_1\) до плоскости \(A M B\).

Прямая \(A B\) перпендикулярна прямым \(C H\) и \(C C_1\), Значит, прямая \(A B\) и содержащая её плоскость \(A M B\) перпендикулярны плоскости \(C H C_1\), а искомое расстояние равно высоте треугольника \(H M H_1\), проведённой к стороне \(H M\).
Площадь треугольника \(H M H_1\) равна \(\frac{H H_1 \cdot C H}{2}=\frac{A A_1 \cdot A B \cdot \sqrt{3}}{4}=14 \sqrt{3}\).
С другой стороны, его площадь равна \(\frac{h \cdot H M}{2}=\frac{h \cdot \sqrt{\frac{3 A B^2}{4}+C M^2}}{2}=\frac{7 h}{2}\), откуда \(h=4 \sqrt{3}\).

a) Пусть точка \(H\) - середина ребра \(B C\). Тогда медианы \(A H\) и \(SH\) равнобедренных треугольников \(A B C\) и \(S B C\) соответственно являются их высотами, а значит, плоскость ASH перпендикулярна прямой \(B C\). Следовательно, прямая \(S A\) перпендикулярна прямой \(B C\).

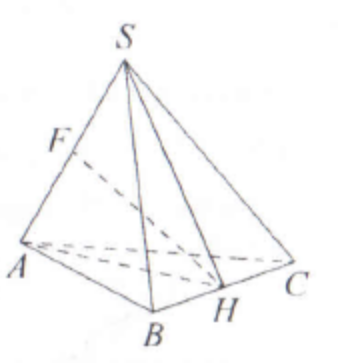
б) Пусть точка \(F\) - середина ребра \(S A\). Тогда, поскольку \(A H=S H\), медиана \(H F\) треугольника \(A H S\) перпендикулярна прямой \(S A\).

Плоскость \(A S H\) перпендикулярна прямой \(B C\), следовательно, прямая \(F H\) перпендикулярна прямой \(B C\). Таким образом, расстояние между прямыми \(S A\) и \(B C\) равно длине отрезка \(F H\).
В треугольнике \(A S H\) :
\begin{equation*}
F S=\sqrt{7}, S H=\sqrt{S B^2-\frac{B C^2}{4}}=2 \sqrt{6},
\end{equation*}

откуда \(F H=\sqrt{S H^2-F S^2}=\sqrt{17}\).

a) Поскольку точка \(M\) - середина образующей \(S A\), а прямая \(M N\) параллельна образующей \(S B\), точка \(N\) - середина отрезка \(A B\).

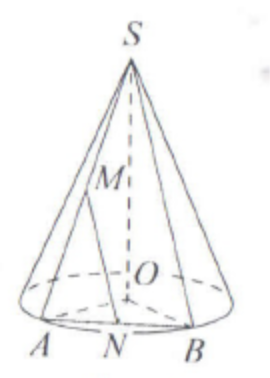
Медиана \(NO\) равнобедренного треугольника \(A O B\) является его высотой. Таким образом, \(\angle A N O=90^{\circ}\).

б) Пусть точка \(H\) - середина отрезка \(A O\) .

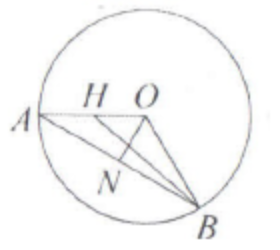
Средняя линия \(M H\) треугольника \(A S O\) параллельна высоте конуса \(S O\), а значит, прямая \(MH\) перпендикулярна плоскости основания конуса. Следовательно, угол между прямой \(B M\) и плоскостью основания конуса равен углу \(M B H\).
В треугольнике \(A O B\) :
\begin{equation*}
\begin{gathered}
\cos \angle O A B=\frac{A N}{A O}=0,8 ; \\
B H=\sqrt{A H^2+A B^2-2 A H \cdot A B \cdot \cos \angle O A B}=\frac{\sqrt{153}}{2} .
\end{gathered}
\end{equation*}

В треугольнике \(M H B\) :
\begin{equation*}
M H=\frac{\sqrt{51}}{2} ; \operatorname{tg} \angle M B H=\frac{M H}{H B}=\frac{\sqrt{3}}{3},
\end{equation*}

откуда \(\angle M B H=30^{\circ}\).

a) Пусть точка \(H\) - середина ребра \(B C\), а плоскость \(\alpha\) пересекает рёбра \(S B\) и \(A C\) в точках \(L\) и \(N\) соответственно.

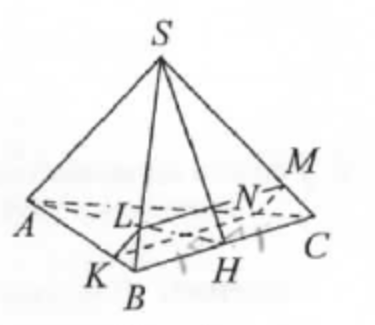
Тогда медианы \(A H\) и \(S H\) треугольников \(A B C\) и \(S B C\) соответственно являются их высотами, а значит, плоскость \(A S H\) перпендикулярна прямой \(B C\). Следовательно, прямая \(S A\) перпендикулярна прямой \(B C\).
Поскольку прямая \(S A\) параллельна плоскости \(\alpha\), прямые \(K L\) и \(M N\) параллельны прямой \(S A\), а значит,
\begin{equation*}
S L: L B=A K: K B=S M: M C=A N: N C .
\end{equation*}

Следовательно, прямые \(L M\) и \(K N\) параллельны прямой \(B C\).
Таким образом, \(KLMN\) является параллелограммом, пары противоположных сторон которого параллельны перпендикулярным прямым \(S A\) и \(B C\) соответственно, то есть \(K L M N\) - прямоугольник.

б) Прямая \(B C\), параллельная прямой \(K N\), перпендикулярна плоскости \(A S H\), значит, плоскости \(A S H\) и \(\alpha\) перпендикулярны.

Пусть плоскость \(A S H\) пересекает прямые \(K N\) и \(L M\) в точках \(E\) и \(F\) соответственно.

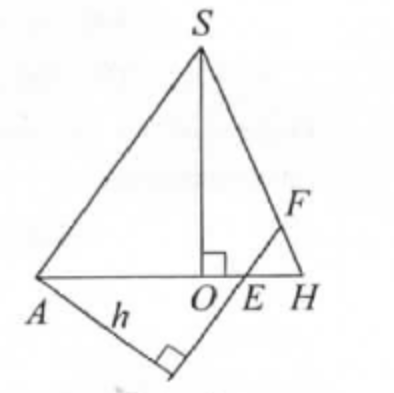
Тогда высота пирамиды \(A K L M N\) равна расстоянию \(h\) между прямыми \(S A\) и \(E F\).
Высота \(S O\) пирамиды \(S A B C\) лежит в плоскости \(A S H, A O: O H=2: 1\), откуда
\begin{equation*}
\begin{aligned}
& A H=3 \sqrt{3} ; A O=\frac{2 A H}{3}=2 \sqrt{3} ; \cos \angle S A O=\frac{A O}{S A}=\frac{2 \sqrt{3}}{5} ; \\
& h=A E \sin \angle S A O=\frac{5 A H}{6} \cdot \sqrt{1-\frac{12}{25}}=\frac{5 \sqrt{3}}{2} \cdot \sqrt{\frac{13}{25}}=\frac{\sqrt{39}}{2} .
\end{aligned}
\end{equation*}

Объём пирамиды \(A K L M N\) равен
\begin{equation*}
K N \cdot K L \cdot \frac{h}{3}=\frac{5 B C}{6} \cdot \frac{S A}{6} \cdot \frac{\sqrt{39}}{6}=5 \cdot \frac{5}{6} \cdot \frac{\sqrt{39}}{6}=\frac{25 \sqrt{39}}{36} .
\end{equation*}

a) Пусть плоскость \(\alpha\) пересекает ребро \(S B\) в точке \(L\). Поскольку прямая \(B C\) параллельна плоскости \(\alpha\), прямые \(L M\) и \(B C\) параллельны, а значит,
\begin{equation*}
S L: L B=S M: M C=A K: K B \text {. }
\end{equation*}

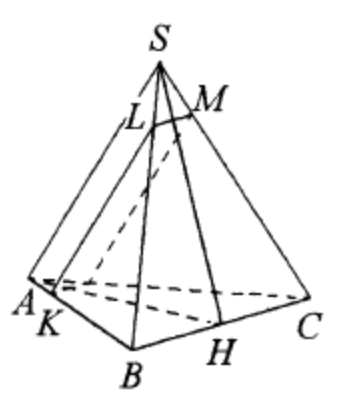
Следовательно, прямые \(K L\) и \(S A\) параллельны. Таким образом, плоскость \(\alpha\), содержащая прямую \(K L\), параллельна прямой \(S A\).

б) Пусть точка \(H\) - середина ребра \(B C\). Тогда медианы \(A H\) и \(S H\) треугольников \(A B C\) и \(S B C\) соответственно являются их высотами, а значит, плоскость \(A S H\) перпендикулярна прямой \(B C\).

Следовательно, плоскость \(A S H\) перпендикулярна плоскости \(\alpha\), параллельной прямой \(B C\), и плоскости \(S B C\), содержащей прямую \(B C\).
Поскольку плоскость \(\alpha\) параллельна прямой \(S A\), лежащей в плоскости \(A S H\), искомый угол равен углу между прямой \(S A\) и плоскостью \(S B C\).
Таким образом, угол между плоскостями \(\alpha\) и \(S B C\) равен углу \(A S H\). В треугольнике \(A S H\) имеем:
\begin{equation*}
A S=7, A H=3 \sqrt{3}, S H=\sqrt{S B^2-B H^2}=\sqrt{S B^2-\frac{B C^2}{4}}=2 \sqrt{10} .
\end{equation*}

По теореме косинусов
\begin{equation*}
\cos \angle A S H=\frac{S A^2+S H^2-A H^2}{2 S A \cdot S H}=\frac{49+40-27}{2 \cdot 7 \cdot 2 \sqrt{10}}=\frac{31 \sqrt{10}}{140} .
\end{equation*}

a) Пусть плоскость \(\alpha\) пересекает рёбра \(S B\) и \(A C\) в точках \(L\) и \(N\) соответственно.

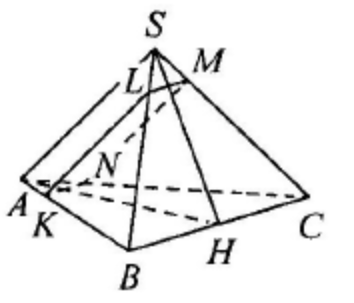
Поскольку прямая \(S A\) параллельна плоскости \(\alpha\), прямые \(M N\) и \(S A\) параллельны, а значит,
\begin{equation*}
A N: N C=S M: M C=1: 4 \text {. }
\end{equation*}

б) Пусть точка \(H\) - середина ребра \(B C\). Тогда медианы \(A H\) и \(S H\) треугольников \(A B C\) и \(S B C\) соответственно являются их высотами, а значит, плоскость \(A S H\) перпендикулярна прямой \(B C\).
Поскольку плоскость \(\alpha\) параллельна прямой \(S A\), расстояние между прямыми \(S A\) и \(K M\) равно расстоянию между прямой \(S A\) и плоскостью \(\alpha\). Прямые \(B C\) и \(K N\) параллельны, поскольку
\begin{equation*}
A N: N C=A K: K B=1: 4 .
\end{equation*}

Пусть плоскость \(A S H\) пересекает прямые \(K N\) и \(L M\) в точках \(E\) и \(F\) соответственно.

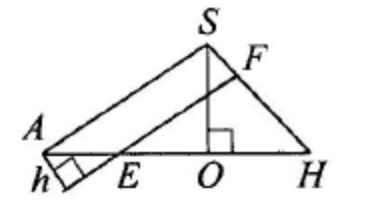
Тогда расстояние между прямой \(S A\) и плоскостью \(\alpha\) равно расстоянию \(h\) между прямыми \(S A\) и \(E F\).
Высота \(S O\) пирамиды \(S A B C\) лежит в плоскости \(A S H, A O: O H=2: 1\), откуда
\begin{equation*}
\begin{aligned}
A H & =\frac{5 \sqrt{3}}{2} ; A O=\frac{2 A H}{3}=\frac{5 \sqrt{3}}{3} ; \cos \angle S A O=\frac{A O}{S A}=\frac{5 \sqrt{3}}{9} ; \\
h & =A E \cdot \sin \angle S A O=\frac{A H}{5} \cdot \sqrt{1-\frac{75}{81}}=\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{6}}{9}=\frac{\sqrt{2}}{6} .
\end{aligned}
\end{equation*}