14. Стереометрия
Чтобы получить дополнительный функционал нужно войти.
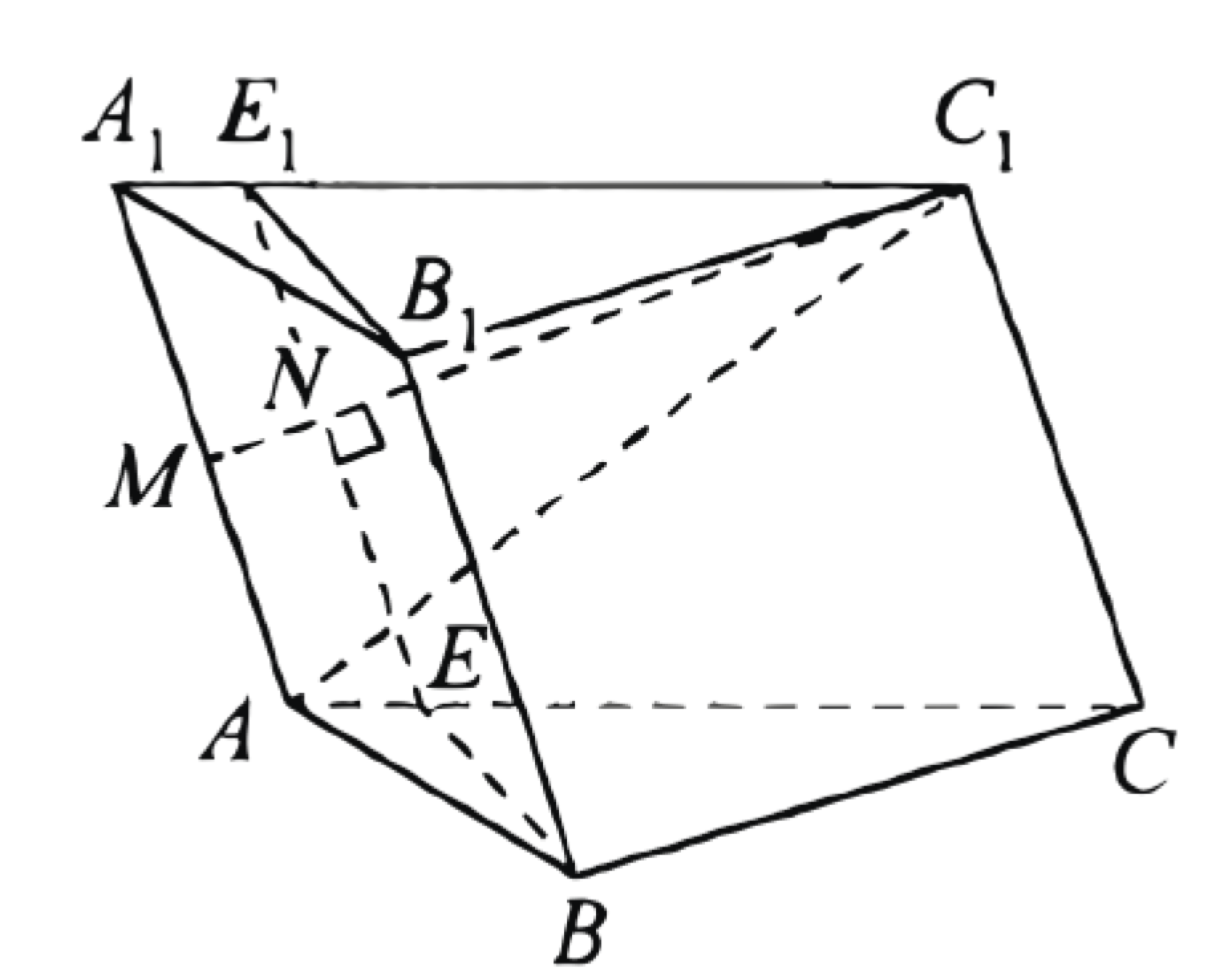
(ЕГЭ, 2022) Точка \(M\) - середина ребра \(A A_1\) треугольной призмы \(A B C A_1 B_1 C_1\), в основании которой лежит треугольник \(A B C\). Плоскость \(\alpha\) проходит через точки \(B\) и \(B_1\) перпендикулярно прямой \(C_1 M\).
a) Докажите, что одна из диагоналей грани \(A C C_1 A_1\) равна одному из рёбер этой грани.
б) Найдите расстояние от точки \(C\) до плоскости \(\alpha\), если плоскость \(\alpha\) делит ребро \(A C\) в отношении \(1: 5\), считая от вершины \(A, A C=20, A A_1=32\).
Решение
a) Пусть плоскость \(\alpha\) пересекает прямые \(A C\) и \(A_1 C_1\) в точках \(E\) и \(E_1\) соответственно.
Поскольку ребро \(A A_1\) параллельно ребру \(B B_1\) и содержащей его плоскости \(\alpha\), оно также параллельно прямой \(E E_1\).
Плоскость \(\alpha\) и лежащая в ней прямая \(E E_1\) перпендикулярны прямой \(C_1 M\), значит, отрезок \(C_1 M\) - высота треугольника \(A A_1 C_1\).
Отрезок \(C_1 M\) также является медианой этого треугольника, следовательно, треугольник \(A A_1 C_1\) равнобедренный, а диагональ \(A C_1\) грани \(A C C_1 A_1\) равна ребру \(A_1 C_1\).
б) Ребро \(C C_1\) параллельно ребру \(B B_1\) и содержащей его плоскости \(\alpha\), значит, расстояние от точки \(C\) до плоскости \(\alpha\) равно расстоянию от точки \(C_1\) до плоскости \(\alpha\), которое равно расстоянию от точки \(C_1\) до прямой \(E E_1\).
Пусть прямые \(C_1 M\) и \(E E_1\) пересекаются в точке \(N\).
Тогда \(C_1 N: C_1 M=C_1 E_1: C_1 A_1=\)
\(C E: C A=5: 6\).
В равнобедренном треугольнике \(A A_1 C_1\) высота \(C_1 M\) равна
\(\sqrt{A_1 C_1^2-A_1 M^2}=\sqrt{A C^2-\dfrac{A A_1^2}{4}}=12\),
откуда \(C_1 N=\dfrac{5}{6} C_1 M=10\) - искомое расстояние.
Ответ
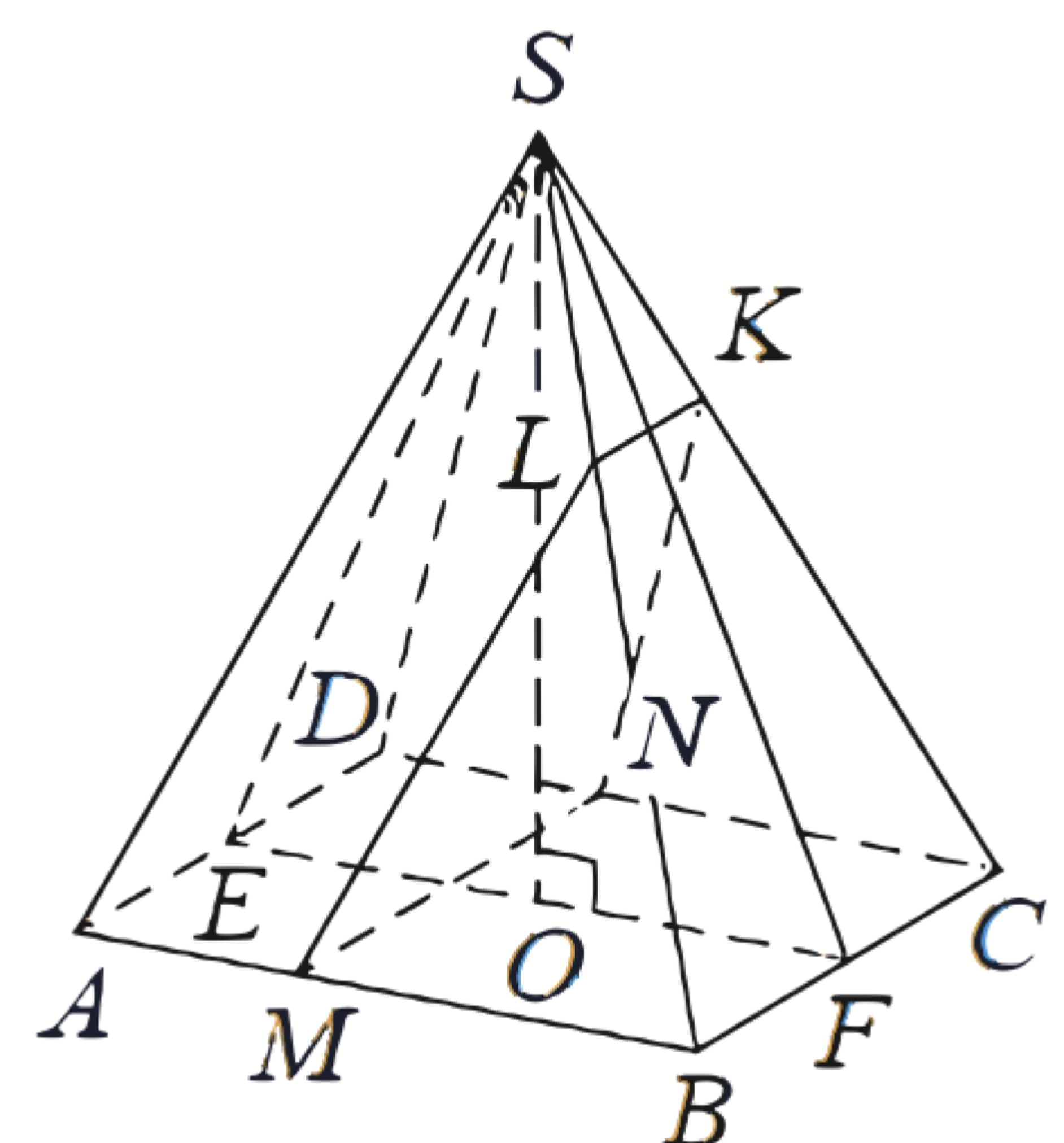
(ЕГЭ, 2021) В правильной четырёхугольной пирамиде \(S A B C D\) сторона основания \(A B\) равна 4, а боковое ребро \(S A\) равно 7. На рёбрах \(C D\) и \(S C\) отмечены точки \(N\) и \(K\) соответственно, причём \(D N: N C=S K: K C=1: 3\). Плоскость \(\alpha\) содержит прямую \(K N\) и параллельна прямой \(B C\).
a) Докажите, что плоскость \(\alpha\) параллельна прямой \(S A\).
б) Найдите угол между плоскостями \(\alpha\) и \(S B C\).
Решение
a) Пусть плоскость \(\alpha\) пересекает прямые \(S B\) и \(A B\) в точках \(L\) и \(M\) соответственно. Поскольку плоскость \(\alpha\) параллельна прямой \(B C\), прямые \(K L\), \(B C\) и \(M N\) параллельны.
Следовательно, \(S L: L B=S K: K C=D N: N C=A M: M B \text {. }\)
Таким образом, прямая \(L M\), лежащая в плоскости \(\alpha\), параллельна прямой \(S A\), а значит, плоскость \(\alpha\) параллельна прямой \(S A\).
б) Поскольку плоскость \(\alpha\) параллельна плоскости \(S A D\), искомый угол равен углу между плоскостями \(S A D\) и \(S B C\). Пусть точки \(E\) и \(F\) - середины рёбер \(A D\) и \(B C\) соответственно. Тогда прямые \(S F\) и \(E F\) перпендикулярны прямой \(B C\), а прямые \(S E\) и \(E F\) - прямой \(A D\).
Таким образом, плоскость \(S E F\) перпендикулярна прямым \(B C\) и \(A D\), а также содержащим их плоскостям \(S B C\) и \(S A D\) соответственно.
Значит, угол между плоскостями \(\alpha\) и \(S B C\) равен углу \(E S F\).
Высота \(S O\) пирамиды \(S A B C D\) лежит в плоскости \(S E F\), откуда
\(E O=2, S E=\sqrt{S A^2-\dfrac{A D^2}{4}}=3 \sqrt{5} ; \)
\(\sin \angle E S O=\dfrac{O E}{S E}=\dfrac{2 \sqrt{5}}{15} ;\)
\(\angle E S F=2 \angle E S O=2 \arcsin \dfrac{2 \sqrt{5}}{15} . \)
Ответ
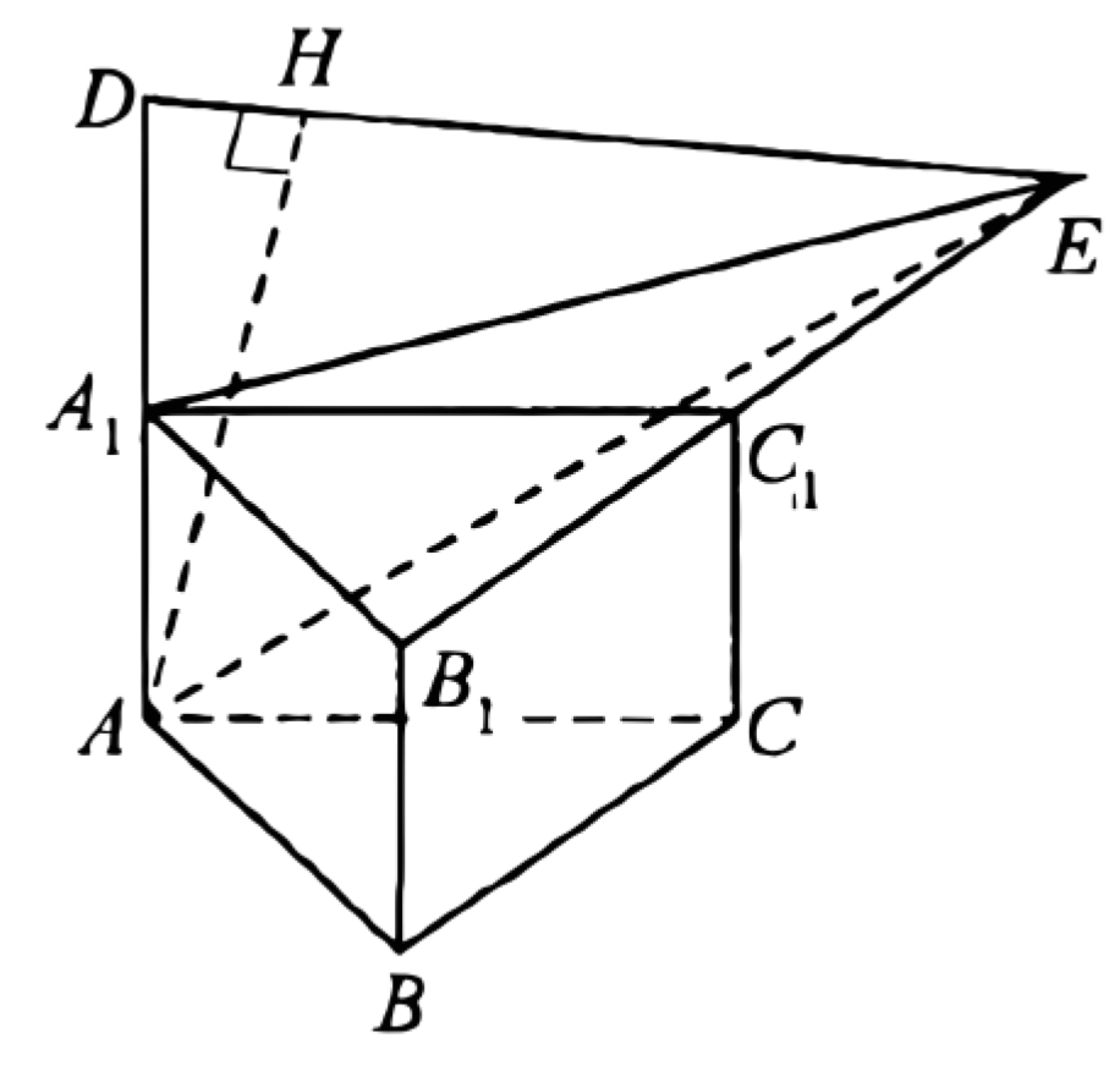
(ЕГЭ, 2021) В основании правильной треугольной призмы \(A B C A_1 B_1 C_1\) лежит треугольник \(A B C\). На прямой \(A A_1\) отмечена точка \(D\) так, что точка \(A_1\) середина отрезка \(A D\). На прямой \(B_1 C_1\) отмечена точка \(E\) так, что точка \(C_1-\) середина отрезка \(B_1 E\).
a) Докажите, что прямые \(A_1 B_1\) и \(D E\) перпендикулярны.
б) Найдите расстояние между прямыми \(A B\) и \(D E\), если \(A B=3, A A_1=1\).
Решение
a) Треугольник \(A_1 B_1 C_1\) правильный, поэтому угол \(A_1 C_1 E\) равен \(120^{\circ}\). B равнобедренном треугольнике \(A_1 C_1 E\) угол \(E A_1 C_1\) равен \(\dfrac{180^{\circ}-120^{\circ}}{2}=30^{\circ}\), а значит, угол \(E A_1 B_1\) равен \(90^{\circ}\).
Таким образом, прямая \(A_1 B_1\) перпендикулярна прямым \(A_1 D\) и \(A_1 E\). Значит, прямая \(A_1 B_1\) перпендикулярна плоскости \(A_1 D E\) и прямой \(D E\), лежащей в ней.
б) Прямая \(A B\) перпендикулярна прямым \(A D\) и \(D E\), поскольку прямые \(A B\) и \(A_1 B_1\) параллельны, следовательно, прямая \(A B\) перпендикулярна плоскости \(D A E\). Пусть отрезок \(A H\) - высота треугольника \(D A E\). Тогда отрезок \(A H\) перпендикулярен прямым \(A B\) и \(D E\), а его длина равна расстоянию \(h\) между прямыми \(A B\) и \(D E\).
В прямоугольном треугольнике \(A_1 B_1 E\) имеем:
\(B_1 E=2 A_1 B_1=6, \angle A_1 B_1 E=60^{\circ} ; \)
\(A_1 E=B_1 E \cdot \sin \angle A_1 B_1 E=3 \sqrt{3} .\)
В прямоугольном треугольнике \(D A_1 E\) имеем:
\(D A_1=A A_1=1 ; \)
\(D E=\sqrt{D A_1{ }^2+A_1 E^2}=2 \sqrt{7} .\)
Площадь треугольника \(D A E\) равна \(\dfrac{1}{2} \cdot A H \cdot D E=h \sqrt{7}\). С другой стороны, эта площадь равна \(\dfrac{1}{2} \cdot A_1 E \cdot D A=3 \sqrt{3}\). Таким образом, \(h \sqrt{7}=3 \sqrt{3}\), откуда \(h=\dfrac{3 \sqrt{21}}{7}\).
Ответ
(ЕГЭ, 2021) В правильной четырёхугольной пирамиде \(S A B C D\) сторона основания \(A D\) равна 10, высота \(S H\) равна 12. Точка \(K\) - середина бокового ребра \(S D\). Плоскость \(A K B\) пересекает боковое ребро \(S C\) в точке \(P\).
a) Докажите, что площадь четырёхугольника \(C D K P\) составляет \(\dfrac{3}{4}\) площади треугольника \(S C D\).
б) Найдите объём пирамиды \(A C D K P\).
Решение
a) Прямые \(A B\) и \(C D\) параллельны, следовательно, прямая \(A B\) параллельна плоскости \(S C D\) и не имеет с ней общих точек. Значит, прямые \(A B\) и \(K P\), лежащие в плоскости \(A K B\), не имеют общих точек, то есть они параллельны. Следовательно, прямая KP параллельна прямой \(C D\).
По теореме Фалеса получаем, что точка \(P\) середина ребра \(S C\).
Треугольники \(S P K\) и \(S C D\) подобны с коэффициентом подобия 2, а значит, площадь треугольника \(S P K\) в 4 раза меньше площади треугольника \(S C D\). Следовательно, площадь четырёхугольника \(C D K P\) составляет \(\dfrac{3}{4}\) площади треугольника \(S C D\).
б) Пирамиды \(A S C D\) и \(A C D K P\) имеют общую высоту, равную расстоянию \(h\) от точки \(A\) до плоскости \(S C D\). Пусть \(S_1\) - площадь треугольника \(S C D\). тогда площадь четырёхугольника \(C D K P\) равна \(\dfrac{3 S_1}{4}\).
Объём пирамиды \(A S C D\), с одной стороны, равен \(\dfrac{S_1 h}{3}\). С другой стороны, он равен \(\dfrac{1}{3} \cdot S H \cdot \dfrac{A D^2}{2}=\dfrac{1}{3} \cdot 12 \cdot 50=200\)
Значит, \(\dfrac{S_1 h}{3}=200\), откуда \(S_1 h=600\).
Объём пирамиды \(A C D K P\) равен \(\dfrac{1}{3} \cdot h \dfrac{3 S_1}{4}=\dfrac{S_1 h}{4}=150\).
Ответ
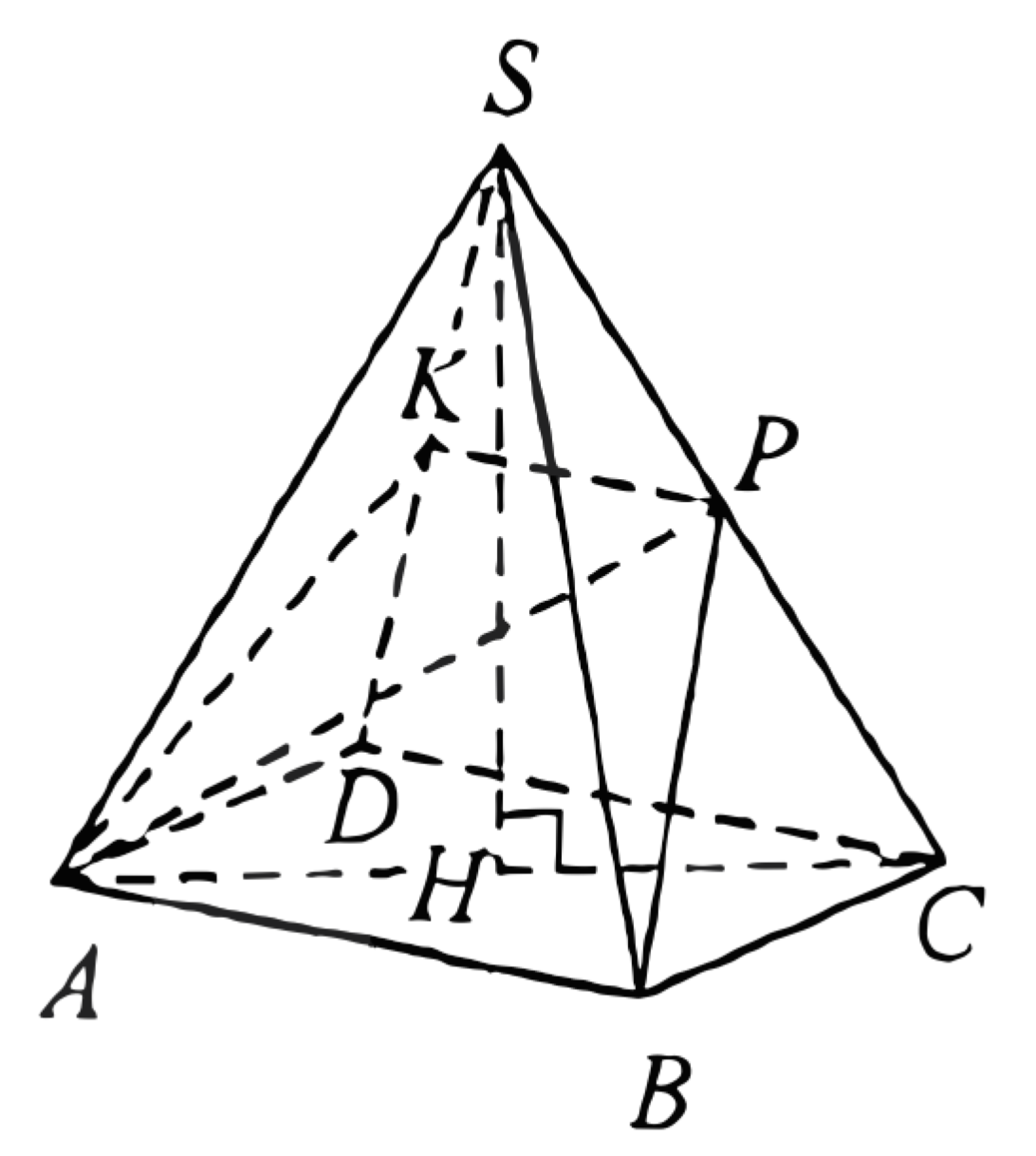
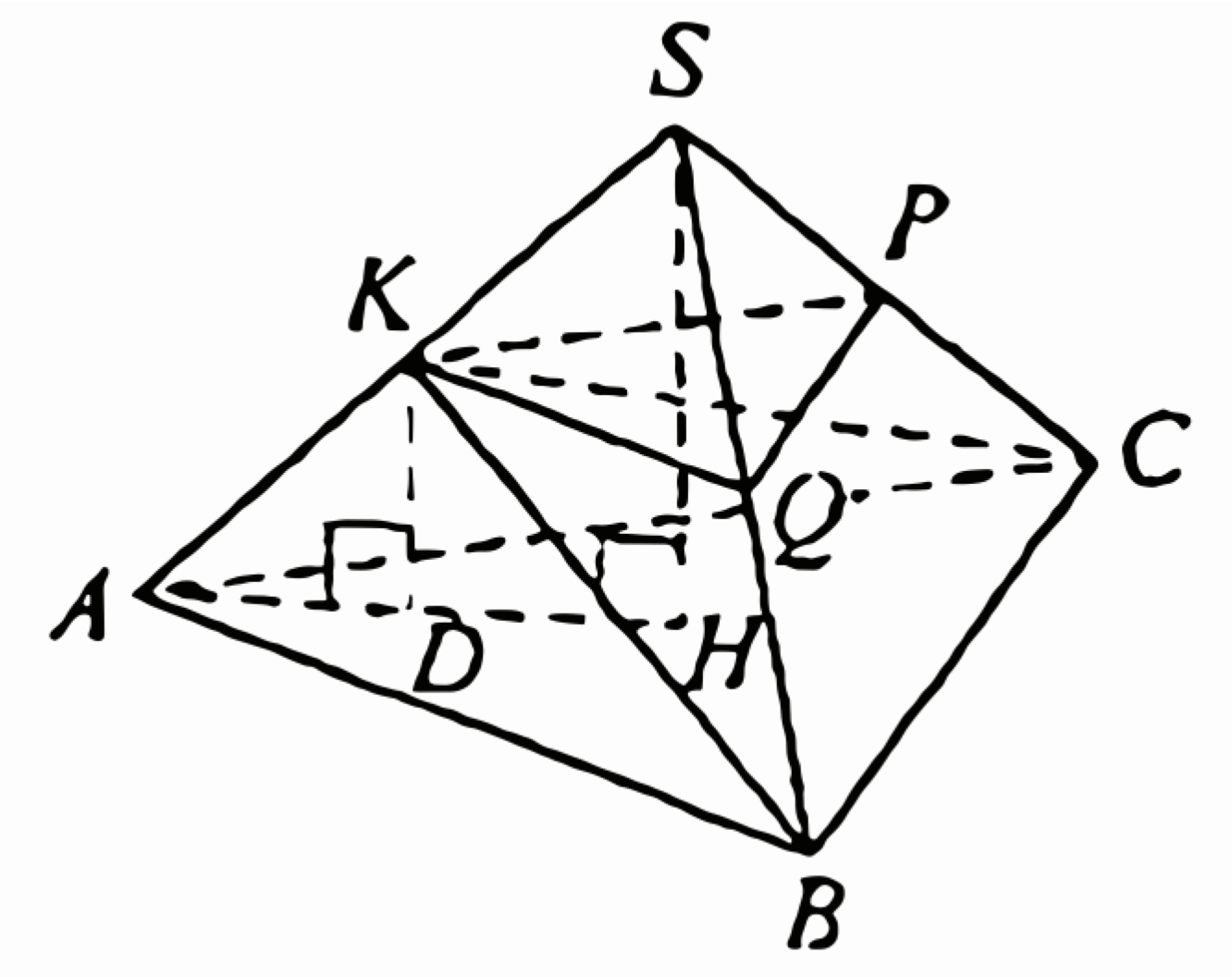
(ЕГЭ, 2021) В правильной треугольной пирамиде \(S A B C\) сторона основания \(A B\) равна 16 , высота \(S H\) равна 10. Точка \(K\) - середина бокового ребра \(S A\). Плоскость, параллельная плоскости \(A B C\), проходит через точку \(K\) и пересекает рёбра \(S B\) и \(S C\) в точках \(Q\) и \(P\) соответственно.
а) Докажите, что площадь четырёхугольника \(B C P Q\) составляет \(\dfrac{3}{4}\) площади треугольника \(S B C\).
б) Найдите объём пирамиды \(K B C P Q\).
Решение
a) Прямая \(K Q\) лежит в плоскости \(K Q P\), параллельной плоскости \(A B C\). Следовательно, прямые \(K Q\) и \(A B\) не имеют общих точек, а поскольку эти прямые лежат в одной и той же плоскости \(S A B\), они параллельны. Тогда по теореме Фалеса точка \(Q\) - середина ребра \(S B\). Аналогично точка \(P\) - середина ребра \(S C\).
Таким образом, отрезок \(Q P-\) средняя линия треугольника \(S B C\). Отсюда следует, что площадь треугольника \(S Q P\) составляет четверть площади треугольника \(S B C\), а тогда площадь четырёхугольника \(B C P Q\) составляет \(\dfrac{3}{4}\) площади треугольника \(S B C\).
б) Пусть отрезок \(K D\) - высота пирамиды \(K A B C\). Прямые \(S H\) и \(K D\) параллельны, а точка \(K\) - середина отрезка \(S A\), значит, отрезок \(K D\) является средней линией треугольника \(A S H\) и \(K D=\dfrac{S H}{2}\).
Объём пирамиды \(S A B C\) равен \(\dfrac{1}{3} \cdot S H \cdot \dfrac{\sqrt{3}}{4} A B^2=\dfrac{\sqrt{3}}{12} \cdot 10 \cdot 16^2=\dfrac{640 \sqrt{3}}{3}\). Объём пирамиды \(K A B C\) равен \(\dfrac{1}{3} \cdot \dfrac{S H}{2} \cdot \dfrac{\sqrt{3}}{4} A B^2=\dfrac{320 \sqrt{3}}{3}\). Значит, объём пирамиды \(K S B C\) равен \(\dfrac{640 \sqrt{3}}{3}-\dfrac{320 \sqrt{3}}{3}=\dfrac{320 \sqrt{3}}{3}\).
Пирамиды \(K S B C\) и \(K B C P Q\) имеют общую высоту, равную расстоянию \(h\) от точки \(K\) до плоскости \(S B C\). Пусть \(S_1\) - площадь треугольника \(S B C\), тогда площадь четырёхугольника \(B C P Q\) равна \(\dfrac{3 S_1}{4}\).
Объём пирамиды \(K S B C\) равен \(\dfrac{S_1 h}{3}\). С другой стороны, он равен \(\dfrac{320 \sqrt{3}}{3}\), откуда \(S_1 h=320 \sqrt{3}\).
Объём пирамиды \(K B C P Q\) равен \(\dfrac{1}{3} \cdot h \cdot \dfrac{3 S_1}{4}=\dfrac{S_1 h}{4}=80 \sqrt{3}\).
Ответ
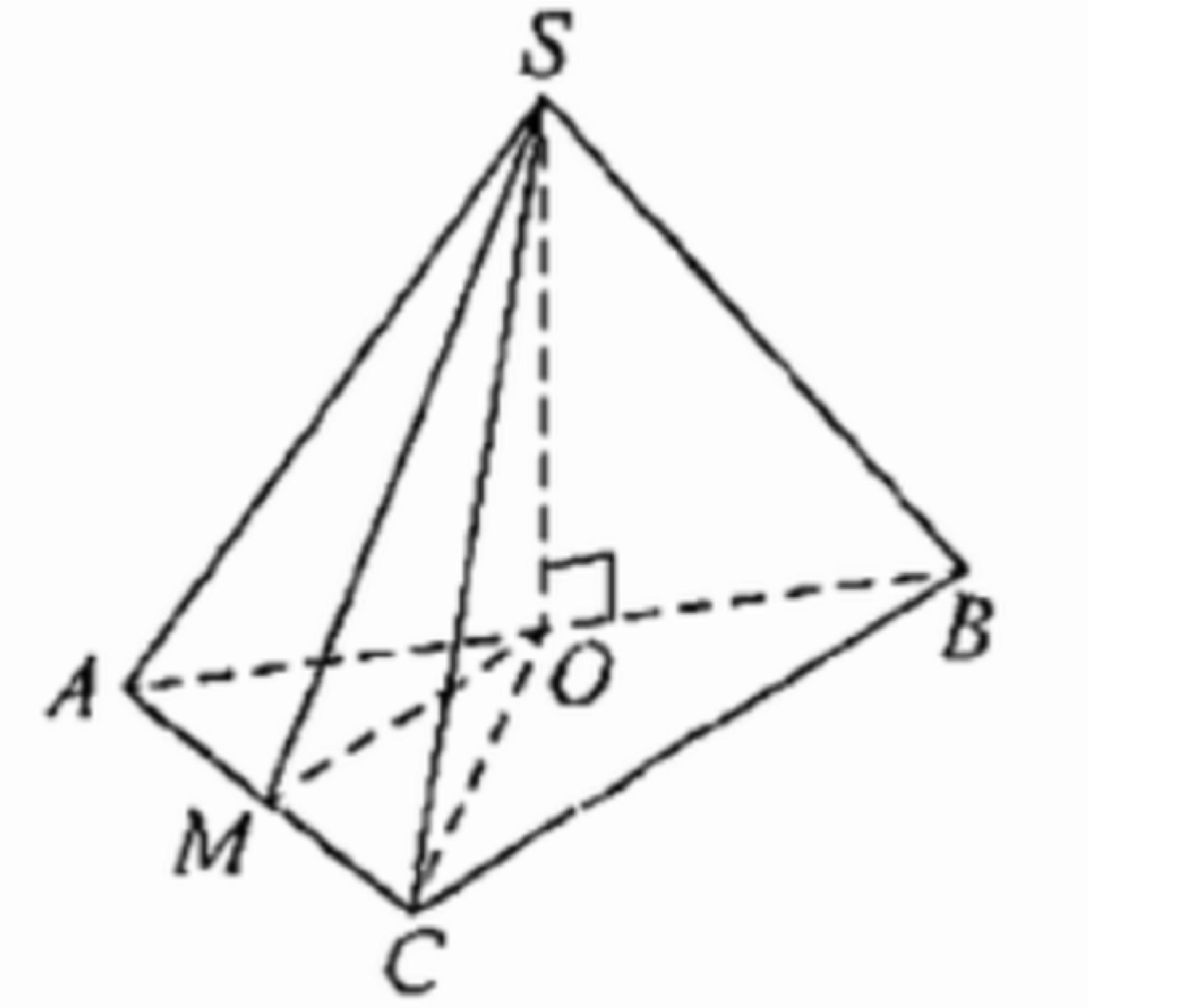
(ЕГЭ, 2021) В основании треугольной пирамиды \(S A B C\) лежит прямоугольный треугольник \(A B C\) с прямым углом \(C\). Основание высоты \(S O\) этой пирамиды является серединой ребра \(A B\).
а) Докажите, что \(S A=S C\).
б) Найдите угол между плоскостями \(S A C\) и \(A B C\), если \(A C=24, A B=30\), \(S A=17\).
Решение
а) Медиана, проведённая к гипотенузе прямоугольного треугольника, равна её половине, значит, \(A O=O C\). Следовательно, прямоугольные треугольники \(A S O\) и \(CSO\) равны по двум катетам, а значит, их гипотенузы \(S A\) и \(S C\) также равны.
б) Пусть точка \(M\) - середина стороны \(A C\). Поскольку треугольник \(SAC\) равнобедренный, прямые \(A C\) и \(S M\) перпендикулярны. Прямая \(S O\) перпендикулярна плоскости \(A B C\) и лежащей в ней прямой \(A C\). Получаем, что плоскость \(S M O\) перпендикулярна прямой \(A C\), а значит, и плоскостям \(A B C\) и \(S A C\), то есть угол \(S M O\) искомый.
В прямоугольном треугольнике \(A S O\) имеем:
\(S A=17, A O=\dfrac{A B}{2}=15 ;\)
\(S O=\sqrt{S A^2-A O^2}=8 .\)
Отрезок \(M O\) - средняя линия треугольника \(A B C\), значит,
\(M O=\dfrac{B C}{2}=\dfrac{\sqrt{A B^2-A C^2}}{2}=9 ;\)
\(\operatorname{tg} \angle S M O=\dfrac{S O}{M O}=\dfrac{8}{9} \).
Таким образом, угол между плоскостями \(S A C\) и \(A B C\) равен \(\operatorname{arctg} \dfrac{8}{9}\).