14. Стереометрия
Чтобы получить дополнительный функционал нужно войти.
(ЕГЭ, 2023) В четырёхугольной пирамиде \(S A B C D\) с основанием \(A B C D\) длины всех боковых рёбер равны длине ребра \(A D\), а длина каждого из рёбер \(A B, B C\) и \(C D\) ровно в два раза меньше, чем длина ребра \(A D\).
a) Докажите, что высота пирамиды проходит через середину ребра \(A D\).
б) Найдите, в каком отношении плоскость \(B M N\) делит высоту пирамиды, считая от вершины \(S\),
если точка \(M\) - середина ребра \(S D\), а точка \(N\) делит ребро \(S C\) в отношении \(S N: N C=3: 1\).
Решение
a) Пусть точка \(H\) - основание высоты пирамиды \(S A B C D\) (рис. 1). Прямоугольные треугольники \(A S H, B S H, C S H\) и \(D S H\) равны, поскольку катет \(S H\) общий, а гипотенузы \(S A, S B, S C\) и \(S D\) равны.
Значит, отрезки \(H A, H B, H C\) и \(H D\) равны, и четырёхугольник \(A B C D\) может быть вписан в окружность с центром \(H\).
Хорды \(A B\) и \(C D\) равны, значит, \(A B C D-\) равнобедренная трапеция.
Пусть \(H^{\prime}-\) середина \(A D\). Тогда четырёхугольники \(A B C H^{\prime}\) и \(B C D H^{\prime}\) - параллелограммы, поскольку \(A H^{\prime}=B C=H^{\prime} D\), а прямые \(B C\) и \(A D\) параллельны.
Следовательно, \(C H^{\prime}=A B=C D=H^{\prime} B\).
Значит, точка \(H^{\prime}\) равноудалена от всех вершин трапеции, а значит, точки \(H\) и \(H^{\prime}\) совпадают.
Таким образом, основание высоты пирамиды является серединой ребра \(A D\).
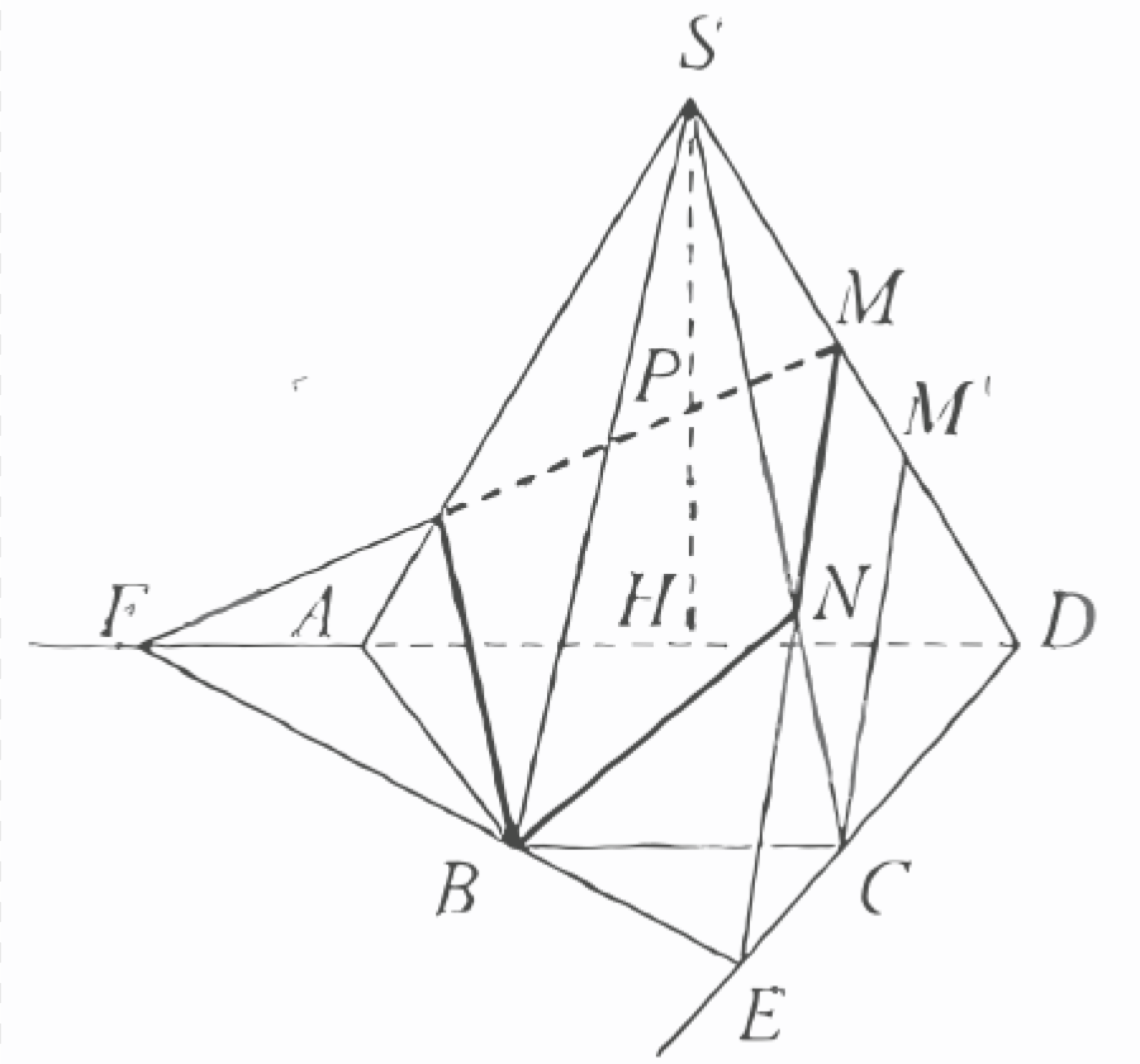
б) Пусть \(\quad\) прямая \(\quad M N\) пересекает продолжение \(C D\) в точке \(E\), прямая \(E B\)
пересекает продолжение \(A D\) в точке \(F\), а отрезок \(F M\) пересекает высоту \(S H\) в точке \(P\).
Рассмотрим точку \(M^{\prime}\) на ребре \(S D\) такую, что прямые \(M N\) и \(M^{\prime} C\) параллельны.
Тогда \(SM: MM^{\prime}= SN: NC=3: 1\).
Следовательно, \(E C: C D=M M^{\prime}: M^{\prime} D=1: 2 \text {. }\)
Значит, треугольники \(B C E\) и \(A D C\) подобны, поскольку \(\angle B C E=\angle A D C\), \(\dfrac{B C}{C E}=\dfrac{A D}{C D}=2\).
Таким образом, прямые \(B E\) и \(A C\) параллельны, поскольку \(\angle B E C=\angle A C D\)
Следовательно, \(F A: A D=E C: C D=1: 2\).
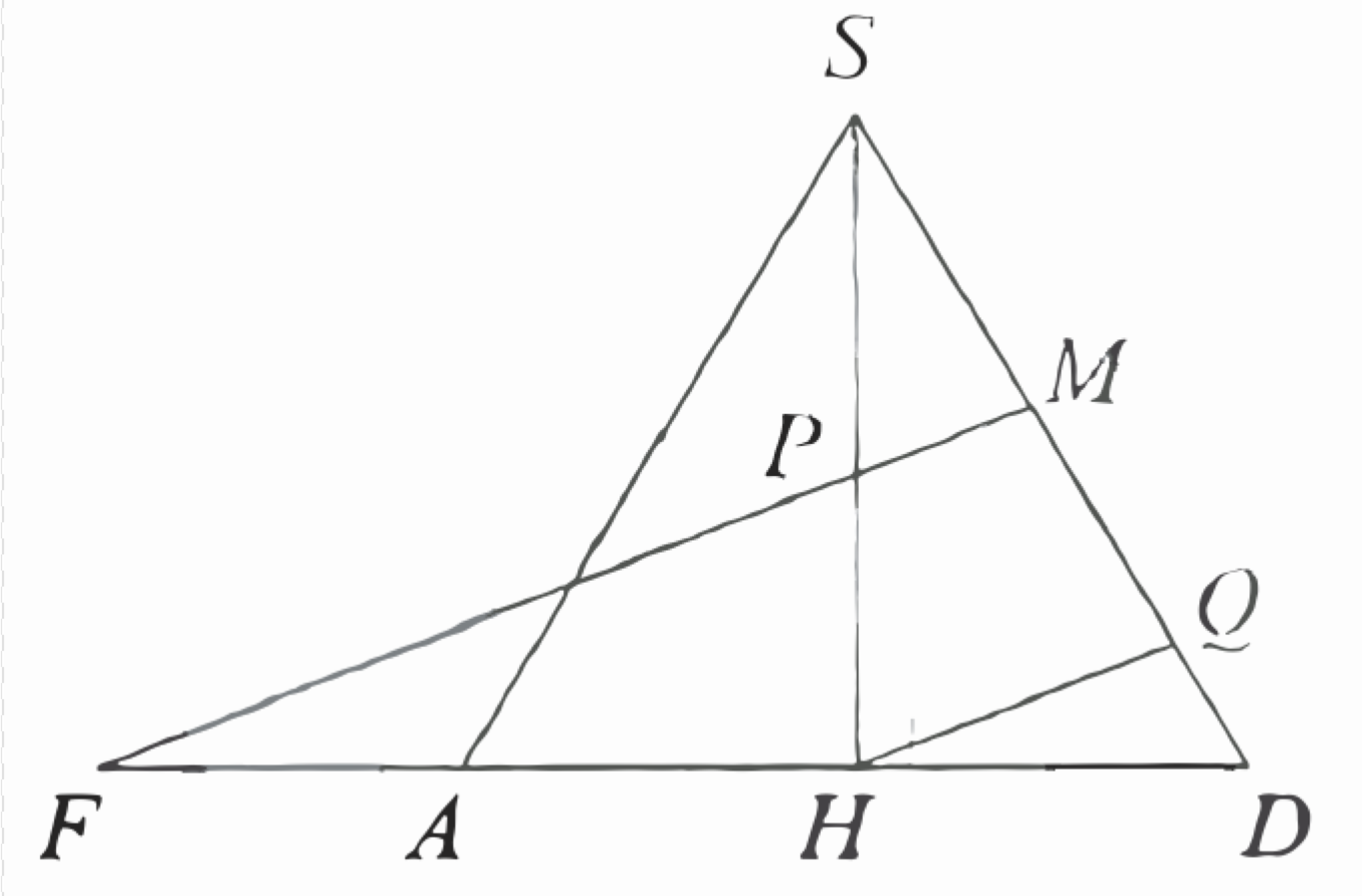
Рассмотрим точку \(Q\) на ребре \(S D\) такую, что прямые \(F M\) и \(H Q\) параллельны (рис. 2).
Тогда \(M Q: Q D=F H: H D=2: 1\).
Следовательно, \(S P: P H=S M: M Q=3: 2 \text {. }\)
Ответ
(ЕГЭ, 2022) Точка \(D\) выбрана вне плоскости правильного треугольника \(A B C\) так, что \(\cos \angle D A B=\cos \angle D A C=0,3\).
a) Докажите, что прямые \(A D\) и \(B C\) перпендикулярны.
б) Найдите расстояние между прямыми \(A D\) и \(B C\), если \(A B=6\).
Решение
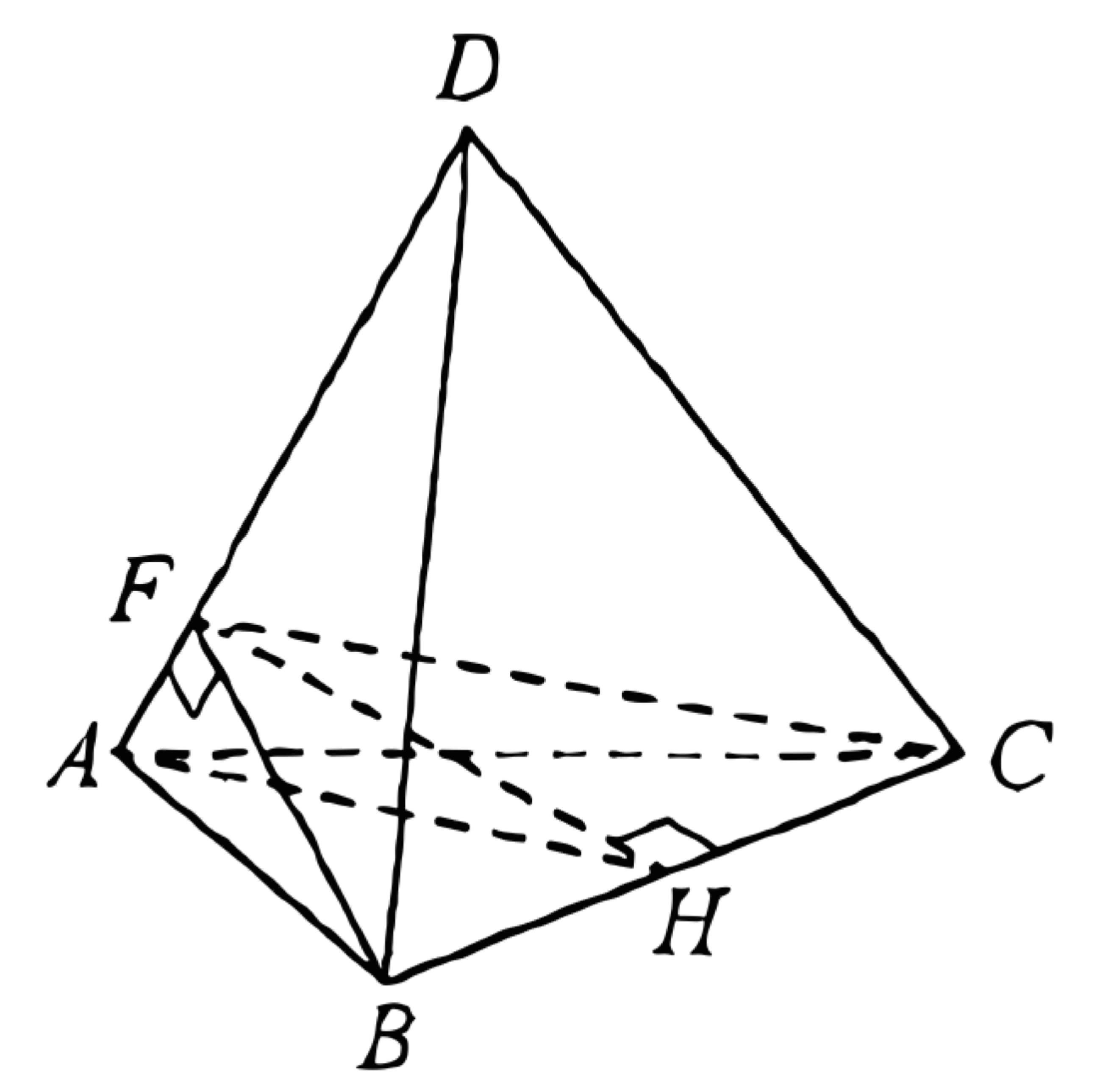
a) Пусть точка \(F\) - основание перпендикуляра, проведённого из точки \(B\) к прямой \(A D\). Треугольники \(A F B\) и \(A F C\) равны по двум сторонам и углу между ними, следовательно, \(\angle A F C=90^{\circ}\).
Прямые \(B F\) и \(C F\) перпендикулярны прямой \(A D\), значит, плоскость \(B F C\) и лежащая в ней прямая \(B C\) перпендикулярны прямой \(A D\).
б) Пусть точка \(H\) - основание перпендикуляра, проведённого из точки \(F\) к прямой \(B C\). Тогда отрезок \(F H\) перпендикулярен прямым \(A D\) и \(B C\), а его длина равна расстоянию между ними.
В равнобедренном треугольнике \(B F C\) высота \(F H\) является медианой, то есть точка \(H\) - середина отрезка \(B C\).
В правильном треугольнике \(A B C\) медиана \(A H=\dfrac{A B \sqrt{3}}{2}=3 \sqrt{3}\).
В прямоугольном треугольнике \(A F B\) катет \(A F\) равен \(A B \cdot \cos \angle D A B=\dfrac{9}{5}\).
В прямоугольном треугольнике \(A F H\)
\(F H=\sqrt{A H^2-A F^2}=\sqrt{27-\dfrac{81}{25}}=\)
\(\dfrac{3 \sqrt{66}}{5} .\)
Ответ
(ЕГЭ, 2022) Точка \(M\) - середина ребра \(S A\) правильной четырёхугольной пирамиды \(S A B C D\) с основанием \(A B C D\). Точка \(N\) лежит на ребре \(S B\), \(S N: N B=1: 2\).
a) Докажите, что плоскость \(C M N\) параллельна прямой \(S D\).
б) Найдите площадь сечения пирамиды \(S A B C D\) плоскостью \(C M N\), если все рёбра пирамиды равны 6.
Решение
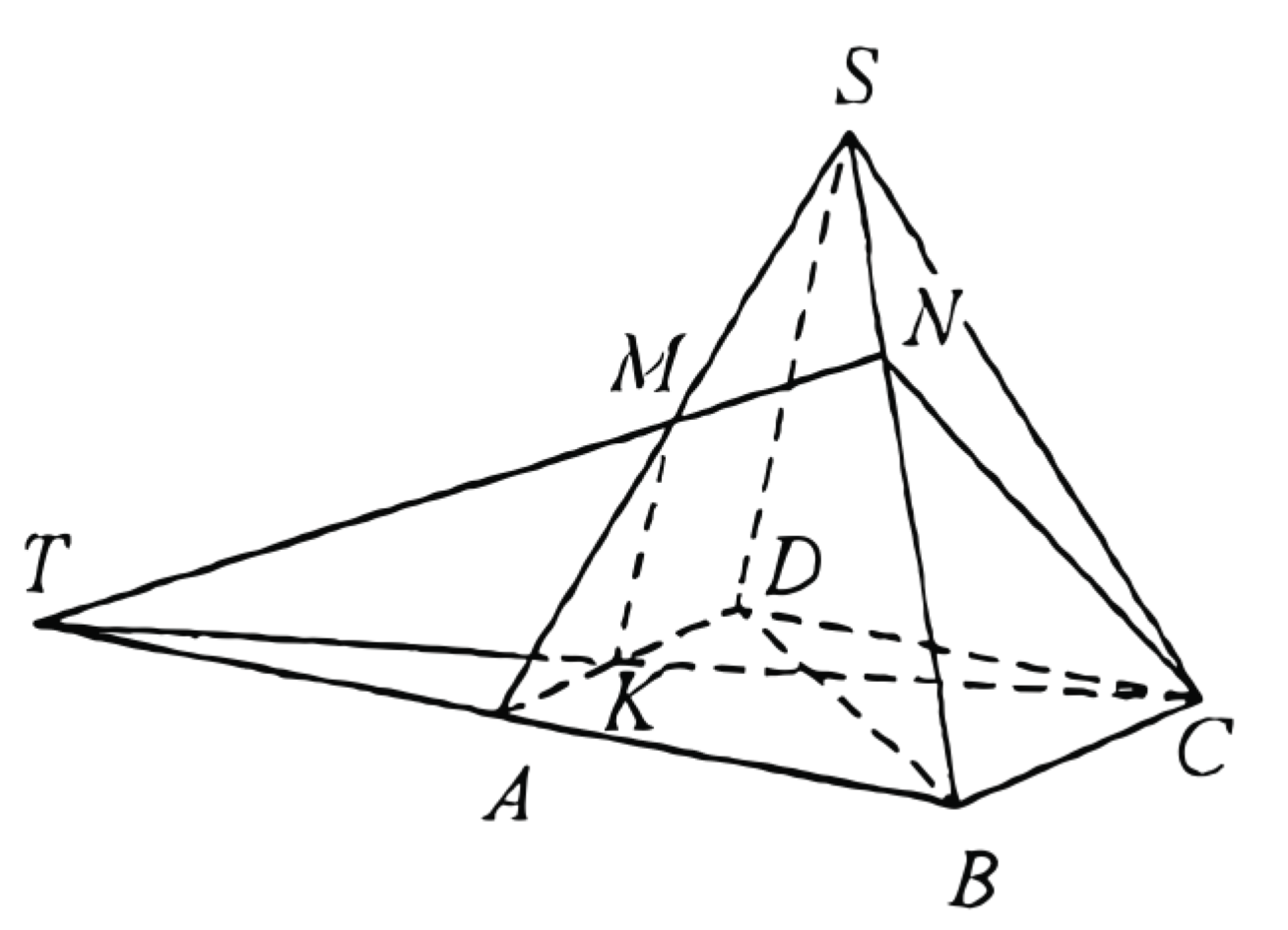
a) Пусть прямые \(A B\) и \(M N\) пересекаются в точке \(T\), а прямая \(T C\) пересекает ребро \(A D\) в точке \(K\) (рис. 1). Точка \(K\) лежит в плоскости \(C M N\).
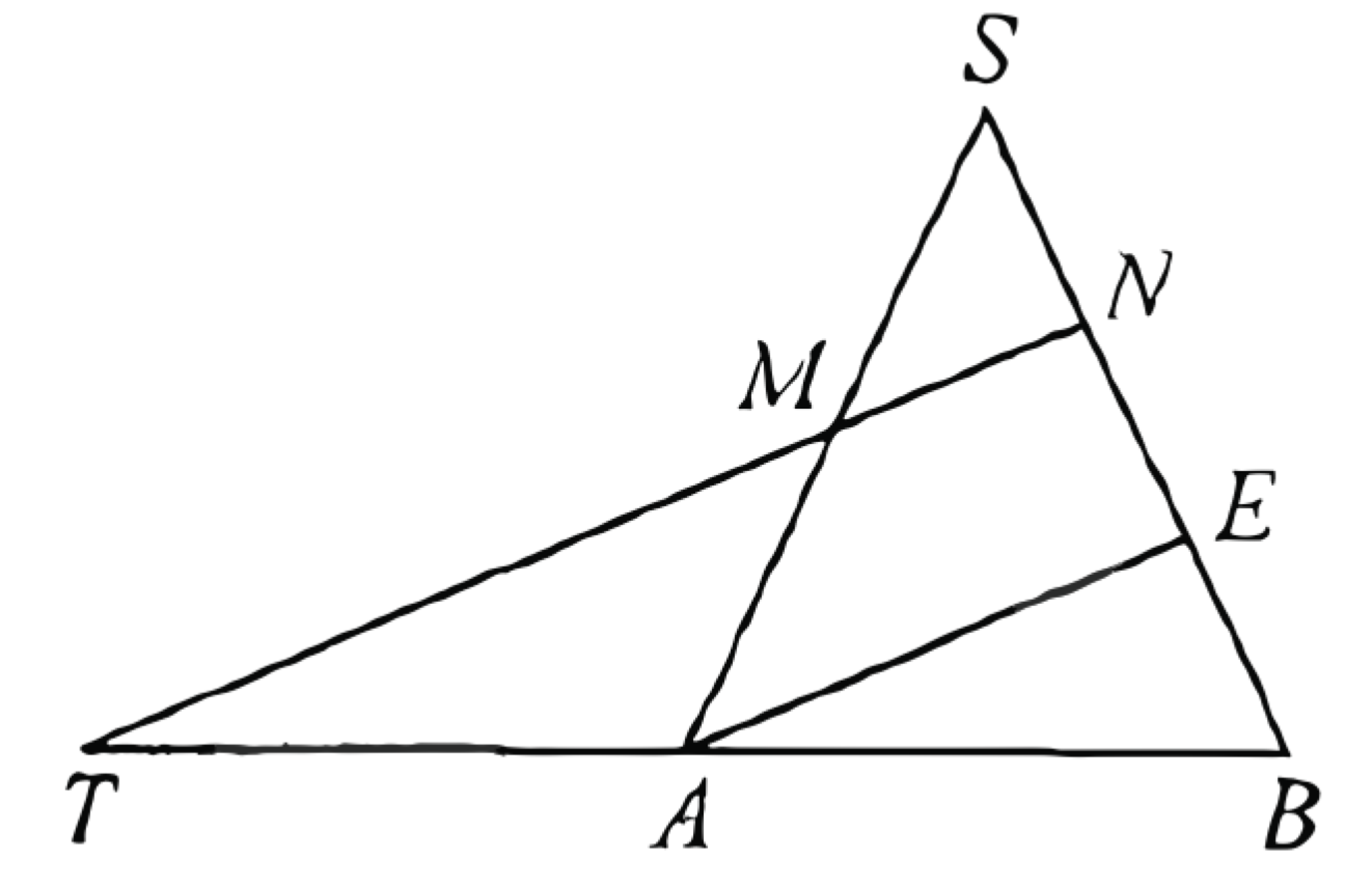
Рассмотрим плоскость \(S A B\) (рис. 2). Пусть точка \(E\) - середина отрезка \(N B\).
Тогда отрезок \(M N\) - средняя линия треугольника \(A S E\), а прямая \(M N\) параллельна прямой \(A E\). Значит, отрезок \(A E\) - средняя линия треугольника \(T N B\), откуда \(A T=A B\).
Прямоугольные треугольники \(T A K\) и \(C D K\) (см. рис. 1) равны по катету и противолежащему острому углу \((A T=C D, \angle T K A=\angle C K D),\) значит точка \(K\) - середина ребра \(A D\), то есть отрезок \(M K\) - средняя линия треугольника \(S A D\).
Следовательно, плоскость \(\quad C M N, \quad\) содержащая прямую \(M K\), параллельную прямой \(S D\), параллельна прямой \(S D\).
б) Четырёхугольник \(C N M K\) - сечение пирамиды \(S A B C D\) плоскостью \(C M N\). Отрезки \(M N\) и \(A E\) являются средними линиями треугольников \(A S E\) и \(T N B\) соответственно, значит, \(T N=2 A E=4 M N ; T M: T N=3: 4\).
Из треугольников \(S M N, S N C\) и \(T B C\) находим:
\(M N=\sqrt{M S^2+S N^2-2 M S \cdot S N \cdot \cos 60^{\circ}}=\)
\(\sqrt{9+4-6}=\sqrt{7} ; T N=4 M N=4 \sqrt{7},\)
\(C N=\sqrt{S C^2+S N^2-2 S C \cdot S N \cdot \cos 60^{\circ}}=\)
\(\sqrt{36+4-12}=2 \sqrt{7},\)
\(T C=\sqrt{T B^2+B C^2}=\sqrt{144+36}=6 \sqrt{5},\)
откуда
\(\cos \angle T N C=\dfrac{T N^2+C N^2-T C^2}{2 T N \cdot C N}=\)
\(\dfrac{112+28-180}{2 \cdot 4 \sqrt{7} \cdot 2 \sqrt{7}}=-\dfrac{5}{14} \)
\(\sin \angle T N C=\sqrt{1-\cos ^2 \angle T N C}=\)
\(\dfrac{\sqrt{171}}{14}=\dfrac{3 \sqrt{19}}{14} .\)
Площадь треугольника TNC равна
\(\dfrac{T N \cdot C N \cdot \sin \angle T N C}{2}=\)
\(\dfrac{4 \sqrt{7} \cdot 2 \sqrt{7} \cdot 3 \sqrt{19}}{28}=6 \sqrt{19} .\)
Площадь треугольника \(T M K\) составляет \(\dfrac{T M}{T N} \cdot \dfrac{T K}{T C}=\dfrac{3}{8}\) площади треугольника \(T N C\), значит, площадь четырёхугольника \(C N M K\) составляет \(\dfrac{5}{8}\) площади треугольника TNC и равна \(\dfrac{5}{8} \cdot 6 \sqrt{19}=\dfrac{15 \sqrt{19}}{4}\).
Ответ
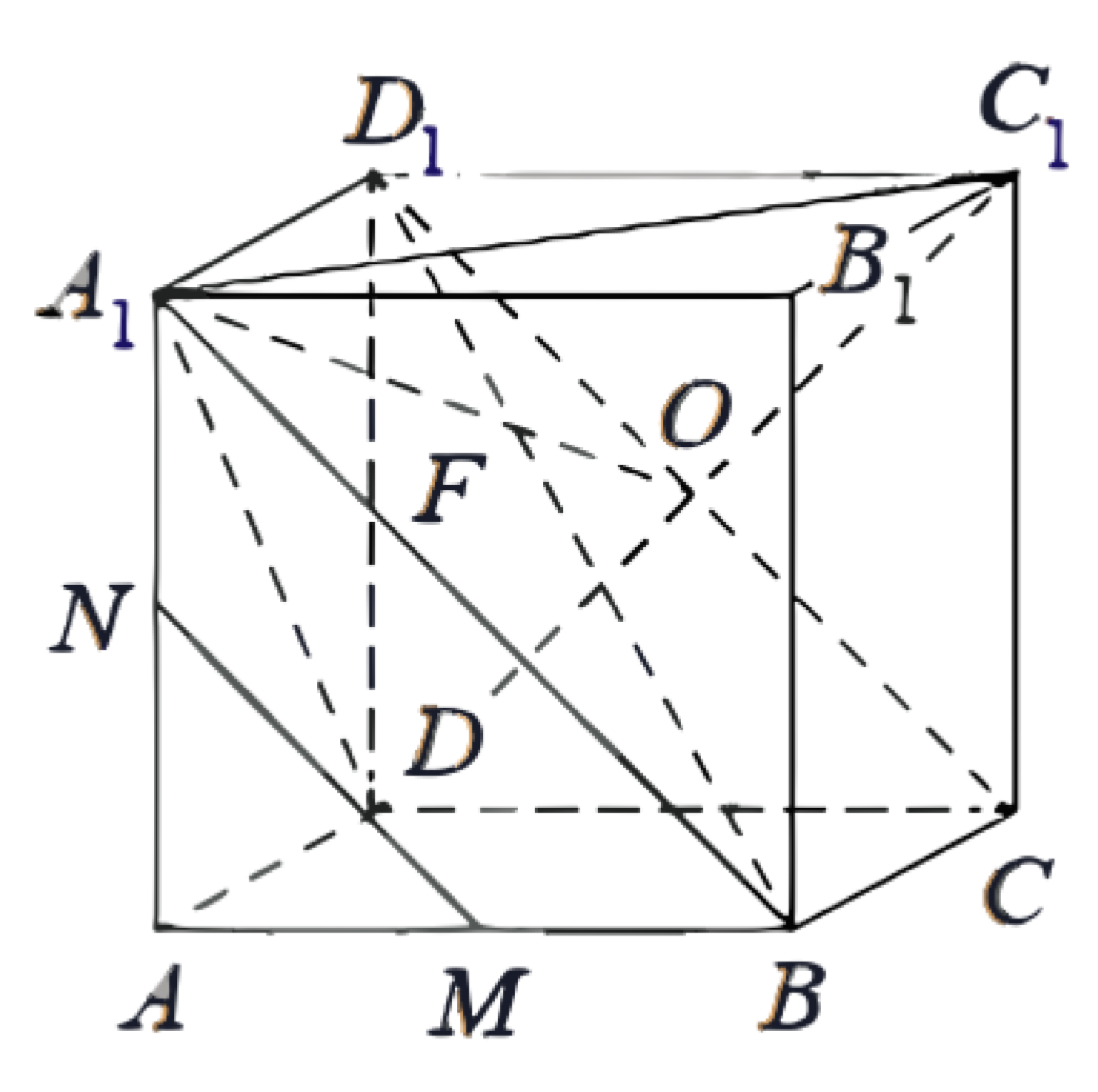
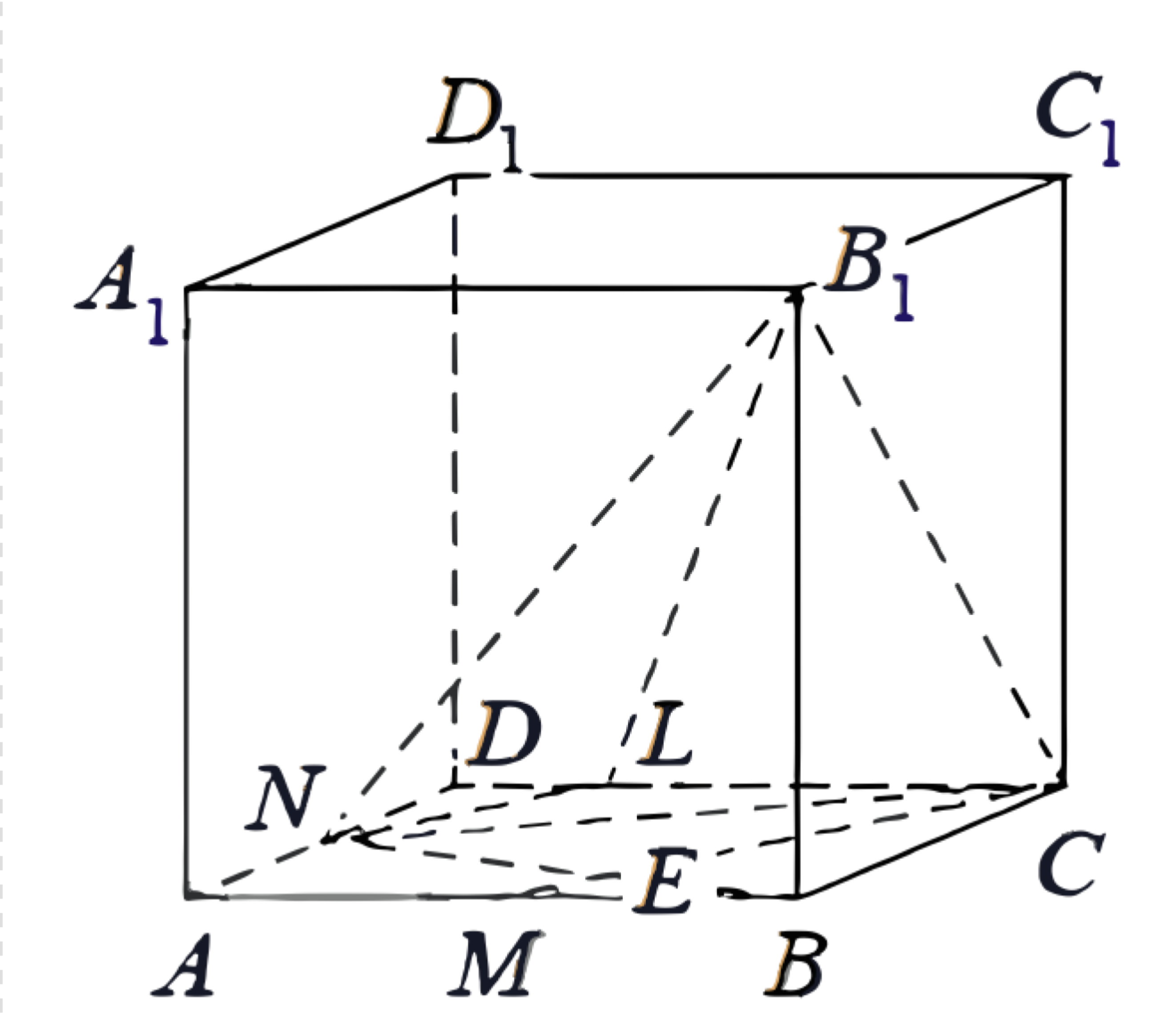
(ЕГЭ, 2022) В кубе \(A B C D A_1 B_1 C_1 D_1\) точки \(M\) и \(N\) - середины рёбер \(A B\) и \(A D\) соответственно.
a) Докажите, что прямые \(B_1 N\) и \(C M\) перпендикулярны.
б) Плоскость \(\alpha\) проходит через точки \(N\) и \(B_1\) параллельно прямой \(C M\). Найдите расстояние от точки \(C\) до плоскости \(\alpha\), если \(B_1 N=6\).
Решение
a) Пусть отрезки \(N B\) и \(M C\) пересекаются в точке \(E\).
Прямоугольные треугольники \(N A B\) и \(M B C\) равны по двум катетам, значит, \(\angle M E B=180^{\circ}-(\angle E M B+\angle E B M)=\)
\(180^{\circ}-(\angle E M B+\angle M C B)=90^{\circ}\).
Отрезок \(B N\) - проекция отрезка \(N B_1\) на плоскость \(A B C\). Следовательно, по теореме о трёх перпендикулярах прямые \(B_1 N\) и \(C M\) перпендикулярны.
б) Пусть плоскость \(\alpha\) пересекает ребро \(C D\) в точке \(L\). Прямые \(N L\) и \(C M\), лежащие в плоскости \(A B C\), параллельны, поскольку прямая \(N L\) лежит в плоскости \(\alpha\), параллельной прямой \(C M\). Следовательно, \(\angle D L N=\angle D C M=\angle B M C\), а значит, прямоугольные треугольники \(D L N\) и \(B M C\) подобны по острому углу. Получаем:
\(D L=B M \cdot \dfrac{D N}{B C}=\dfrac{A B}{2} \cdot \dfrac{A D}{2 B C}=\dfrac{C D}{4} .\)
Заметим, что \(\angle L N B_1=90^{\circ}\), поскольку прямая \(B_1 N\) перпендикулярна прямой \(N L\), параллельной прямой \(C M\). Пусть ребро куба равно \(a\).
Получаем: \(36=B_1 N^2=A N^2+A B^2+B B_1^2=\dfrac{9 a^2}{4},\)
откуда \(a=4 ; B B_1=a=4, D N=2, C L=3,\)
\(L N=\dfrac{a \sqrt{5}}{4}=\sqrt{5} \text {. }\)
Объём пирамиды \(C N L B_1\) равен \(\dfrac{1}{3} \cdot\left(\dfrac{1}{2} C L \cdot D N\right) \cdot B B_1=4\).
С другой стороны, объём этой пирамиды равен \(\dfrac{1}{3} \cdot\left(\dfrac{1}{2} N B_1 \cdot L N\right) \cdot x=x \sqrt{5}\), где \(x\) - расстояние от точки \(C\) до плоскости \(\alpha\). Из равенства \(x \sqrt{5}=4\) получаем \(x=\dfrac{4 \sqrt{5}}{5}\).
Ответ
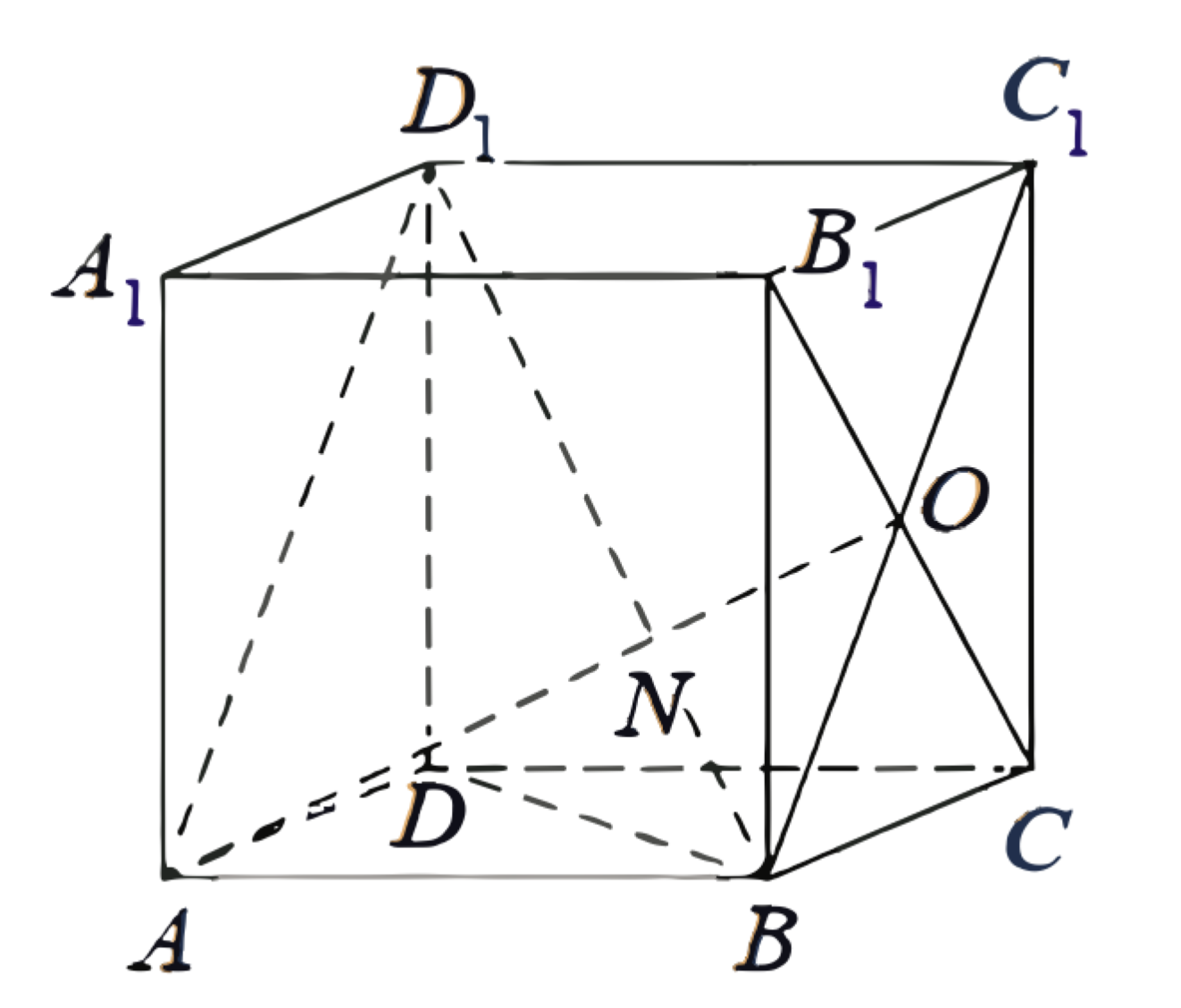
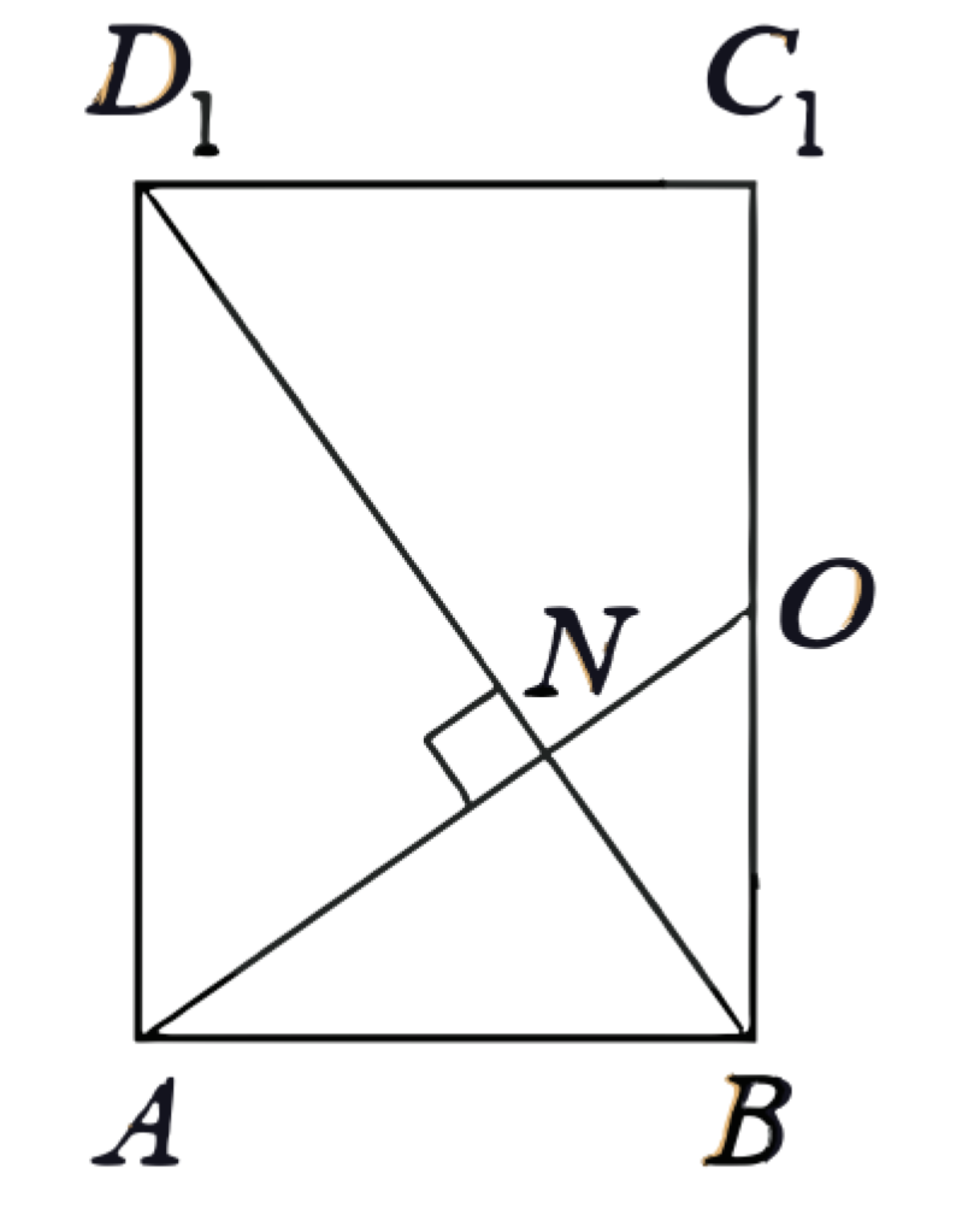
(ЕГЭ, 2022) В прямоугольном параллелепипеде \(A B C D A_1 B_1 C_1 D_1\) на диагонали \(B D_1\) отмечена точка \(N\) так, что \(B N: N D_1=1: 2\). Точка \(O\) - середина отрезка \(C B_1\).
a) Докажите, что прямая \(N O\) проходит через точку \(A\).
б) Найдите объём параллелепипеда \(A B C D A_1 B_1 C_1 D_1\), если длина отрезка \(N O\) равна расстоянию между прямыми \(B D_1\) и \(C B_1\) и равна \(\sqrt{2}\).
Решение
a) Точка \(O\) - середина диагоналей \(C B_1\) и \(B C_1\) прямоугольника \(B C C_1 B_1\) (рис. 1).
Следовательно, точка \(O\) лежит в плоскости \(A B C_1\).
Треугольники \(A D_1 N\) и \(O B N\) подобны по двум сторонам и углу между ними \(\left(\dfrac{A D_1}{B O}=2=\dfrac{D_1 N}{B N}\right.\),
\(\left.\angle A D_1 N=\angle A D_1 B=\angle D_1 B C_1=\angle N B O\right)\).
Получаем \(\angle A N O=\angle A N D_1+\angle D_1 N O=\)
\(\angle O N B+\angle D_1 N O= \angle D_1 N B=180^{\circ} \).
Таким образом, точка \(A\) лежит на прямой \(N O\).
б) Прямые \(B D_1\) и \(C B_1\) скрещивающиеся, а длина отрезка NO равна расстоянию между ними, значит, он перпендикулярен обеим этим прямым.
Таким образом, прямая \(C B_1\) перпендикулярна плоскости \(A B C_1\), поскольку она перпендикулярна лежащим в ней прямым \(A B\) и \(A O\). Следовательно, диагонали прямоугольника \(B C C_1 B_1\) перпендикулярны, то есть он является квадратом.
Из подобия треугольников \(A D_1 N\) и \(O B N\) следует, что \(A N=2 N O=2 \sqrt{2}\).
Отрезок \(B N\) - высота прямоугольного треугольника \(A B O\) (рис.2).
Получаем: \(B N=\sqrt{A N \cdot N O}=2 ; B D_1=6 ; \)
\(B O=\sqrt{B N^2+N O^2}=\sqrt{6} ; \)
\(A B=\sqrt{A O^2-O B^2}=2 \sqrt{3}\).
Значит, \(\quad B C=B B_1=\sqrt{2} \cdot B O=2 \sqrt{3}\). Таким образом, в прямоугольном параллелепипеде \(A B C D A_1 B_1 C_1 D_1\) все рёбра равны \(2 \sqrt{3}\). Следовательно, его объём равен \(24 \sqrt{3}\).
Ответ
(ЕГЭ, 2022) Точка \(O\) - точка пересечения диагоналей грани \(C D D_1 C_1\) куба \(A B C D A_1 B_1 C_1 D_1\). Плоскость \(D A_1 C_1\) пересекает диагональ \(B D_1\) в точке \(F\).
a) Докажите, что \(B F: F D_1=A_1 F: F O\).
б) Точки \(M\) и \(N\) - середины рёбер \(A B\) и \(A A_1\) соответственно. Найдите угол между прямой \(M N\) и плоскостью \(D A_1 C_1\)
Решение
a) Плоскость \(D A_1 C_1\) пересекает плоскость \(B C D_1\) по прямой \(A_1 O\), значит, точка \(F\) - это точка пересечения отрезков \(B D_1\) и \(A_1 O\). Прямые \(B A_1\) и \(C D_1\) параллельны, значит, треугольники \(D_1 F O\) и \(B F A_1\) подобны с коэффициентом подобия
\(\dfrac{A_1 F}{F O}=\dfrac{B F}{F D_1}=\dfrac{B A_1}{D_1 O}=2\).
Получаем, что \(B F: F D_1=A_1 F: F O=2: 1\).
б) Прямая \(C D_1\) является проекцией прямой \(B D_1\) на плоскость \(C D D_1\), а прямые \(C D_1\) и \(D C_1\) перпендикулярны, значит, по теореме о трёх перпендикулярах прямая \(B D_1\) перпендикулярна прямой \(D C_1\). Аналогично получаем, что прямая \(B D_1\) перпендикулярна прямой \(A_1 C_1\). Значит, прямая \(B D_1\) перпендикулярна плоскости \(D A_1 C_1\).
Отрезок \(M N\) - средняя линия треугольника \(A B A_1\), значит, он параллелен отрезку \(B A_1\). Угол между прямой \(M N\) и плоскостью \(D A_1 C_1\) равен углу между прямой \(B A_1\) и плоскостью \(D A_1 C_1\). Точка \(F\) - проекция точки \(B\) на плоскость \(D A_1 C_1\), следовательно, искомый угол равен углу \(B A_1 F\).
В прямоугольном треугольнике \(B A_1 D_1\) тангенс угла \(A_1 B D_1\) равен \(\dfrac{A_1 D_1}{B A_1}=\dfrac{1}{\sqrt{2}}\).
В прямоугольном треугольнике \(B A_1 F\) угол \(B A_1 F\) равен \(90^{\circ}-\angle A_1 B F=90^{\circ}-\operatorname{arctg} \dfrac{1}{\sqrt{2}}=\operatorname{arctg} \sqrt{2}\).