a) Пусть прямые \(A P\) и \(B B_1\) пересекаются в точке \(X\). Тогда точка \(U\) точка пересечения прямых \(X Q\) и \(B_1 C_1\).
Треугольники \(A X B\) и \(P X B_1\) подобны, откуда
\begin{equation*}
\frac{X B_1}{X B}=\frac{P B_1}{A B}=\frac{1}{2} ; B_1 X=B B_1=2 .
\end{equation*}

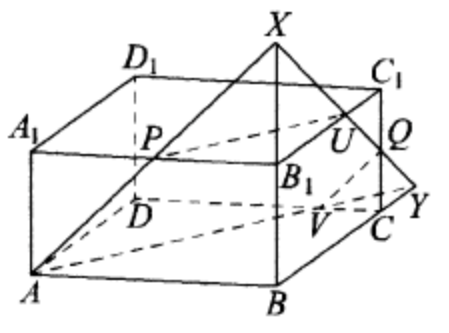
Треугольники \(B_1 X U\) и \(C_1 Q U\) подобны, откуда
\begin{equation*}
\frac{B_1 U}{C_1 U}=\frac{B_1 X}{C_1 Q}=2 ; B_1 U=2 C_1 U .
\end{equation*}

Значит, \(B_1 U: U C_1=2: 1\).

б) Пусть \(Y\) - точка пересечения прямых \(Q X\) и \(B C\), а \(V\) - точка пересечения прямых \(C D\) и \(A Y\). Тогда пятиугольник \(A P U Q V\) - сечение, площадь которого надо найти.
Треугольники \(C_1 U Q\) и \(C Y Q\) равны, откуда \(C Y=C_1 U=1\).
Треугольники \(A Y B\) и \(V Y C\) подобны, откуда \(\frac{V C}{A B}=\frac{C Y}{B Y}=\frac{1}{4} ; V C=\frac{A B}{4}=1\).
Четырёхугольник \(APUY\) - равнобедренная трапеция, в которой
\begin{equation*}
A P=P U=U Y=2 \sqrt{2}, A Y=4 \sqrt{2} .
\end{equation*}

Все стороны треугольника \(Q Y V\) равны \(\sqrt{2}\).
Высота трапеции \(A P U Y\) равна \(\sqrt{A P^2-\left(\frac{A Y-P U}{2}\right)^2}=\sqrt{6}\), а её площадь равна \(\frac{2 \sqrt{2}+4 \sqrt{2}}{2} \cdot \sqrt{6}=6 \sqrt{3}\). Площадь треугольника \(Q Y V\) равна \(\frac{\sqrt{3}}{2}\). Значит, искомая площадь равна \(6 \sqrt{3}-\frac{\sqrt{3}}{2}=\frac{11 \sqrt{3}}{2}\).

a) Пусть \(R\) - точка пересечения прямых \(P Q\) и \(A_1 C_1\), а \(K\) - середина \(B_1 C_1\).

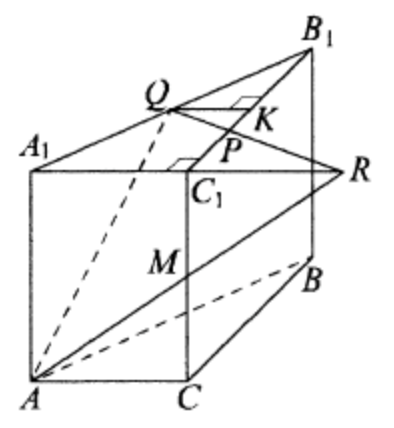
Тогда точка \(M\) - точка пересечения прямых \(A R\) и \(C C_1\). Треугольники \(P K Q\) и \(P C_1 R\) подобны, откуда
\begin{equation*}
\frac{C_1 R}{K Q}=\frac{C_1 P}{K P}=2 ; C_1 R=2 K Q=A_1 C_1=4 \text {. }
\end{equation*}

Отрезок \(C_1 M\) - средняя линия треугольника \(A A_1 R\), поскольку \(A_1 C_1=C_1 R\) и прямые \(A A_1\) и \(C C_1\) параллельны. Значит,
\begin{equation*}
C_1 M=\frac{A_1 A}{2}=\frac{C_1 C}{2},
\end{equation*}

то есть \(M\) - середина \(C C_1\).

б) Расстояние от точки \(A_1\) до плоскости \(A P Q\) равно высоте \(h\) пирамиды \(A_1 A Q R\), опущенной из вершины \(A_1\).
С одной стороны, объём пирамиды \(A_1 A Q R\) равен
\begin{equation*}
\frac{1}{3} \cdot \frac{B_1 C_1}{2} S_{A A_1 R}=\frac{1}{3} \cdot \frac{B_1 C_1}{2} \cdot \frac{1}{2} A \dot{A}_1 \quad A_1 R=\frac{128 \sqrt{2}}{3} .
\end{equation*}

С другой стороны, объём пирамиды \(A_1 A Q R\) равен \(\frac{1}{3} \cdot h \cdot S_{A Q R}\). Значит,
\begin{equation*}
h=\frac{128 \sqrt{2}}{S_{A Q R}} .
\end{equation*}

В треугольнике \(A Q R\) находим стороны:
\begin{equation*}
A Q=Q R=10, A R=4 \sqrt{6} .
\end{equation*}

Площадь равнобедренного треугольника \(A Q R\) равна
\begin{equation*}
S_{A Q R}=\frac{1}{2} A R \sqrt{A Q^2-\frac{A R^2}{4}}=4 \sqrt{114} .
\end{equation*}

Следовательно,
\begin{equation*}
h=\frac{128 \sqrt{2}}{4 \sqrt{114}}=\frac{32 \sqrt{57}}{57} .
\end{equation*}

a) Пусть прямые \(A P\) и \(B C\) пересекаются в точке \(R\).

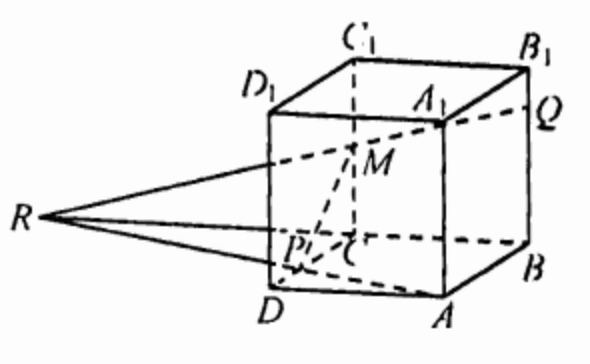
Тогда точка \(M\) точка пересечения прямых \(Q R\) и \(C C_1\).
Треугольники \(A R B\) и \(P R C\) подобны, откуда \(\frac{R C}{R B}=\frac{P C}{A B}=\frac{2}{3} ; R C=2 B C=24\).
Треугольники \(Q R B\) и \(M R C\) подобны, откуда \(\frac{M C}{Q B}=\frac{R C}{R B}=\frac{2}{3} ; M C=\frac{2}{3} Q B=6\).
Значит, \(M\) - середина \(C C_1\).

б) Расстояние от точки \(C\) до плоскости \(A P Q\) равно высоте \(h\) пирамиды \(C P R M\), опущенной из вершины \(C\). Объём пирамиды \(C P R M\), с одной стороны, равен
\begin{equation*}
\frac{1}{3} \cdot R C \cdot S_{M P C}=\frac{1}{3} \cdot R C \cdot \frac{1}{2} P C \cdot C M=192 .
\end{equation*}

С другой стороны, объём пирамиды \(C P R M\) равен \(\frac{1}{3} \cdot h \cdot S_{R P M}\). Значит,
\begin{equation*}
h=\frac{3 \cdot 192}{S_{R P M}} .
\end{equation*}

В треугольнике \(R P M\) находим стороны: \(R P=8 \sqrt{10}, R M=6 \sqrt{17}, M P=10\). По теореме косинусов
\begin{equation*}
\cos \angle M R P=\frac{M R^2+R P^2-M P^2}{2 M R \cdot P R}=\frac{12}{\sqrt{170}},
\end{equation*}

откуда \(\sin \angle M R P=\frac{\sqrt{26}}{\sqrt{170}}\).
Площадь треугольника \(R P M\) равна \(S_{R P M}=\frac{1}{2} \cdot 6 \sqrt{17} \cdot 8 \sqrt{10} \cdot \frac{\sqrt{26}}{\sqrt{170}}=24 \sqrt{26}\).
Следовательно, \(h=\frac{3 \cdot 192}{24 \sqrt{26}}=\frac{12 \sqrt{26}}{13}\).

a) Пусть прямые \(A_1 Q\) и \(B B_1\) пересекаются в точке \(R\).

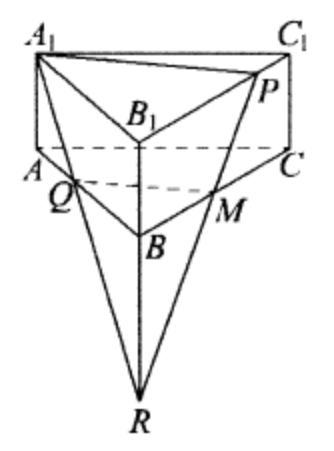
Тогда точка \(M\) - точка пересечения прямых \(P R\) и \(B C\).
Треугольники \(A_1 B_1 R\) и \(Q B R\) подобны, откуда
\begin{equation*}
\frac{B R}{B_1 R}=\frac{Q B}{A_1 B_1}=\frac{2}{3} ; R B=2 B B_1=4 .
\end{equation*}

Треугольники \(P B_1 R\) и \(M B R\) подобны, откуда
\begin{equation*}
\frac{B M}{B_1 P}=\frac{B R}{B_1 R}=\frac{2}{3} ; B M=\frac{2}{3} B_1 P=6 .
\end{equation*}

Значит, \(M\) - середина \(B C\).

б) Расстояние от точки \(B\) до плоскости \(A_1 P Q\) равно высоте \(h\) пирамиды \(B R Q M\), опущенной из вершины \(B\). Объём пирамиды \(B R Q M\), с одной стороны, равен
\begin{equation*}
\frac{1}{3} \cdot R B \cdot S_{Q M B}=\frac{1}{3} \cdot R B \cdot \frac{1}{2} B Q \cdot B M \cdot \sin 60^{\circ}=16 \sqrt{3} .
\end{equation*}

С другой стороны, объём пирамиды \(B R Q M\) равен \(\frac{1}{3} \cdot h \cdot S_{Q M R}\). Значит,
\begin{equation*}
h=\frac{3 \cdot 16 \sqrt{3}}{S_{Q M R}} .
\end{equation*}

В треугольнике \(Q M R\) находим стороны:
\begin{equation*}
Q M=M R=2 \sqrt{13}, Q R=4 \sqrt{5} .
\end{equation*}

Площадь равнобедренного треугольника \(Q M R\) равна
\begin{equation*}
S_{Q M R}=\frac{1}{2} \cdot Q R \sqrt{Q M^2-\frac{Q R^2}{4}}=8 \sqrt{10} \text {. }
\end{equation*}

Следовательно, \(h=\frac{316 \sqrt{3}}{8 \sqrt{10}}=\frac{3 \sqrt{30}}{5}\).