14. Стереометрия
Чтобы получить дополнительный функционал нужно войти.
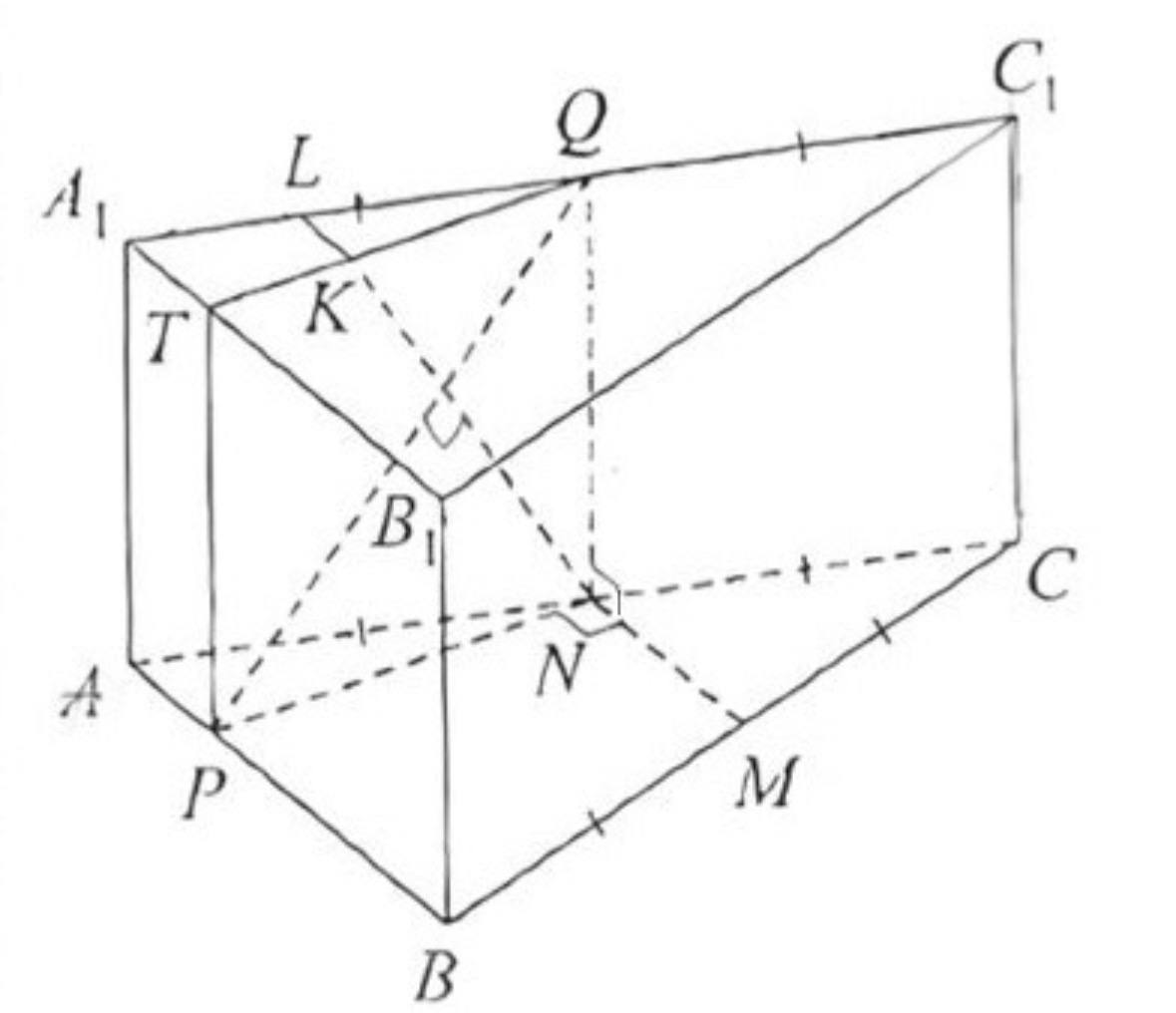
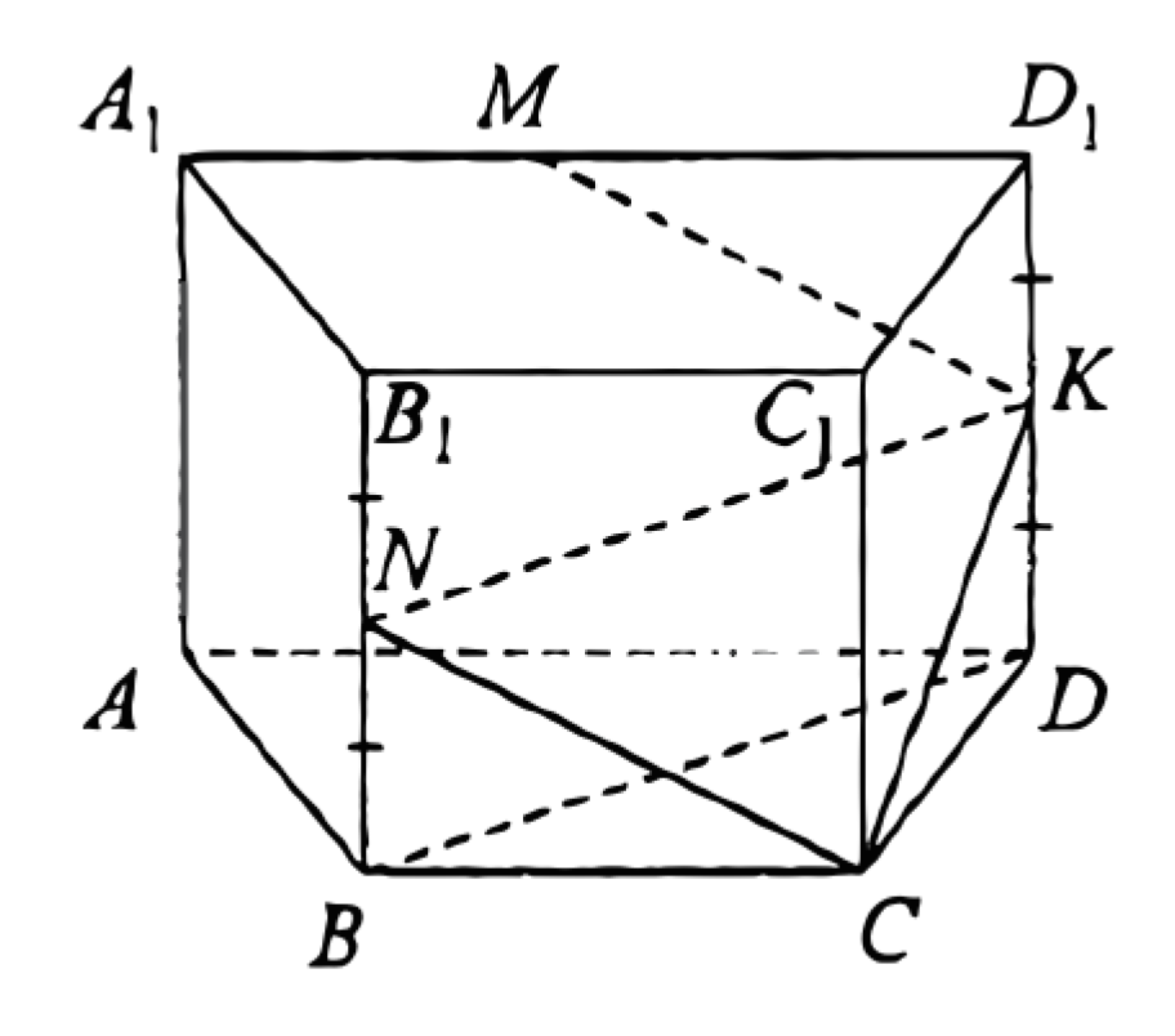
(ЕГЭ, 2023) В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит параллелограмм \(A B C D\). На рёбрах \(A_1 B_1, B_1 C_1\) и \(B C\) отмечены точки \(M, K\) и \(N\) соответственно, причём \(B_1 K: K C_1=1: 2\). Четырёхугольник \(A M K N\) - равнобедренная трапеция с основаниями 2 и 3.
a) Докажите, что точка \(N\) - середина ребра \(B C\).
б) Найдите площадь трапеции \(A M K N\), если объём призмы равен 12 , а высота призмы равна 2.
Решение
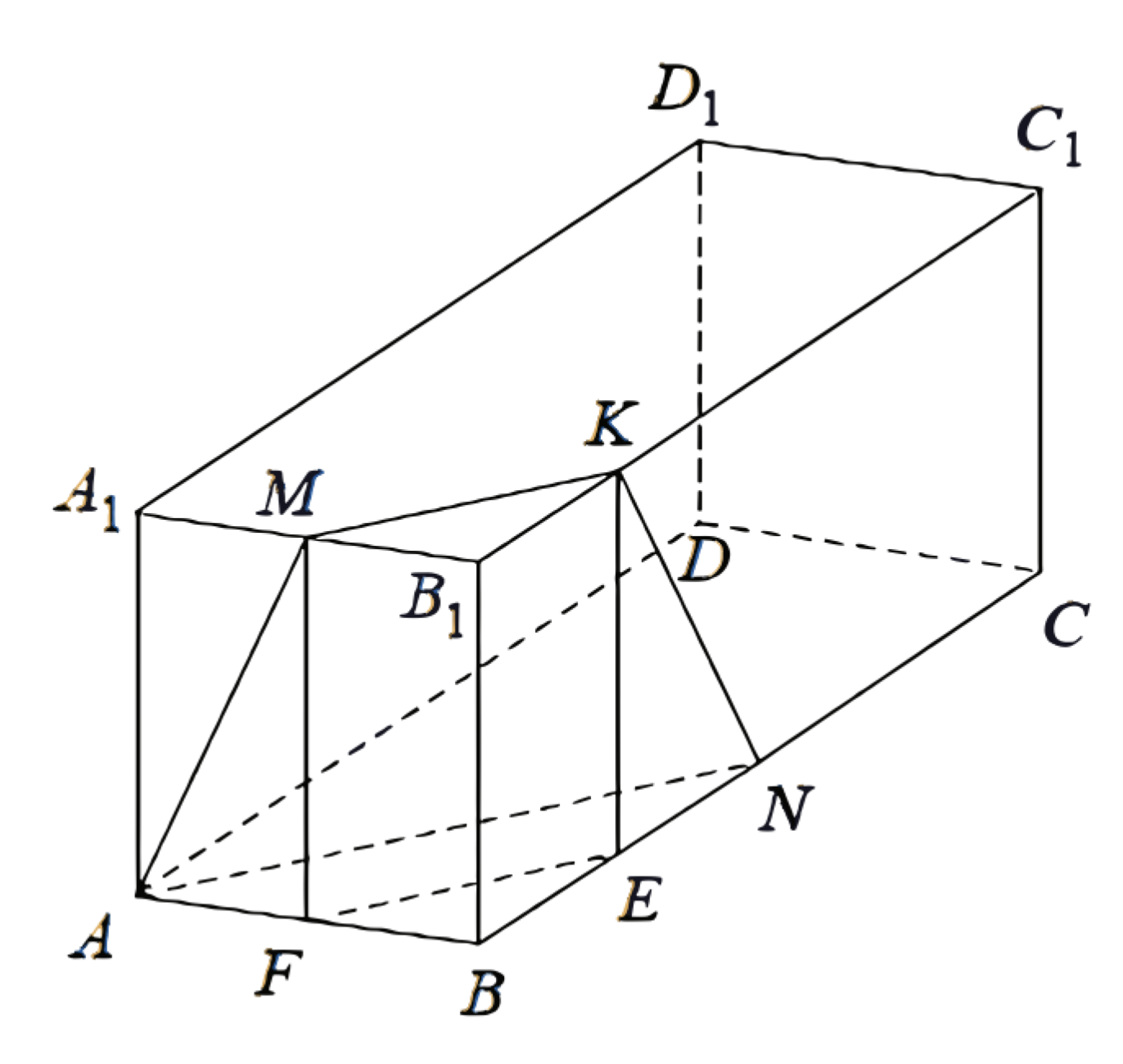
a) Пусть отрезки \(M F\) и \(K E\) - высоты призмы \(A B C D A_1 B_1 C_1 D_1 \quad\)
Тогда отрезок FE параллелен и равен отрезку \(M K\), а значит, параллелен отрезку \(A N\) и равен \(\dfrac{2}{3} A N\).
Следовательно, треугольники \(F B E\) и \(A B N\) подобны с коэффициентом \(\dfrac{2}{3}\).
Значит, \(B N=\dfrac{3}{2} B E=\dfrac{3}{2} B_1 K=\dfrac{1}{2} B_1 C_1=\dfrac{1}{2} B C\).
Следовательно, точка \(N\) - середина \(B C\).
б) Так как объём призмы равен 12, а её высота равна 2, площадь параллелограмма \(A B C D\) = 6.
Прямоугольные треугольники \(A F M\) и \(N E K\) равны по катету и гипотенузе, значит, \(A F=E N\).
Тогда \(A B N\) равнобедренный треугольник с основанием \(A N=3\).
Площадь этого треугольника равна 1,5 .
Значит, его высота \(h\), проведённая из вершины \(B\), равна 1 , а высота трапеции \(A M K N\) равна
\(\sqrt{B B_1^2+\left(\frac{h}{3}\right)^2}=\dfrac{\sqrt{37}}{3}\).
Средняя линия трапеции равна \(\dfrac{5}{2}\), а значит, её площадь равна \(\dfrac{5 \sqrt{37}}{6}\).
Ответ
(ЕГЭ, 2023) В правильной треугольной призме \(A B C A_1 B_1 C_1\) точка \(M\) является серединой ребра \(B B_1\), а точка \(N\) - середина ребра \(A_1 C_1\). Плоскость \(\alpha\), параллельная прямым \(A M\) и \(B_1 N\), проходит через середину отрезка \(M N\).
а) Докажите, что плоскость \(\alpha\) проходит через середину отрезка \(B_1 M\).
б) Найдите площадь сечения призмы \(A B C A_1 B_1 C_1\) плоскостью \(\alpha\), если все рёбра призмы имеют длину 4.
Решение
a) Пусть точка \(P\) - середина отрезка \(M N\), а точка \(Q\) - середина отрезка \(B_1 M\)
Тогда отрезок \(P Q\) - средняя линия треугольника \(M N B_1\), параллельная стороне \(B_1 N\).
Значит, отрезок \(P Q\) принадлежит плоскости \(\alpha\). Следовательно, плоскость \(\alpha\) проходит через середину \(Q\) отрезка \(B_1 M\)
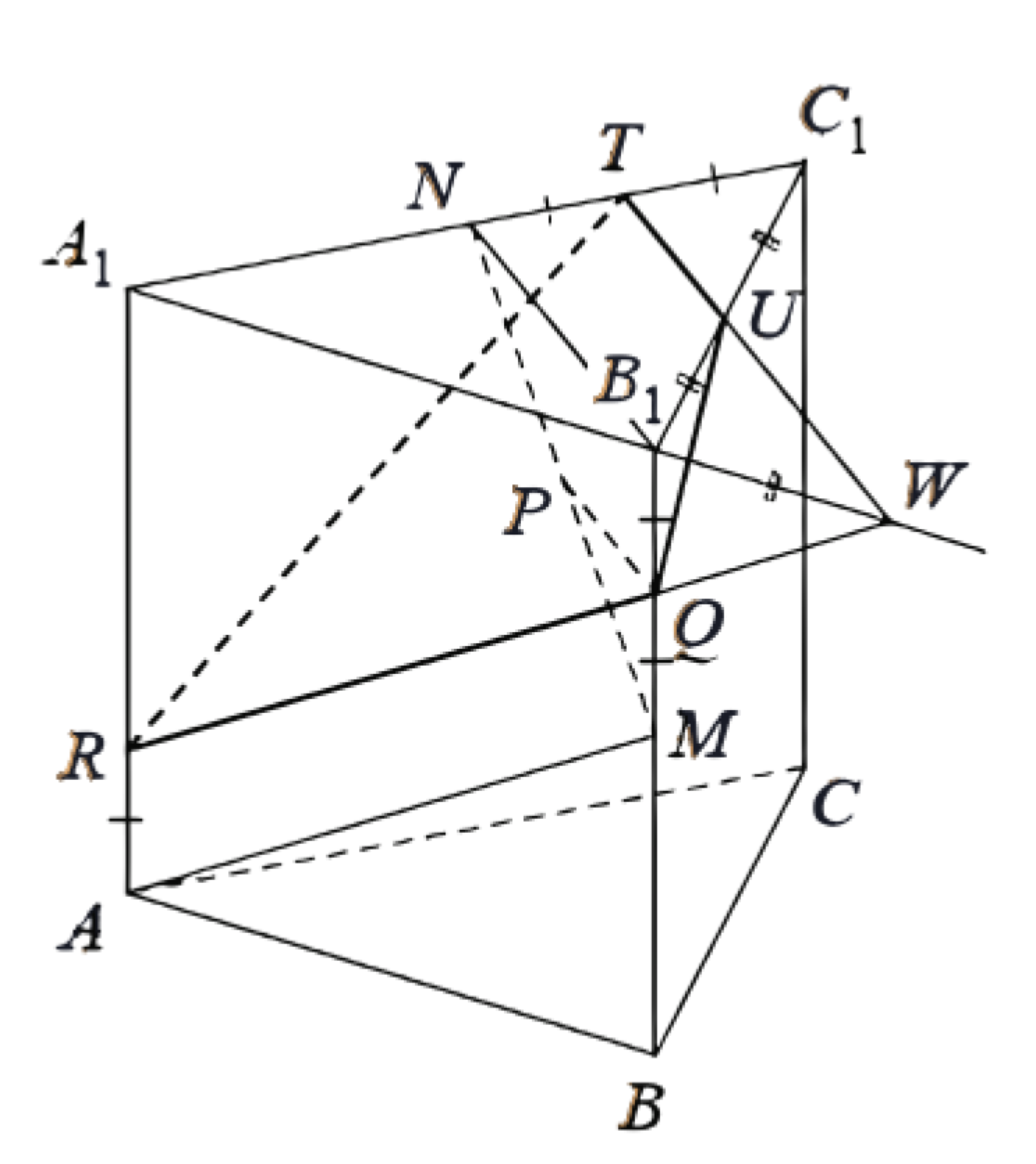
б) Обозначим точки пересечения плоскости \(\alpha\) с прямыми \(A A_1, A_1 B_1, B_1 C_1\) и \(A_1 C_1\) через \(R\), \(W, U\) и \(T\) соответственно. Тогда точки \(R, Q\) и \(W\) лежат на одной прямой, параллельной прямой
\(A M\), а точки \(W, U\) и \(T\) лежат на одной прямой, параллельной прямой \(B_1 N\), поскольку плоскость \(\alpha\) параллельна прямым \(A M\) и \(B_1 N\). Сечением призмы \(\ A B C A_1 B_1 C_1\) плоскостью \(\alpha \) является
четырёхугольник \(R T U Q\).
Четырёхугольник \(A R Q M\) - параллелограмм, следовательно:
\(A R=Q M=\dfrac{1}{2} B_1 M=\dfrac{1}{4} B B_1=1 ; A_1 R=3\)
Треугольники \(R A_1 W\) и \(Q B_1 W\) подобны, поэтому:
\(A_1 W: B_1 W=A_1 R: B_1 Q=3: 1 ; A_1 W=6\) .
Прямые \(B_1 N\) и \(T W\) параллельны, поэтому:
\(A_1 N: N T=A_1 B_1: B_1 W=2: 1\);
\(T C_1=N T=\dfrac{1}{2} A_1 N=1\);
\(B_1 U: U C_1=N T: T C_1=1: 1\);
\(B_1 U=U C_1=2 ; T W=\dfrac{3}{2} N B_1=3 \sqrt{3}\) .
В прямоугольном треугольнике \(R A_1 T\) находим:
\(R T=\sqrt{R A_1^2+A_1 T^2}=\sqrt{3^2+3^2}=3 \sqrt{2}\).
В прямоугольном треугольнике \(R A_1 W\) находим:
\(R W=\sqrt{R A_1^2+A_1 W^2}=\sqrt{3^2+6^2}=3 \sqrt{5}\) .
Поскольку \(\ R W^2=R T^2+T W^2\), треугольник \(R T W\) прямоугольный, и его площадь равна \(\dfrac{1}{2} R T \cdot T W=\dfrac{9 \sqrt{6}}{2}\) .
Поскольку \(\quad \dfrac{W U}{W T}=\dfrac{2}{3}, \quad \dfrac{W Q}{W R}=\dfrac{1}{3}, \quad\) площадь \(\quad\) треугольника \(\quad Q U W\) составляет \(\ \dfrac{2}{3} \cdot \dfrac{1}{3}=\dfrac{2}{9}\)
от площади треугольника \(R T W\). Площадь сечения \(R T U Q\) равна разности площадей треугольников \(R T W\) и \(Q U W\). Значит, эта площадь равна
\begin{equation*}
\frac{7}{9} \cdot \dfrac{9 \sqrt{6}}{2}=\dfrac{7 \sqrt{6}}{2}
\end{equation*}
Ответ
(ЕГЭ, 2023) Грани \(A B D\) и \(A C D\) тетраэдра \(A B C D\) являются правильными треугольниками со стороной 4 и перпендикулярны друг другу. Плоскость \(\alpha\) перпендикулярна ребру \(C D\) и пересекает рёбра \(A B\) и \(C D\) в точках \(K\) и \(M\) соответственно, причём \(C M: M D=5: 3\).
a) Докажите, что \(K\) - середина ребра \(A B\).
б) Найдите площадь сечения тетраэдра плоскостью \(\alpha\).
Решение
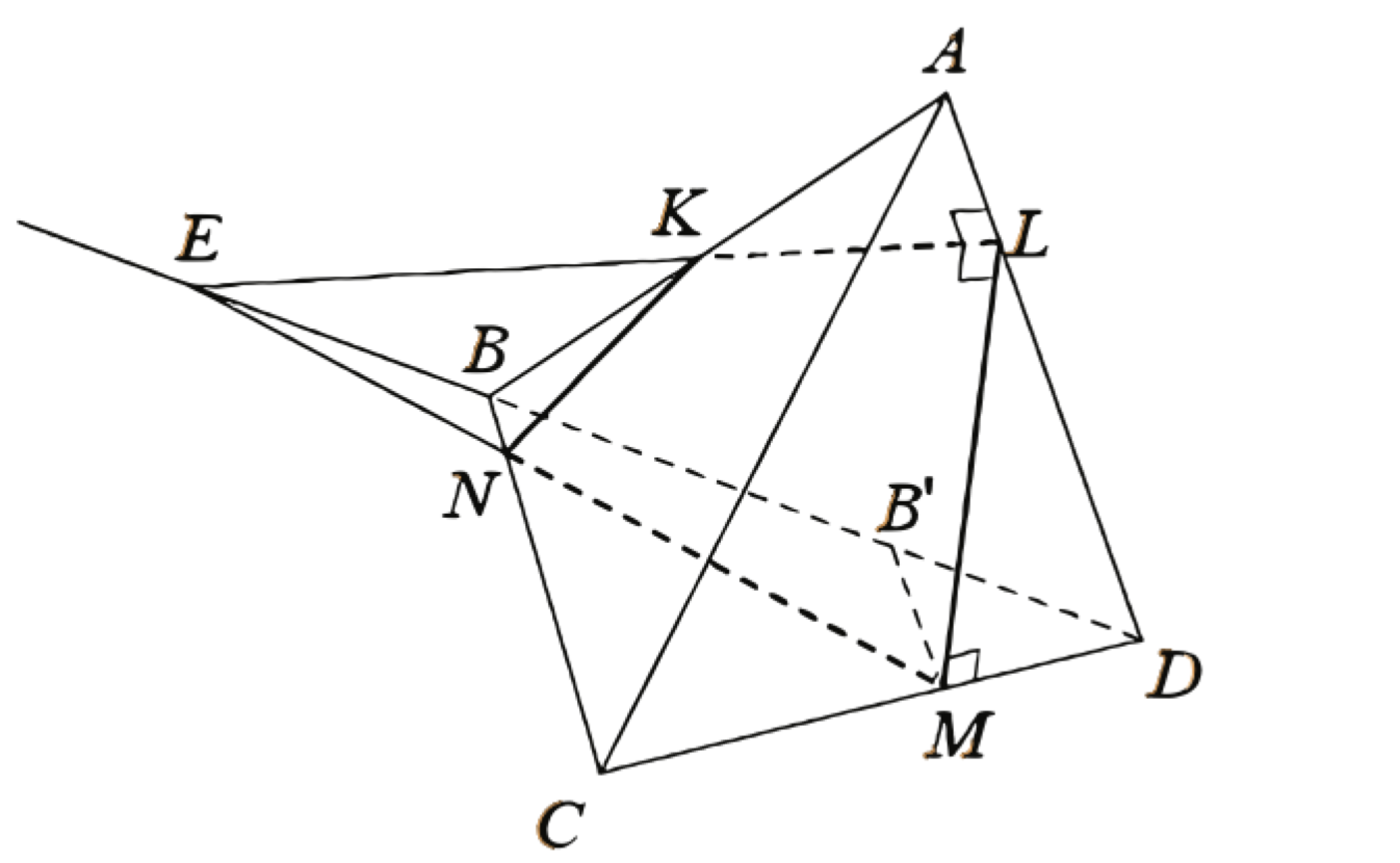
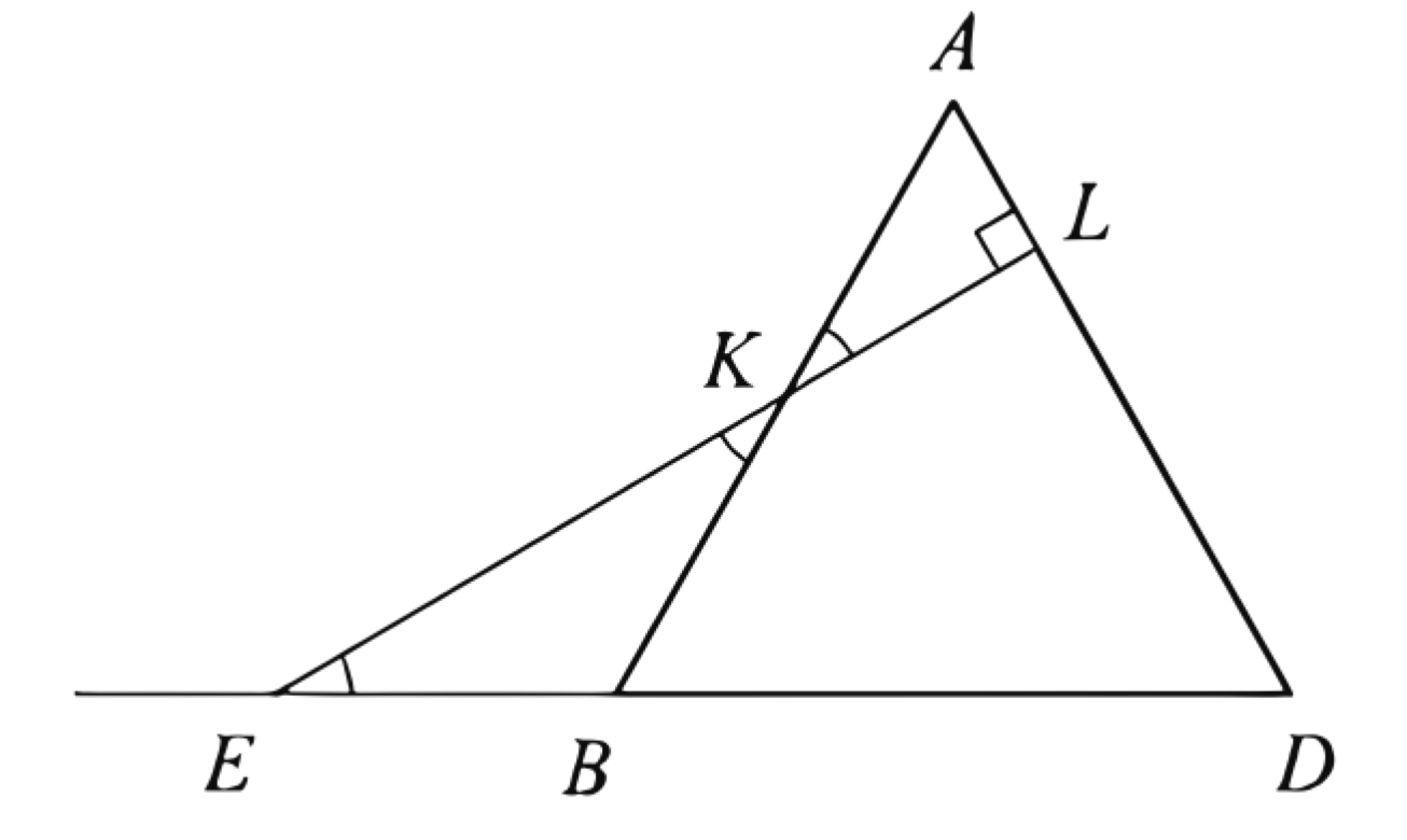
a) Пусть \(L\) - точка на ребре \(A D\) такая, что отрезок \(M L\) перпендикулярен ребру \(C D\) (рис. 1).
Тогда точка \(L\) принадлежит плоскости \(\alpha\).
В прямоугольном треугольнике \(M L D\) угол \(D\) = \(60^{\circ}\),
поэтому \(L D=2 M D=2 \cdot \dfrac{3}{8} C D=2 \cdot 1,5=3\) .
Плоскости \(\alpha\) и \(A B D\) перпендикулярны плоскости \(A C D\). Следовательно, прямая \(K L\) перпендикулярна плоскости \(A C D\). В прямоугольном треугольнике \(L K A\) угол \(A\) равен \(60^{\circ}\), поэтому \(K A=2 L A=2 \cdot(A D-L D)=2\) .
Значит, точка \(K\) - середина \(A B\).
б) Из прямоугольных треугольников
\(M L D\) и \(L K A\) имеем: \(M L=\dfrac{3 \sqrt{3}}{2}\),
\(L K=\sqrt{3}\).
Пусть прямые \(L K\) и \(B D\) пересекаются в точке \(E\) (рис.2), а прямые \(E M\) и \(B C\) пересекаются в точке \(N\). Треугольник \(E B K\) равнобедренный с углом \(120^{\circ}\) при вершине \(B\), поэтому
\(E B=B K=2\) и \(E K=2 \sqrt{3}\). Рассмотрим точку \(B^{\prime}\) на ребре \(B D\) такую, что прямые \(B N\) и \(B^{\prime} M\) параллельны. Тогда \(B B^{\prime}: B^{\prime} D=C M: M D=5: 3\).
Следовательно, \(E N: N M=E B: B B^{\prime}=4: 5 \text {. }\)
Поскольку \(\dfrac{E K}{E L}=\dfrac{2}{3} \quad\) и \( \dfrac{E N}{E M}=\dfrac{4}{9}\), площадь треугольника \(E K N\) составляет \(\dfrac{2}{3} \cdot \dfrac{4}{9}=\dfrac{8}{27}\) от площади треугольника \(E L M\).
Площадь прямоугольного треугольника \(E L M\) равна \(\dfrac{1}{2} \cdot E L \cdot L M=\dfrac{1}{2} \cdot 3 \sqrt{3} \cdot \dfrac{3 \sqrt{3}}{2}=\dfrac{27}{4}\).
Площадь сечения \(K L M N\) равна разности площадей треугольников \(E L M\) и \(E K N\). Значит, эта площадь равна \(\dfrac{19}{27} \cdot \dfrac{27}{4}=\dfrac{19}{4} \text {. }\)
Ответ
(ЕГЭ, 2023) На рёбрах \(A C, A D, B D\) и \(B C\) тетраэдра \(A B C D\) отмечены точки \(K, L, M\) и \(N\) соответственно, причём \(A K: K C=3: 7\). Четырёхугольник \(K L M N-\) квадрат со стороной 3.
a) Докажите, что \(B M: M D=3: 7\).
б) Найдите расстояние от вершины \(C\) до плоскости \(K L M\), если объём тетраэдра \(A B C D\) равен 50.
Решение
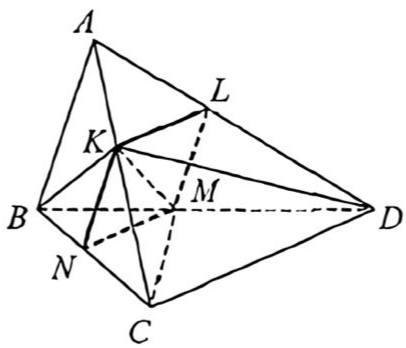
a) Плоскость \(B C D\) параллельна прямой \(K L\), поскольку содержит параллельную ей прямую \(M N\) (рис.1).
Следовательно, прямые \(K L\) и \(C D\) параллельны. Аналогично прямые \(L M\) и \(A B\) параллельны, а значит, \(B M: M D=A L: L D=A K: K C=3: 7 \text {. }\)
б) Обозначим искомое расстояние от точки \(C\) до плоскости \(K L M\) через \(x\). Тогда объём пирамиды
\(C K M N\) равен \(V_{C K M N}=\dfrac{1}{3} \cdot x \cdot \dfrac{K N \cdot N M}{2}=\dfrac{3}{2} x \).
Найдём объём пирамиды \(C K M N\) другим способом. Пусть \(h\) - высота пирамиды \(A B C D\), проведённая из вершины \(A\). Тогда высота пирамиды \(K B C D\), проведённая из вершины \(K\), равна
\(\quad \dfrac{7}{10} h, \) поскольку \(K C: A C=7: 10\).
Следовательно, объём пирамиды \(K B C D\) равен 35 .
Пирамиды \(K B C D\) и \(C K M N\) имеют общую высоту, проведённую из вершины \(K\).
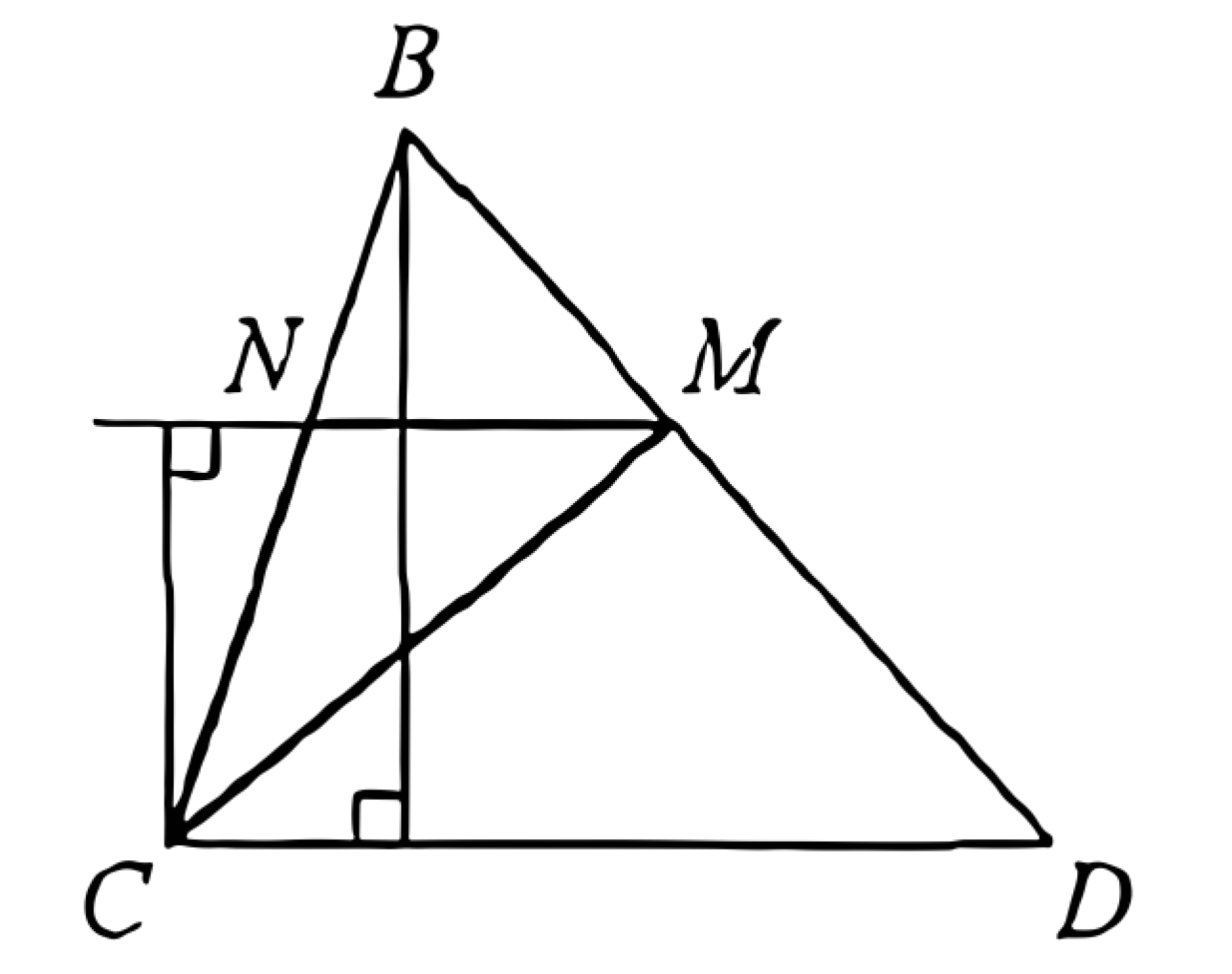
Сравним площади треугольников \(C N M\) и \(B C D\) (рис.2). Высоты этих треугольников, проведённые из вершин \(C\) и \(B\) соответственно, относятся как \(C N: B C=C K: A C=7: 10,\)
а их стороны \(N M\) и \(C D\) относятся как \(N M: C D=B M: B D=3: 10,\)
поскольку треугольники \(B N M\) и \(B C D\) подобны. Следовательно, отношение площадей треугольников \(C N M\) и \(B C D\) равно \(\dfrac{21}{100}\). Значит, объём пирамиды CKMN равен \(\dfrac{21}{100} \cdot 35=\dfrac{147}{20}\),
откуда получаем: \(\dfrac{3}{2} x=\dfrac{147}{20} ; x=4,9\).
Ответ
(ЕГЭ, 2023) В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит равнобедренная трапеция \(A B C D\) с основаниями \(A D=5\) и \(B C=3\). Точка \(M\) делит ребро \(A_1 D_1\) в отношении \(A_1 M: M D_1=2: 3\), а точка \(K\) - середина ребра \(D D_1\).
a) Докажите, что плоскость \(M K C\) параллельна прямой \(B D\).
б) Найдите тангенс угла между плоскостью \(M K C\) и плоскостью основания призмы, если \(\angle M K C=90^{\circ}, \angle A D C=60^{\circ}\).
Решение
a) Боковая грань \(B C C_1 B_1\) призмы параллельна грани \(A D D_1 A_1\), поскольку составляющие их рёбра соответственно параллельны. Проведём через вершину \(C\) прямую, параллельную \(K M\).
Пусть эта прямая пересекает ребро \(B B_1\) в точке \(N\) (см. рисунок).
Прямоугольные треугольники
\(C B N\) и \(M D_1 K\) равны, поскольку равны их катеты \(B C\) и \(M D_1\), а также острые углы ввиду параллельности соответствующих сторон. Следовательно, \(B N=D_1 K=\dfrac{1}{2} D D_1=\dfrac{1}{2} B B_1\), а
значит, точка \(N\) - середина ребра \(B B_1\). Значит, \(B N K D-\) параллелограмм, а прямая \(N K\), лежащая в плоскости \(M K C\), параллельна прямой \(B D\). Таким образом, плоскость \(M K C\) параллельна \(B D\).
б) Пусть высота призмы равна \(2 x\).
Тогда \(B_1 N=B N=D K=x\).
В равнобедренной трапеции с основаниями 5 и 3 и углом \(60^{\circ}\) боковые стороны равны 2 , то есть
\(A B=C D=2\).
Из прямоугольных треугольников \(C B N, C D K\) и \(N C K\) имеем:
\(N C^2=B N^2+B C^2=x^2+9, C K^2=\)
\(=C D^2+D K^2=x^2+4\);
\(N K^2=N C^2+C K^2=x^2+9+x^2+4=\)
\(=2 x^2+13\).
Для треугольника \(B C D\) имеем:
\(B D^2=B C^2+C D^2-2 B C \cdot C D \cdot \cos 120^{\circ}=19\)
Поскольку \(N K=B D\), получаем: \(2 x^2+13=19\), откуда \(x=\sqrt{3}\).
При пересечении плоскостей
\(M K C\) и \(B C D\) плоскостью \(B D D_1\) получены параллельные прямые \(B D\) и \(N K\). Следовательно, прямая пересечения плоскостей \(M K C\) и \(B C D\) параллельна прямой \(B D\) и проходит через точку \(C\).
Плоскость, проходящая через точку \(C\) перпендикулярно прямой \(B D\), в пересечении с плоскостями \(B C D\) и \(M K C\) образует линейный угол двугранного угла, образованного этими плоскостями.
Тангенс угла между плоскостью \(M K C\) и плоскостью \(B C D\) равен отношению расстояния от прямой \(N K\) до плоскости \(B C D\), то есть \(x\), и высоты \(h\) треугольника \(B C D\), проведённой из вершины \(C\).
Площадь треугольника \(B C D\) равна \(\dfrac{h \cdot B D}{2}=\dfrac{h \sqrt{19}}{2}\).
С другой стороны, эта площадь
равна \(\dfrac{B C \cdot C D \cdot \sin \angle B C D}{2}=\dfrac{3 \sqrt{3}}{2}\) .
Следовательно, \(h=\dfrac{3 \sqrt{57}}{19}\), а значит, искомый тангенс равен
\(\dfrac{x}{h}=\dfrac{\sqrt{19}}{3} \text {. }\)
Ответ
(ЕГЭ, 2023) В основании прямой призмы \(A B C A_1 B_1 C_1\) лежит равнобедренный треугольник \(A B C\) с основанием \(A B\). Точка \(P\) делит ребро \(A B\) в отношении \(A P: P B=1: 3\), а точка \(Q\) - середина ребра \(A_1 C_1\). Через середину \(M\) ребра \(B C\) провели плоскость \(\alpha\), перпендикулярную отрезку \(P Q\).
а) Докажите, что плоскость \(\alpha\) делит ребро \(A C\) пополам.
б) Найдите отношение, в котором плоскость \(\alpha\) делит ребро \(A_1 C_1\), считая от точки \(A_1\), если
известно, что \(A B=A A_1, A B: B C=2: 5\)
Решение
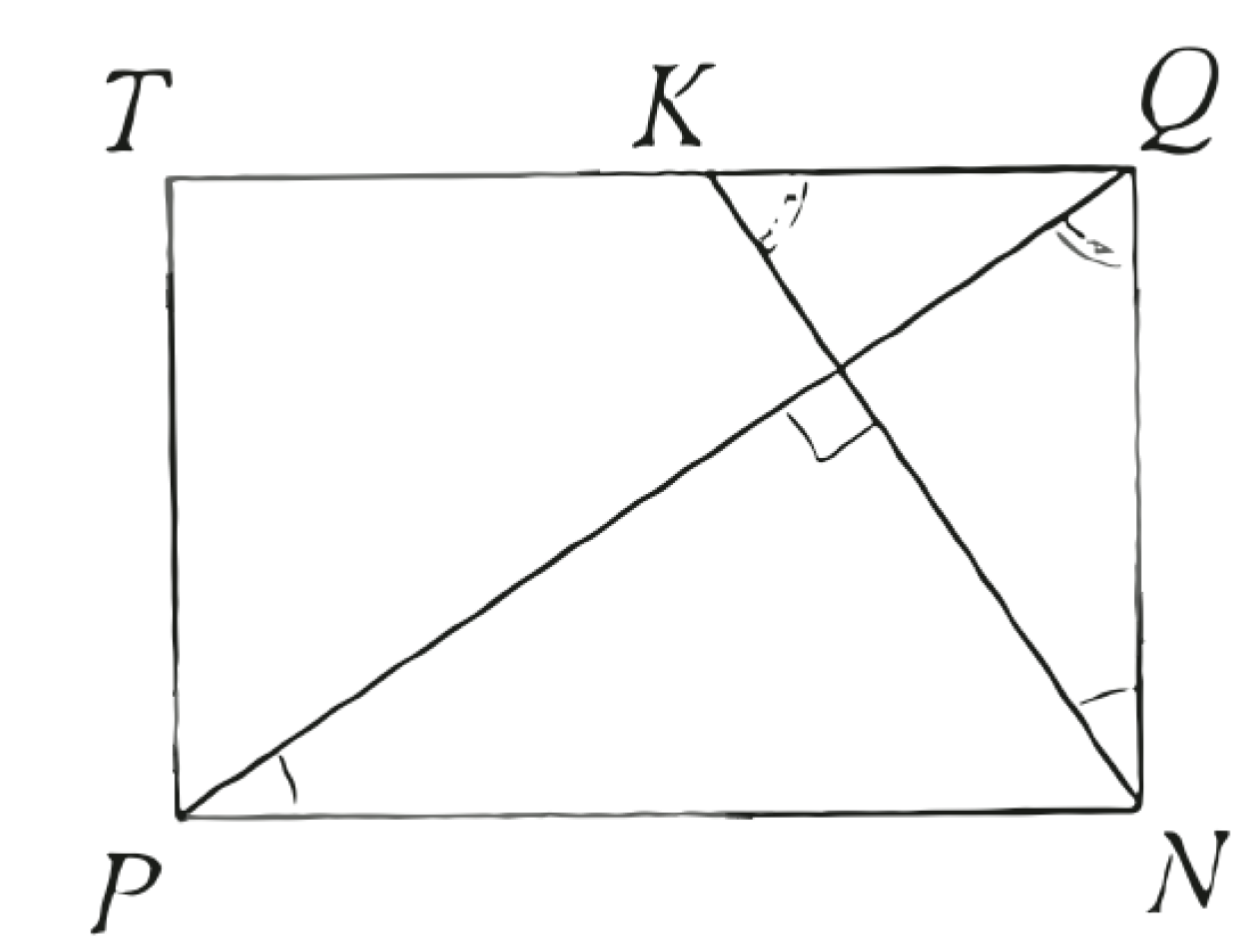
a) Пусть точка \(N\) - середина ребра \(A C\) (рис.1). Тогда отрезки \(M N\) и \(Q N\) перпендикулярны, поскольку отрезок \(Q N\) является высотой призмы. Отрезки \(M N\) и \(P N\) также перпендикулярны, поскольку отрезок \(P N\) параллелен высоте равнобедренного треугольника \(A B C\), проведённой из вершины \(C\), а эта высота перпендикулярна средней линии \(M N\).
Таким образом, отрезок \(M N\) перпендикулярен плоскости \(P Q N\), а значит, и отрезку \(P Q\).
Следовательно, плоскость \(\alpha\) проходит через середину \(N\) ребра \(A C\).
б) Пусть \(A B=A A_1=2 a\), тогда: \(A C=B C=5 a ; A N=\dfrac{A C}{2}=\dfrac{5 a}{2}\).
Из прямоугольного треугольника \(A P N\) имеем: \(P N=\sqrt{A N^2-A P^2}=\sqrt{\dfrac{25 a^2}{4}-\dfrac{a^2}{4}}=\)
\(=\sqrt{6} \cdot a\).
Пусть отрезок \(P T\) - высота призмы, а плоскость \(\alpha\) пересекает ребро \(A_1 C_1\) и прямую \(Q T\) в точках \(L\) и \(K\) соответственно. Тогда прямая \(N K\) перпендикулярна отрезку \(P Q\), а прямая \(K L\) параллельна прямой \(A_1 B_1\).
В прямоугольнике \(P T Q N\) имеем: \(Q N=A A_1=2 a\), \(T Q=P N=\sqrt{6} \cdot a\) (рис. 2).
Прямоугольные треугольники \(P Q N\) и \(N K Q\) подобны, поскольку
\(\angle P Q N=90^{\circ}-\angle K N Q=\angle N K Q \text {. }\)
Следовательно, \(\dfrac{K Q}{Q N}=\dfrac{Q N}{N P} ; K Q=\dfrac{Q N^2}{N P}=\dfrac{4 a^2}{\sqrt{6} \cdot a}=\)
\(=\dfrac{2 \sqrt{6} \cdot a}{3} ; T K=\dfrac{\sqrt{6} \cdot a}{3}\).
Прямые \(K L\) и \(A_1 B_1\) параллельны. Следовательно,
\(A_1 L: A_1 Q=T K: T Q=\)
\(=\left(\dfrac{\sqrt{6} \cdot a}{3}\right):(\sqrt{6} \cdot a)=1: 3 \).
Значит, \(A_1 L: A_1 C_1=A_1 L:\left(2 A_1 Q\right)=1: 6 ;\)
\(A_1 L: L C_1=1: 5\).