Чтобы получить дополнительный функционал нужно войти.
(ЕГЭ,2017) Две окружности касаются внутренним образом в точке , причём меньшая окружность проходит через центр большей. Диаметр большей окружности вторично пересекает меньшую окружность в точке , отличной от . Лучи и вторично пересекают большую окружность в точках и соответственно. Точка лежит на дуге большей окружности, не содержащей точку .
a) Докажите, что прямые и параллельны.
б) Известно, что . Прямые и пересекаются в точке . Найдите отношение .
(ЕГЭ,2017) Окружность, вписанная в трапецию , касается её боковых сторон и в точках и соответственно. Известно, что и .
a) Докажите, что .
б) Найдите длину отрезка , если радиус окружности равен .
(ЕГЭ,2017) В треугольник , в котором длина стороны меныше длины стороны , вписана окружность с центром . Точка симметрична точке относительно прямой .
a) Докажите, что точки и лежат на одной окружности.
б) Найдите площадь четырёхугольника , если и .
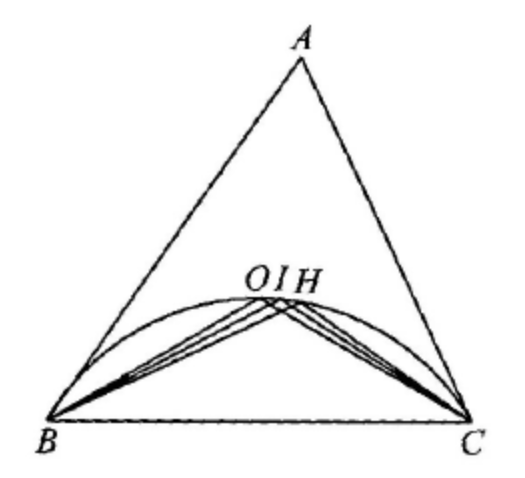
(ЕГЭ,2016) Точка - центр окружности, описанной около остроугольного треугольника - центр вписанной в него окружности, - точка пересечения высот. Известно, что .
a) Докажите, что точка лежит на окружности, описанной около треугольника .
б) Найдите угол , если .
Решение
a) Точка - центр описанной окружности около треугольника , поэтому .
Значит,
откуда
Найдём утол :
Значит, , поэтому точки и лежат на одной окружности.
б) Найдём угол :
Значит, , поэтому точки и лежат на одной окружности.
Поскольку , получаем . В равнобедренном треугольнике имеем .
Поскольку прямая перпендикулярна , получаем
Значит, .
Биссектриса угла треугольника лежит внутри угла, образованного медианой и высотой, исходящими из той же вершины, поэтому лучи и пересекают дугу окружности в указанном на рисунке порядке. Четырёхугольник вписан в окружность, поэтому
Ответ
б)
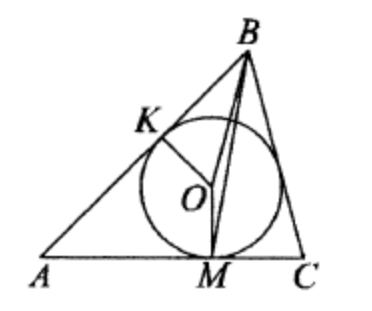
(ЕГЭ,2016) В треугольнике угол равен . Окружность, вписанная в треугольник, касается стороны в точке .
a) Докажите, что отрезок не болыше утроенного радиуса вписанной в треугольник окружности.
б) Найдите , если известно, что отрезок в 2,5 раза больше радиуса вписанной в треугольник окружности.
Решение
a) Пусть - центр вписанной в треугольник окружности, - её радиус, а - точка касания со стороной . Тогда , поскольку точка лежит на биссектрисе угла .
Значит,
Имеем: .
б) Заметим, что . В треугольнике имеем:
По теореме косинусов получаем:
откуда .
Ответ
б)
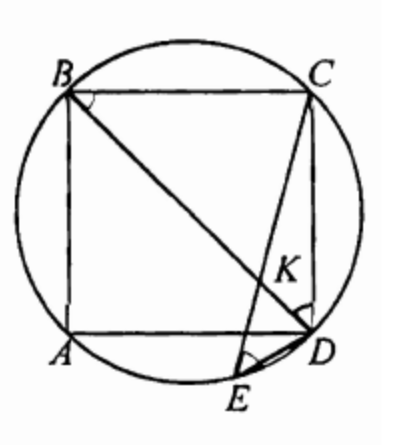
(ЕГЭ,2016) Квадрат вписан в окружность. Хорда пересекает его диагональ в точке .
a) Докажите, что .
б) Найдите отношение и , если
Решение
а) В треугольниках и угол - общий,
Значит, эти треугольники подобны, откуда
б) В треугольнике имеем:
откуда .
Из подобия треугольников и получаем:
В треугольнике имеем:
то есть
откуда
Ответ
б) 2:1
