a) Поскольку точка \(O-\) центр вписанной в треугольник \(A B C\) окружности, лучи \(B O\) и \(C O\) являются биссектрисами углов треугольника \(A B C\). Угол \(P O C\) является внешним углом треугольника \(B O C\).

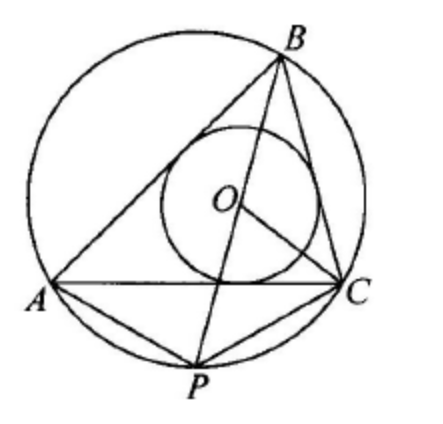
Следовательно,
\begin{equation*}
\angle P O C=\angle B C O+\angle C B O=\frac{1}{2} \angle A C B+\frac{1}{2} \angle A B C .
\end{equation*}

Углы \(A C P\) и \(A B P\) равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника \(A B C\), поэтому \begin{equation*}
\angle P C O=\angle A C P+\angle A C O=\angle A B P+\angle A C O=\frac{1}{2} \angle A B C+\frac{1}{2} \angle A C B .
\end{equation*}

Таким образом, \(\angle P O C=\angle P C O\).

б) Пусть \(R=8\) - радиус окружности, описанной около треугольника \(A B C\). Хорды \(A P\) и CP стягивают равные дуги окружности, описанной около треугольника \(A B C\), поэтому
\begin{equation*}
C P=A P=2 R \sin \angle A B P=2 R \sin 30^{\circ}=8 .
\end{equation*}

Таким образом, площадь треугольника \(A P C\) равна
\begin{equation*}
\frac{A P \cdot C P \cdot \sin \angle A P C}{2}=\frac{A P^2 \cdot \sin \left(180^{\circ}-\angle A B C\right)}{2}=\frac{A P^2 \cdot \sin 120^{\circ}}{2}=16 \sqrt{3} .
\end{equation*}

a) Точки \(M\) и \(N\) лежат на окружности диаметром \(B C\), поэтому \(\angle A N M=180^{\circ}-\angle M N C=\angle A B C\).

Значит, треугольники \(A N M\) и \(A B C\) подобны с коэффициентом подобия \(\frac{A M}{A C}=\cos \angle B A C=\cos 60^{\circ}=\frac{1}{2} . \quad\) Следовательно, радиус окружности, описанной около треугольника \(A N M\), равен \(\frac{1}{2} A O\).

Точки \(M\) и \(N\) лежат на окружности диаметром \(A H\), поэтому \(A H=A O\).

б) Пусть прямые \(A H\) и \(B C\) пересекаются в точке \(K\), а точка \(L\) - середина стороны \(A C\), тогда
\begin{equation*}
\angle A K B=90^{\circ}, \angle A O L=\frac{1}{2} \angle A O C=\frac{1}{2} \cdot 2 \angle A B C=\angle A B C=45^{\circ} .
\end{equation*}

Значит,
\begin{equation*}
\begin{gathered}
\angle O A L=90^{\circ}-\angle A O L=45^{\circ}, \angle B A K=90^{\circ}-\angle A B C=45^{\circ} ; \\
\angle O A H=\angle B A K+\angle O A L-\angle B A C=30^{\circ} .
\end{gathered}
\end{equation*}

Площадь треугольника \(A H O\) равна
\begin{equation*}
\frac{A O \cdot A H \cdot \sin \angle O A H}{2}=\frac{A O^2 \cdot \sin 30^{\circ}}{2}=\frac{B C^2 \cdot \sin 30^{\circ}}{8 \sin ^2 60^{\circ}}=9 \text {. }
\end{equation*}

a) Заметим, что \(\angle A C H=90^{\circ}-\angle C A B=\angle A B C\).

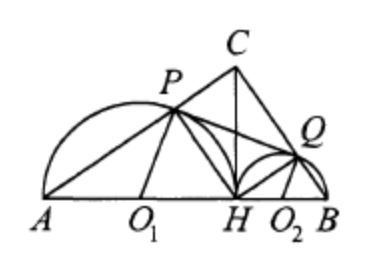
Отношение площадей кругов, построенных на отрезках \(A H\) и \(B H\), равно квадрату отношения их диаметров:
\begin{equation*}
\begin{aligned}
& \left(\frac{A H}{B H}\right)^2=\left(\frac{A H \cdot C H}{B H \cdot C H}\right)^2=\left(\frac{A H}{C H} \cdot \frac{C H}{B H}\right)^2= \\
& =(\operatorname{tg} \angle A C H \cdot \operatorname{tg} \angle A B C)^2=(\operatorname{tg} \angle A B C)^4 .
\end{aligned}
\end{equation*}

б) Точки \(P\) и \(Q\) лежат на окружностях диаметрами \(A H\) и \(B H\) соответственно, значит, \(\angle A P H=\angle H Q B=90^{\circ}\).
Следовательно, четырёхугольник \(P C Q H\) - прямоугольник. Значит, площадь \(S_{P Q H}\) треугольника \(P Q H\) равна половине площади \(S_{C P H Q}\) прямоугольника \(C P H Q\). Поскольку \(P O_1\) и \(Q O_2\) являются медианами треугольников \(A P H\) и \(H Q B\) соответственно, площадь \(S_{O_1 P H}\) треугольника \(O_1 P H\) равна половине площади \(S_{A P H}\) треугольника \(A P H\), а площадь \(S_{\mathrm{O}_2 Q H}\) треугольника \(\mathrm{O}_2 \mathrm{QH}\) равна половине площади \(S_{H Q B}\) треугольника \(H Q B\).
Следовательно, площадь четырёхугольника \(O_1 P Q O_2\) равна
\begin{equation*}
S_{O_1 P H}+S_{P Q H}+S_{O_2 Q H}=\frac{1}{2} S_{A P H}+\frac{1}{2} S_{C P H Q}+\frac{1}{2} S_{H Q B}=\frac{1}{2} S_{A B C}=\frac{A C \cdot B C}{4}=30 .
\end{equation*}