17. Планиметрия

226

(ЕГЭ,2020) Две окружности касаются внутренним образом в точке .
Вершины и равнобедренного прямоугольного треугольника с прямым углом лежат большей и меньшей окружностях соответственно.
Прямая вторично пересекает меньшую окружность в точке .
Прямая вторично пересекает большую окружность в точке .

a) Докажите, что параллельно .

б) Найдите , если радиусы окружностей равны и .

Решение

a) и диаметры меньшей и большей окружностей соответственно

- равнобедренный,
- равнобедренный, , а это соответственные углы при прямых и и секущей . Следовательно, .

б) по двум углам и ;
по условию , откуда . .

Ответ

б)

227

(ЕГЭ,2020) Биссектриса прямого угла прямоугольного треугольника вторично пересекает окружность, описанную около этого треугольника, в точке . Прямая, проходящая через точку и середину гипотенузы , пересекает катет в точке .

a) Докажите, что .

б) Найдите площадь треугольника , если и .

Решение

a) Поскольку луч - биссектриса угла , дуги и равны, а значит, стягивающие их соответственные одноимённые хорды равны.

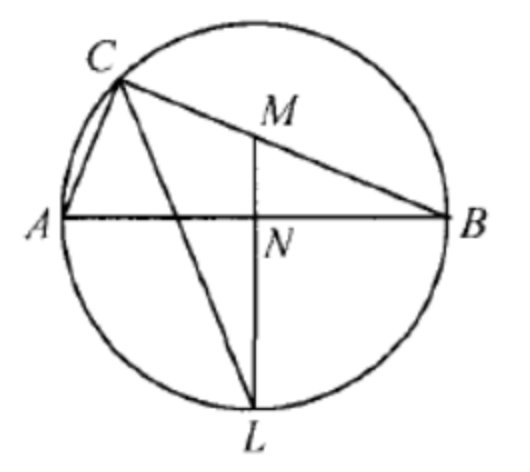
Следовательно, треугольник равнобедренный, а прямая - серединный перпендикуляр к отрезку . Прямоугольные треугольники и имеют общий угол . Значит, они подобны, откуда получаем, что .

б) Пусть , тогда из подобия треугольников и получаем:

откуда или .
Условию задачи удовлетворяет . Получаем, что

Площадь треугольника равна

Ответ

б) 80

228

ЕГЭ,2019) Дана трапеция с основаниями и . Точки и - середины сторон и соответственно. Окружность проходит через точки и и пересекает отрезки и в точках и , отличных от концов отрезков, соответственно.

a) Докажите, что точки и лежат на одной окружности.

б) Найдите , если отрезки и перпендикулярны, , .

Решение

a) Четырёхугольник вписан в окружность, а средняя линия трапеции параллельна её основанию , значит,

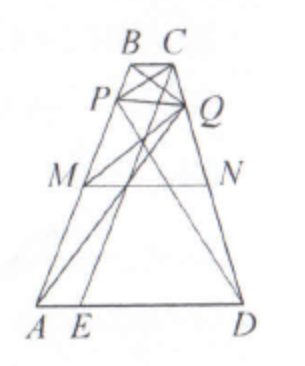
Таким образом, сумма противоположных углов четырёхугольника равна , значит, около него можно описать окружность.

б) В четырёхугольнике :

значит, около четырёхугольника можно описать окружность.
По свойству вписанных углов

Таким образом, треугольник прямоугольный, а значит, .
Средняя линия трапеции следовательно, треугольник равнобедренный, а .
Пусть прямая, параллельная прямой , проходит через точку и пересекает основание в точке . Тогда в треугольнике :

Поскольку средняя линия трапеции параллельна её основаниям, , откуда получаем:

Ответ

б)

229

(ЕГЭ,2019) Две окружности разных радиусов касаются внешним образом в точке . Прямая касается первой окружности в точке , а второй окружности в точке . Луч пересекает первую окружность в точке , луч пересекает вторую окружность в точке .

a) Докажите, что четырёхугольник - трапеция.

б) Найдите радиус окружности, описанной около треугольника , если радиус первой окружности равен , а радиус второй окружности равен .

Решение

a) Пусть прямая $К М$ - общая касательная двух окружностей, причём точка лежит на отрезке .

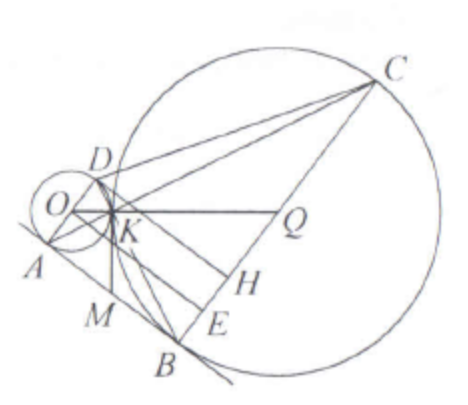
Тогда по свойству отрезков касательных, проведённых из одной точки к окружности, . Следовательно, точка лежит на окружности диаметром , а значит, .
Углы и прямые, поэтому и - диаметры первой и второй окружностей соответственно. Значит, неравные отрезки и перпендикулярны касательной , следовательно, они параллельны. Таким образом, четырёхугольник - трапеция.

б) Пусть точки и - центры первой и второй окружностей соответетвенно, а точки и - проекции точек и соответственно на прямую . Тогда в прямоугольном треугольнике :

В прямоугольном треугольнике :

По теореме синусов радиус окружности, описанной около треугольника , равен

Ответ

б)

230

(ЕГЭ,2019) Точка - центр вписанной в треугольник окружности. Прямая вторично пересекает описанную около этого треугольника окружность в точке .

a) Докажите, что .

б) Найдите площадь треугольника , если радиус описанной около треугольника окружности равен .

Решение

a) Поскольку точка - центр вписанной в треугольник окружности, лучи и являются биссектрисами углов треугольника . Угол является внешним углом треугольника .

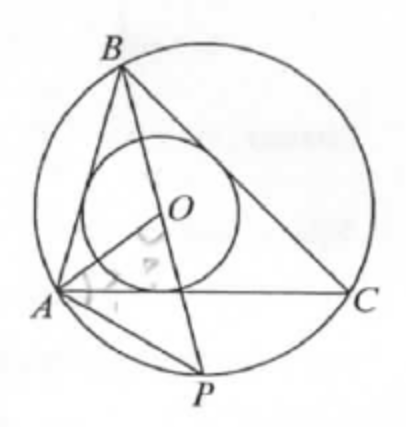
Следовательно,

Углы и равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника , поэтому

Таким образом, .
б) Пусть - радиус окружности, описанной около треугольника .

Поскольку , треугольник равнобедренный, следовательно,

Таким образом, площадь треугольника равна

Ответ

б)

231

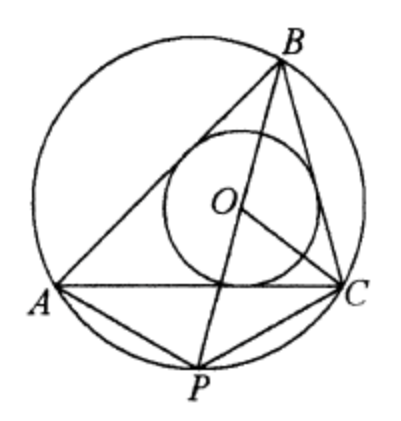
(ЕГЭ,2019) Точка - центр вписанной в треугольник окружности. Прямая вторично пересекает описанную около этого треугольника окружность в точке .

a) Докажите, что .

б) Найдите радиус описанной около треугольника окружности, если расстояние от точки до прямой равно .

Решение

a) Поскольку точка - центр вписанной в треугольник окружности, лучи и являются биссектрисами углов треугольника . Угол является внешним углом треугольника .

Следовательно,

Углы и равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника , поэтому

Таким образом, . Следовательно, треугольник равнобедренный, то есть .
б) Пусть - радиус окружности, описанной около треугольника .

По теореме синусов

Тогда расстояние от точки до прямой равно

Получаем: , откуда .

Ответ

б) 36