17. Планиметрия
Чтобы получить дополнительный функционал нужно войти.
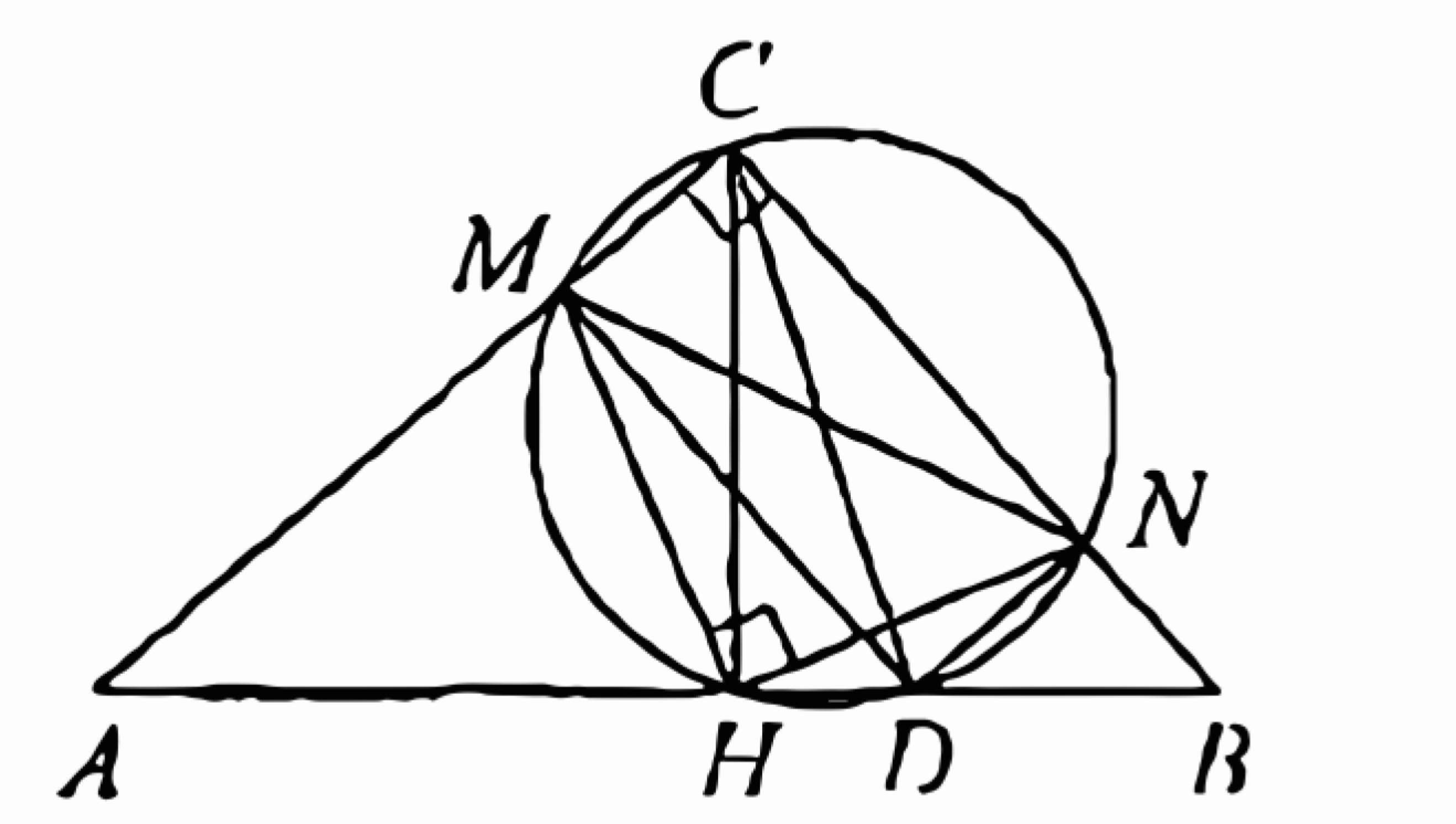
(ЕГЭ, 2021) Отрезок \(C H\) - высота прямоугольного треугольника \(A B C\) с прямым углом \(C\). На катетах \(A C\) и \(B C\) выбраны точки \(M\) и \(N\) соответственно такие, что \(\angle M H N=90^{\circ}\).
а) Докажите, что треугольник \(M N H\) подобен треугольнику \(A B C\).
б) Найдите \(C N\), если \(B C=2, A C=4, C M=1\).
Решение
a) В четырёхугольнике \(C M H N\) углы NCM и \(M H N\) равны \(90^{\circ}\). Следовательно, около этого четырёхугольника можно описать окружность. Значит,
\(\angle N M H=\angle N C H=90^{\circ}-\angle H B C=\angle B A C \text {. }\)
Таким образом, прямоугольные треугольники \(A B C\) и \(M N H\) подобны по острому углу.
б) Обозначим вторую точку пересечения окружности, описанной около четырёхугольника \(C M H N\), и отрезка \(A B\) через \(D\). Тогда \(C D\) - диаметр окружности, поскольку \(\angle C H D=90^{\circ}\). Значит \(\angle C N D=\angle C M D=\angle M C N=90^{\circ}\), следовательно, четырёхугольник \(C N D M\) - прямоугольник.
Таким образом,
\(C N=D M=A M \cdot \operatorname{tg} \angle B A C=\)
\((A C-C M) \cdot \dfrac{B C}{A C}=\dfrac{3}{2} .\)
Ответ
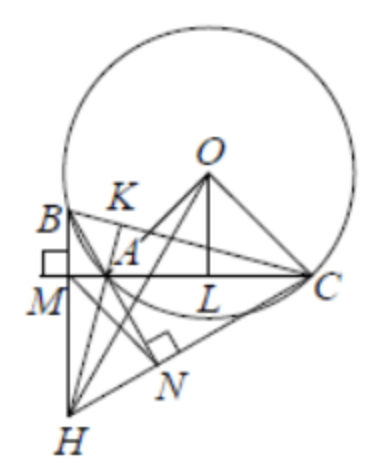
(ЕГЭ,2020) В треугольнике \(A B C\) угол \(A\) равен \(120^{\circ}\). Прямые, содержашие высоты \(B M\) и \(C N\) треугольника \(A B C\), пересекаются в точке \(H\). Точка \(O\) - центр окружности, описанной около треугольника \(A B C\).
a) Докажите, что \(A H=A O\).
б) Найдите плошадь треугольника \(A H O\), если \(B C=\sqrt{15}, \angle A B C=45^{\circ}\).
Решение
a) Точки \(M\) и \(N\) лежат на окружности диаметром \(B C\), поэтому \(\angle A M N=\angle C M N=\angle A B C\).
Значит, треугольники \(A M N\) и \(A B C\) подобны с коэффициентом подобия \(\frac{A N}{A C}=\cos \angle N A C=\cos 60^{\circ}=\frac{1}{2}\). Следовательно, радиус окружности, описанной около треугольника \(A M N\), равен \(\frac{A O}{2}\).
Точки \(M\) и \(N\) лежат на окружности диаметром \(A H\), поэтому \(A H=A O\).
б) Пусть прямые \(A H\) и \(B C\) пересекаются в точке \(K\), а точка \(L\) - середина стороны \(A C\), тогда
\(\angle A K B=90^{\circ}, \angle A O L=\frac{1}{2} \angle A O C=\frac{1}{2} \cdot 2 \angle A B C=\angle A B C=45^{\circ}\).
Значит
\(\angle O A L=90^{\circ}-\angle A O L=45^{\circ}, \angle B A K=90^{\circ}-\angle A B C=45^{\circ}\);
\(\angle O A H=180^{\circ}-\angle O A K=180^{\circ}-(\angle B A C-\angle B A K-\angle O A L)=150^{\circ}\)
Плошадь треугольника \(A H O\) равна
\(\frac{A O \cdot A H \cdot \sin \angle O A H}{2}=\frac{A O^2 \cdot \sin 150^{\circ}}{2}=\frac{B C^2 \cdot \sin 150^{\circ}}{8 \sin ^2 120^{\circ}}=\frac{5}{4}\)
Ответ
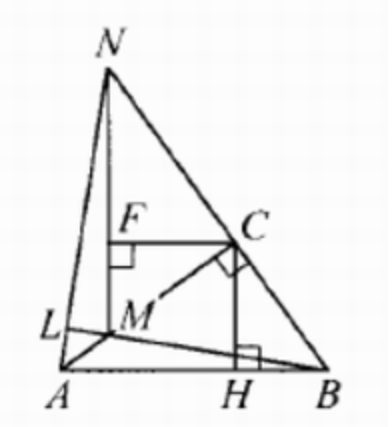
(ЕГЭ,2020) В прямоугольном треугольнике \(A B C\) точка \(M\) лежит на катете \(A C\), а точка \(N\) лежит на продолжении катета \(B C\) за точку \(C\), причём \(C M=B C\) и \(C N=A C\).
a) Отрезки \(C H\) и \(C F\) - высоты треугольников \(A C B\) и \(N C M\) соответственно. Докажите, что прямые \(C H\) и \(C F\) перпендикулярны.
б) Прямые \(B M\) и \(A N\) пересекаются в точке \(L\). Найдите \(L M\), если \(B C=4\), a \(A C=6\).
Решение
a) Прямоутольные треугольники \(A B C\) и \(N M C\) равны по двум катетам.
Пусть \(\angle B A C=\alpha\), тогда по свойству высоты в прямоугольном треугольнике:
\begin{equation*}
\angle A C H=90^{\circ}-\alpha, \angle F C M=\angle C N M=\angle C A B=\alpha \text {, }
\end{equation*}
откуда
\begin{equation*}
\angle F C H=\angle F C M+\angle A C H=\alpha+\left(90^{\circ}-\alpha\right)=90^{\circ} \text {. }
\end{equation*}
б) По условию \(C N=A C\) и \(C M=B C\), поэтому
\begin{equation*}
\angle L A M=\angle N A C=45^{\circ}, \angle A M L=\angle C M B=45^{\circ},
\end{equation*} откуда \(\angle A L M=90^{\circ}\), то есть \(A L M\) - равнобедренный прямоугольный треугольник. Значит,
\begin{equation*}
L M=\frac{\sqrt{2}}{2} A M=\frac{\sqrt{2}}{2}(A C-C M)=\frac{\sqrt{2}}{2}(A C-B C)=\sqrt{2} .
\end{equation*}
Ответ
(ЕГЭ,2020) На сторонах \(A B, B C\) и \(A C\) треугольника \(A B C\) отмечены точки \(C_1, A_1\) и \(B_1\) соответственно, причём \(A C_1: C_1 B=21: 10, B A_1: A_1 C=2: 3, A B_1: B_1 C=2: 5\). Отрезки \(B B_1\) и \(C C_1\) пересекаются в точке \(D\).
a) Докажите, что четырёхугольник \(A D A_1 B_1\) - параллелограмм.
б) Найдите \(C D\), если отрезки \(A D\) и \(B C\) перпендикулярны, \(A C=63\), \(B C=25\).
Решение
a) Проведём через точку \(B\) прямую, параллельную прямой \(A C\). Пусть эта прямая пересекает прямую \(C C_1\) в точке \(T\).
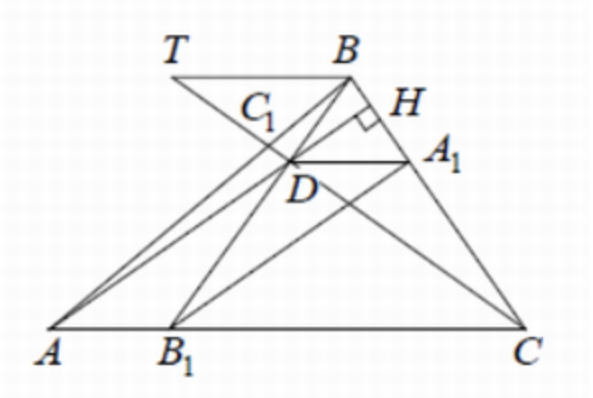
Тогда треугольники \(A C C_1\) и \(B T C_1\) подобны по двум углам, значит,
\begin{equation*}
\frac{B T}{A C}=\frac{B C_1}{A C_1}=\frac{10}{21} .
\end{equation*}
Треугольники \(B_1 C D\) и \(B T D\) также подобны по двум углам, следовательно,
\begin{equation*}
\frac{B D}{D B_1}=B T: C B_1=\frac{10 A C}{21}: \frac{5 A C}{7}=\frac{2}{3}=\frac{B A_1}{A_1 C} .
\end{equation*}
Таким образом, прямая \(A_1 D\) параллельна прямой \(A C\). Значит, треугольники \(D B A_1\) и \(B_1 B C\) подобны, следовательно,
\begin{equation*}
D A_1=\frac{B A_1}{B C} \cdot B_1 C=\frac{2}{5} \cdot \frac{5 A B_1}{2}=A B_1 .
\end{equation*}
Значит, в четырёхугольнике \(A D A_1 B_1\) противоположные стороны равны и параллельны, следовательно, он является параллелограммом.
б) Пусть прямые \(A D\) и \(B C\) пересекаются в точке \(H\), тогда
\begin{equation*}
A_1 H=\frac{A B_1}{B_1 C} \cdot A_1 C=\frac{2}{5} \cdot \frac{3 B C}{5}=6 .
\end{equation*}
В прямоугольном треугольнике \(D H A_1\) :
\begin{equation*}
A_1 D=A B_1=\frac{2 A C}{7}=18 ; D H^2=A_1 D^2-A_1 H^2=288 \text {. }
\end{equation*}
В прямоугольном треугольнике \(C D H\) :
\begin{equation*}
H C=A_1 H+A_1 C=21 ; C D=\sqrt{D H^2+H C^2}=27 .
\end{equation*}
Ответ
(ЕГЭ,2020) В остроугольном треугольнике \(A B C\) проведены высота \(C C_1\) и медиана \(A A_1\), причём точки \(A, C, A_1\) и \(C_1\) лежат на одной окружности.
a) Докажите, что треугольник \(A B C\) равнобедренный.
б) Найдите площадь треугольника \(A B C\), если \(A A_1: C C_1=3: 2\) и \(A_1 C_1=2\).
Решение
a) Вписанные углы \(A C_1 C\) и \(A A_1 C\) опираются на одну дугу \(A C\), значит, они равны, то есть \(\angle A A_1 C=90^{\circ}\).
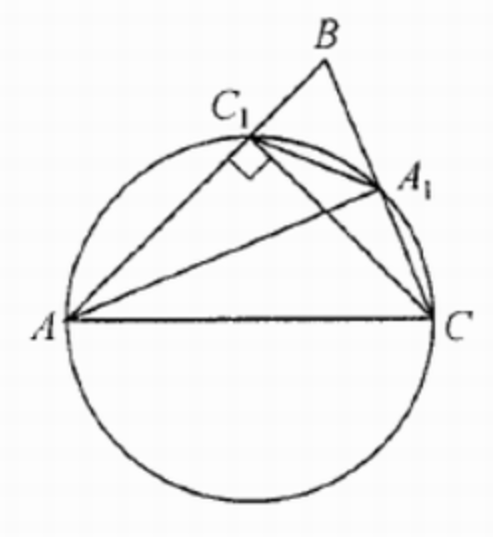
В треугольнике \(A B C\) медиана \(A A_1\) является высотой, значит, треугольник \(A B C\) равнобедренный, \(A B=A C\)
б) В прямоугольном треугольнике \(B C C_1\) медиана \(C_1 A_1\) равна половине гипотенузы, значит, \(B C=4\).
Прямоугольные треугольники \(A B A_1\) и \(C B C_1\) подобны по общему острому углу \(B\), значит, \(\frac{A B}{B C}=\frac{A A_1}{C C_1}=\frac{3}{2} ; A C=A B=\frac{3 B C}{2}=6\).
В прямоугольном треугольнике \(A C A_1\) получаем:
\begin{equation*}
A A_1=\sqrt{A C^2-C . A_1^2}=\sqrt{36-4}=4 \sqrt{2} \text {. }
\end{equation*}
Площадь треугольника \(A B C\) равна
\begin{equation*}
\frac{A A_1 B C}{2}=\frac{4 \sqrt{2} 4}{2}=8 \sqrt{2} \text {. }
\end{equation*}
Ответ
(ЕГЭ,2020) Биссектрисы острых углов \(A\) и \(B\) прямоугольного треугольника \(A B C\) пересекают окружность, описанную около этого треугольника, в точках \(A_1\) и \(B_1\) соответственно
a) Докажите, что угол \(A_1 B B_1\) равен \(45^{\circ}\)
б) Биссектриса угла с пересекает окружность, описанную около треугольника \(A B C\), точке \(C_1\). Найдите \(B_1 C_1\), если \(A B=2 \sqrt{3}, \angle B A C=60^{\circ}\)
Решение
a) Биссектрисы вписанных углов делят дуги, на которые опираются эти углы, пополам.
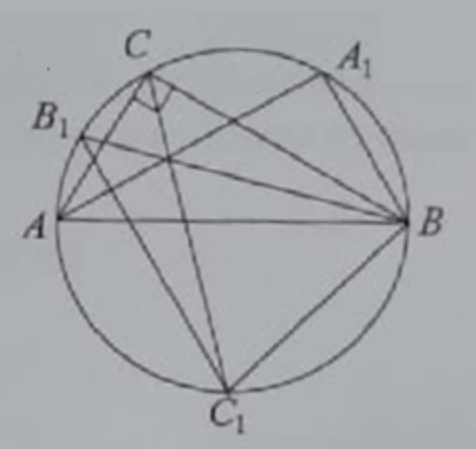
Значит, дуга \(C B_1\) равна половине дуги \(A C\), а дуга \(C A_1\) равна половине дуги \(B C\). Вписанный угол \(A_1 B B_1\) равен половине дуги \(A_1 B_1\), которая равна половине дуги \(A B\), составляющей половину окружности. Следовательно,
\begin{equation*}
\angle A_1 B B_1=\frac{1}{2} \cdot \frac{1}{2} \cdot 180^{\circ}=45^{\circ} .
\end{equation*}
б) Поскольку \(\angle A C C_1=\angle B C C_1\), точка \(C_1\) - середина дуги \(A B\), составляющей половину окружности, то есть \(\angle A B C_1=45^{\circ}\). Поскольку луч \(B B_1\) - биссектриса угла \(A B C\),
\begin{equation*}
\angle A B B_1=\frac{1}{2} \angle A B C=\frac{90^{\circ}-60^{\circ}}{2}=15^{\circ} ; \angle B_1 B C_1=\angle A B B_1+\angle A B C_1=60^{\circ} .
\end{equation*}
Отрезок \(A B\) - диаметр окружности, описанной около прямоугольного треуготьника \(A B C\). По теореме синусов в треугольнике \(B B_1 C_1\) имеем: \(B_1 C_1=A B \cdot \sin \angle B_1 B C_1=3\).
