17. Планиметрия
Чтобы получить дополнительный функционал нужно войти.
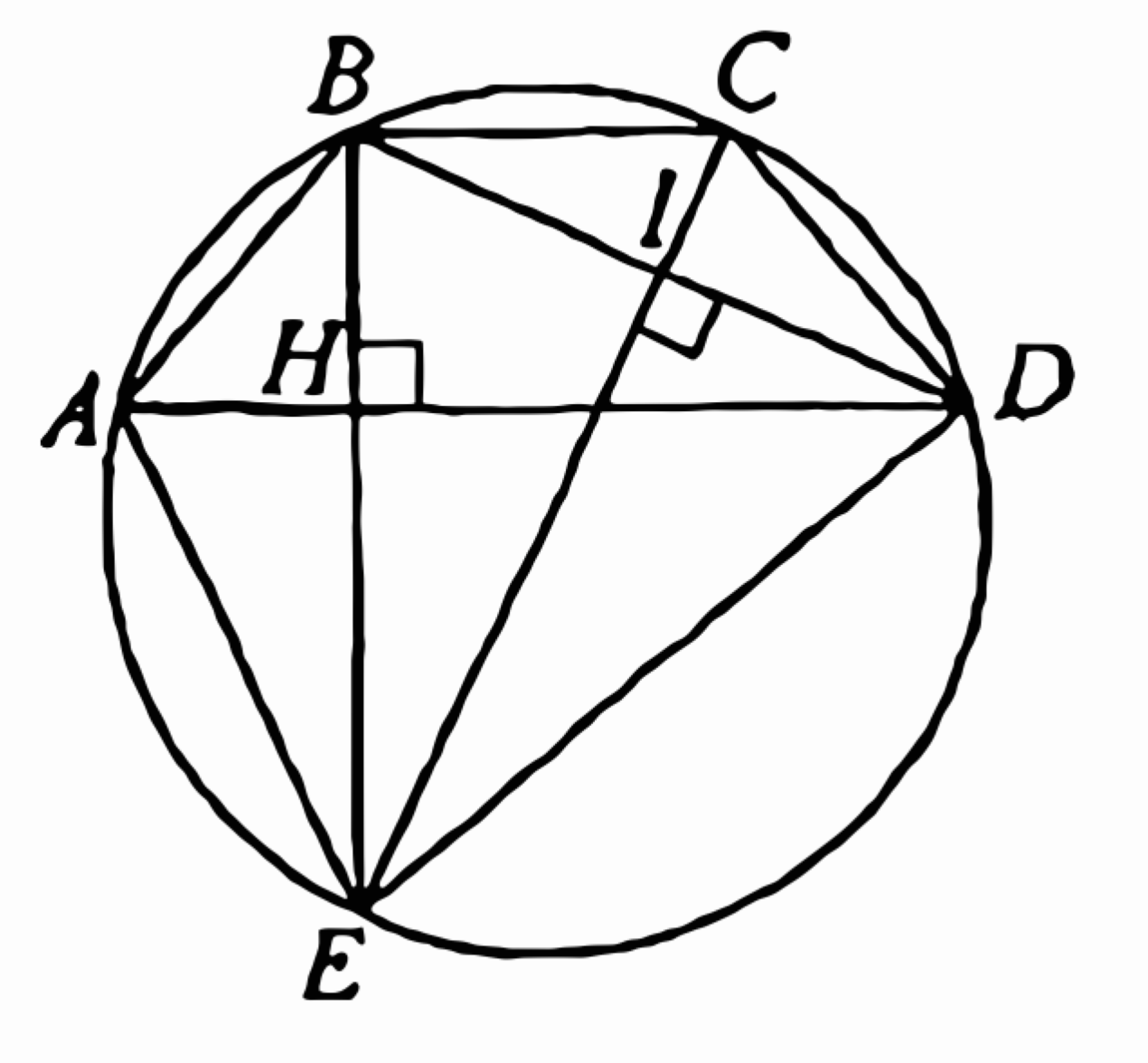
(ЕГЭ, 2022) Точка \(D\) лежит на основании \(A C\) равнобедренного треугольника \(A B C\)
Точки \(I\) и \(J\) - центры окружностей, описанных около треугольников \(A B D\) и \(C B D\) соответственно.
a) Докажите, что прямые \(B I\) и \(D J\) параллельны.
б) Найдите \(I J\), если \(A C=12, \cos \angle B D C=\dfrac{3}{7}\).
Решение
a) Радиусы окружностей, описанных около треугольников \(A B D\) и \(C B D\), равны \(\dfrac{A B}{2 \sin \angle A D B}\) и \(\dfrac{B C}{2 \sin \angle B D C}\) соответственно.
Поскольку \(\quad \angle A D B=180^{\circ}-\angle B D C\) и \(A B=B C\), радиусы окружностей, описанных около треугольников \(A B D\) и \(C B D\), равны.
Следовательно, четырёхугольник \(B I D J\) является ромбом. Значит, прямые \(B I\) и \(D J\) параллельны.
б) Обозначим середины отрезков \(A D\) и \(D C\) через \(N\) и \(K\) соответственно.
Поскольку центр описанной около треугольника окружности лежит на серединном перпендикуляре к каждой из его сторон, прямые \(I N\) и \(J K\) перпендикулярны прямой \(A C\), а прямая \(I J\) перпендикулярна прямой \(B D\).
Стороны углов \(N I J\) и \(C D B\) соответственно перпендикулярны, значит, эти углы равны.
Отрезок \(N K\) является проекцией отрезка \(I J\) на прямую \(A C\). Следовательно, \(N K=I J \sin \angle N I J \).
\( I J=\dfrac{N K}{\sin \angle C D B}=\dfrac{N D+D K}{\sqrt{1-\cos ^2 \angle C D B}}=\)
\(\dfrac{0,5 A D+0,5 C D}{\dfrac{2 \sqrt{10}}{7}}=\dfrac{7 A C}{4 \sqrt{10}}=\dfrac{21 \sqrt{10}}{10} .\)
Ответ
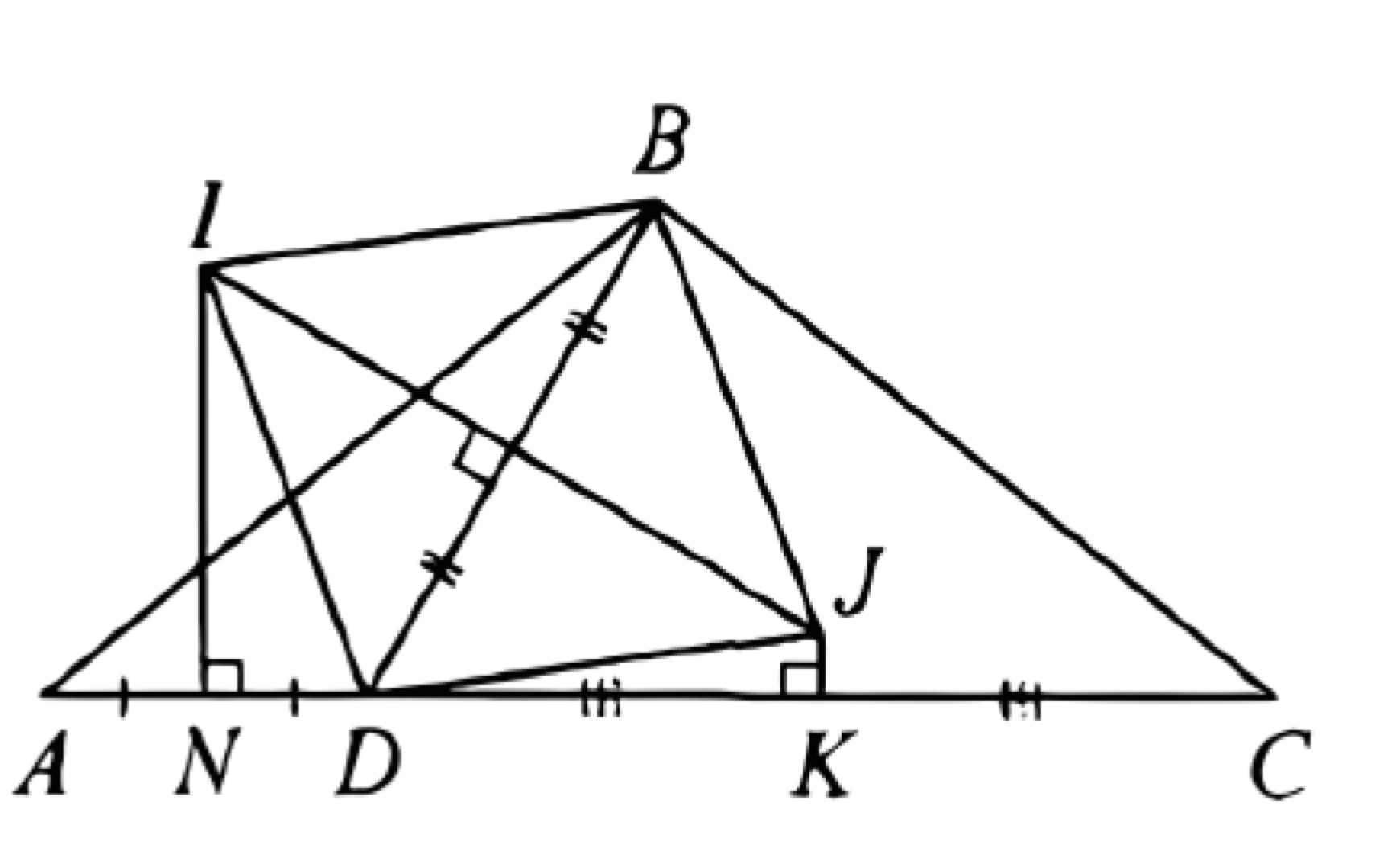
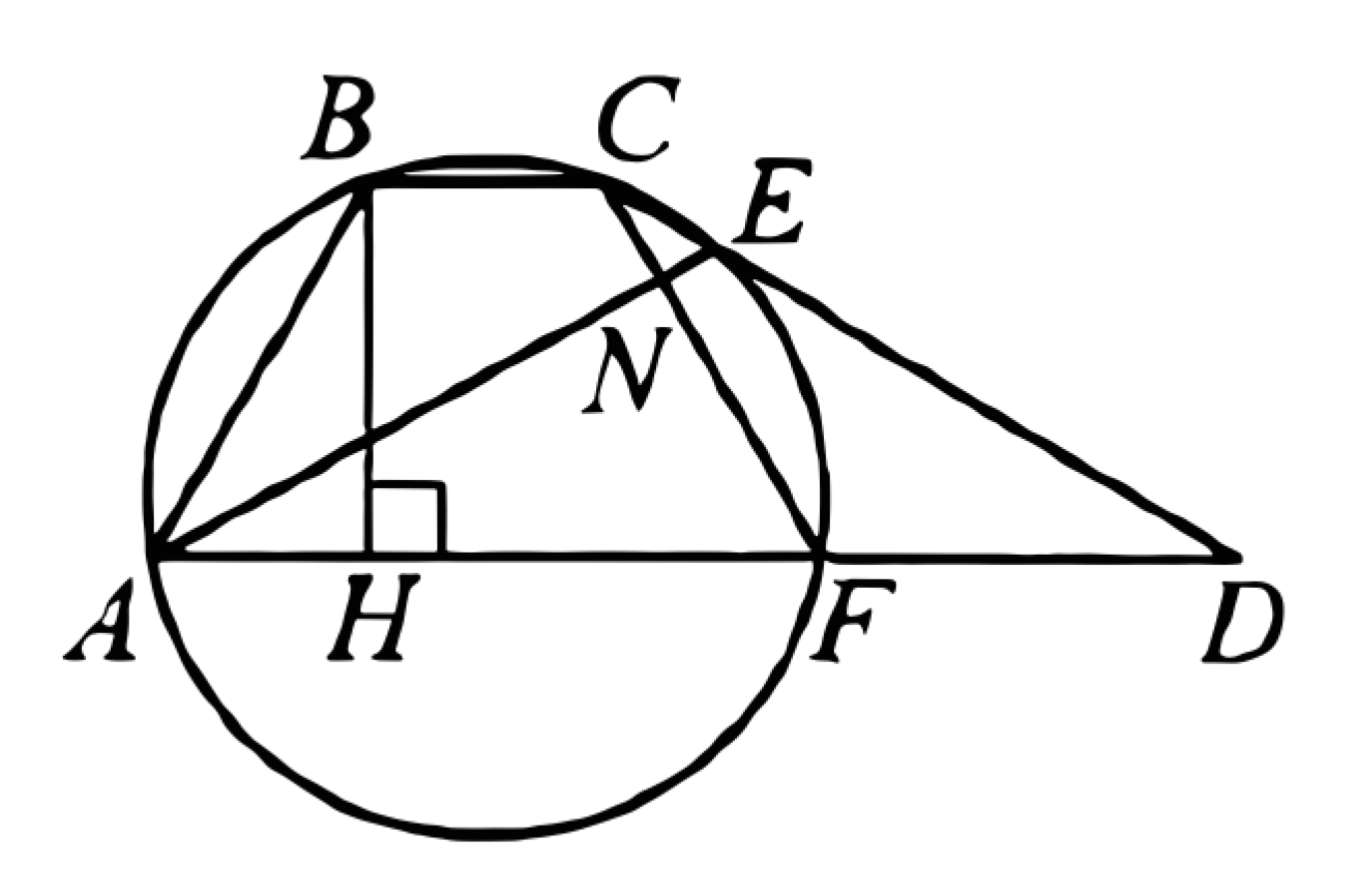
(ЕГЭ, 2021) Дана трапеция \(A B C D\) с основаниями \(A D\) и \(B C\). Окружность, описанная около треугольника \(A B C\), пересекает боковую сторону \(C D\) в точке \(E\), а основание \(A D\) в точке \(F\), причём \(A B=F D\).
a) Докажите, что \(\angle E A D=\angle E D A\).
б) Найдите площадь трапеции \(A B C D\), если \(A B=5, B C=3\), а прямые \(A E\) и \(C F\) перпендикулярны.
Решение
a) Трапеция \(A B C F\) вписана в окружность, поэтому \(C F=A B=F D\). Значит, треугольник \(C F D\) равнобедренный и
\(\angle E D A=\angle C D F=\angle F C D=\angle F C E=\)
\(\angle F A E=\angle E A D \text {. }\)
б) Пусть \(B H\) - высота трапеции \(A B C F\), а \(N\) точка пересечения прямых \(A E\) и \(C F\).
В треугольнике \(A N F\) имеем:
\(\angle N A F=90^{\circ}-\angle N F A=\)
\(90^{\circ}-\angle F C D-\angle F D C=90^{\circ}-2 \angle N A F \text {. }\)
Значит, \(\angle N A F=30^{\circ} ; \angle B A F=\angle C F A=\angle N F A=60^{\circ}\)
Следовательно,
\(B H=A B \cdot \sin 60^{\circ}=\dfrac{5 \sqrt{3}}{2},\)
\(A H=A B \cdot \cos 60^{\circ}=\dfrac{5}{2} ; A F=2 A H+B C=8 ; \)
\(S_{A B C D}=B H \cdot \dfrac{B C+A D}{2}=\)
\(B H \cdot \dfrac{B C+A F+F D}{2}=20 \sqrt{3} .\)
Ответ
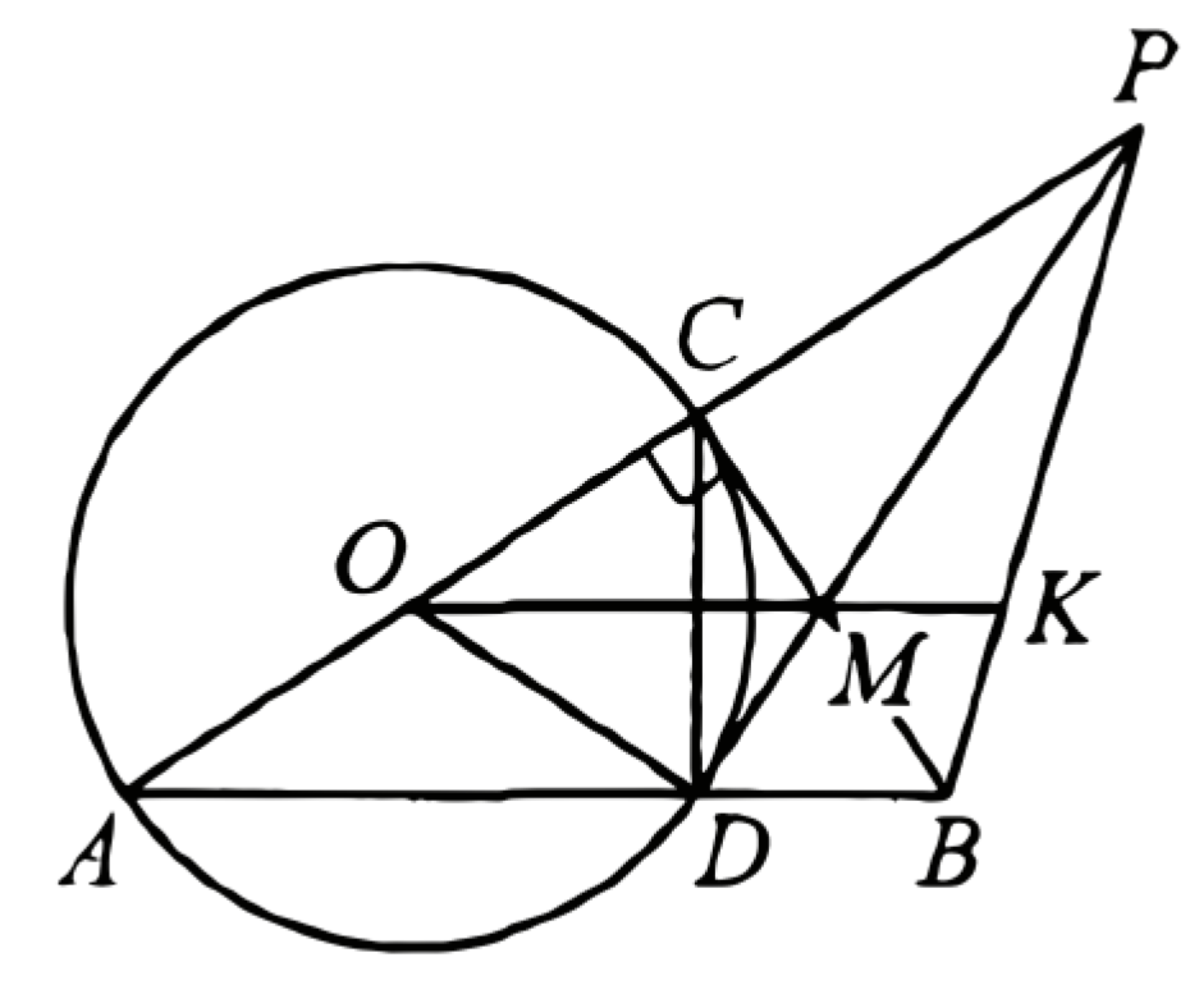
(ЕГЭ, 2021) Окружность с центром \(O\), построенная на катете \(A C\) прямоугольного треугольника \(A B C\) как на диаметре, пересекает гипотенузу \(A B\) в точках \(A\) и \(D\). Касательная, проведённая к этой окружности в точке \(D\), пересекает катет \(B C\) в точке \(M\).
a) Докажите, что \(B M=C M\).
б) Прямая \(D M\) пересекает прямую \(A C\) в точке \(P\), прямая \(O M\) пересекает прямую \(B P\) в точке \(K\). Найдите \(B K: K P\), если \(\cos \angle B A C=\dfrac{2 \sqrt{5}}{5}\).
Решение
a) Отрезок \(C D\) является высотой треугольника \(A B C\), поскольку вписанный угол \(A D C\) опирается на диаметр окружности. Прямая \(B C\) касается окружности с диаметром \(A C\) в точке \(C\), поскольку радиус окружности \(O C\) перпендикулярен \(B C\).
Следовательно,\(\quad C M=M D \quad\) как \(\quad\) отрезки касательных, проведённых из одной точки. Значит,
\(\angle M B D=90^{\circ}-\angle M C D=\)
\(90^{\circ}-\angle M D C=\angle M D B,\)
поэтому \(B M=M D=C M\).
б) Прямые \(A B\) и \(O M\) параллельны, поскольку отрезок \(O M\) - средняя линия треугольника \(A B C\). Значит, \(B K: K P=A O: O P\).
Обозначим угол \(B A C\) через \(\alpha\). Тогда
\(\angle C O D=2 \alpha, \angle O D P=90^{\circ} ;\)
\(O P=\dfrac{O D}{\cos 2 \alpha} .\)
Значит,
\(B K: K P=A O: O P=O D: \dfrac{O D}{\cos 2 \alpha}=\)
\(\cos 2 \alpha=2 \cos ^2 \alpha-1=\dfrac{3}{5} .\)
Ответ
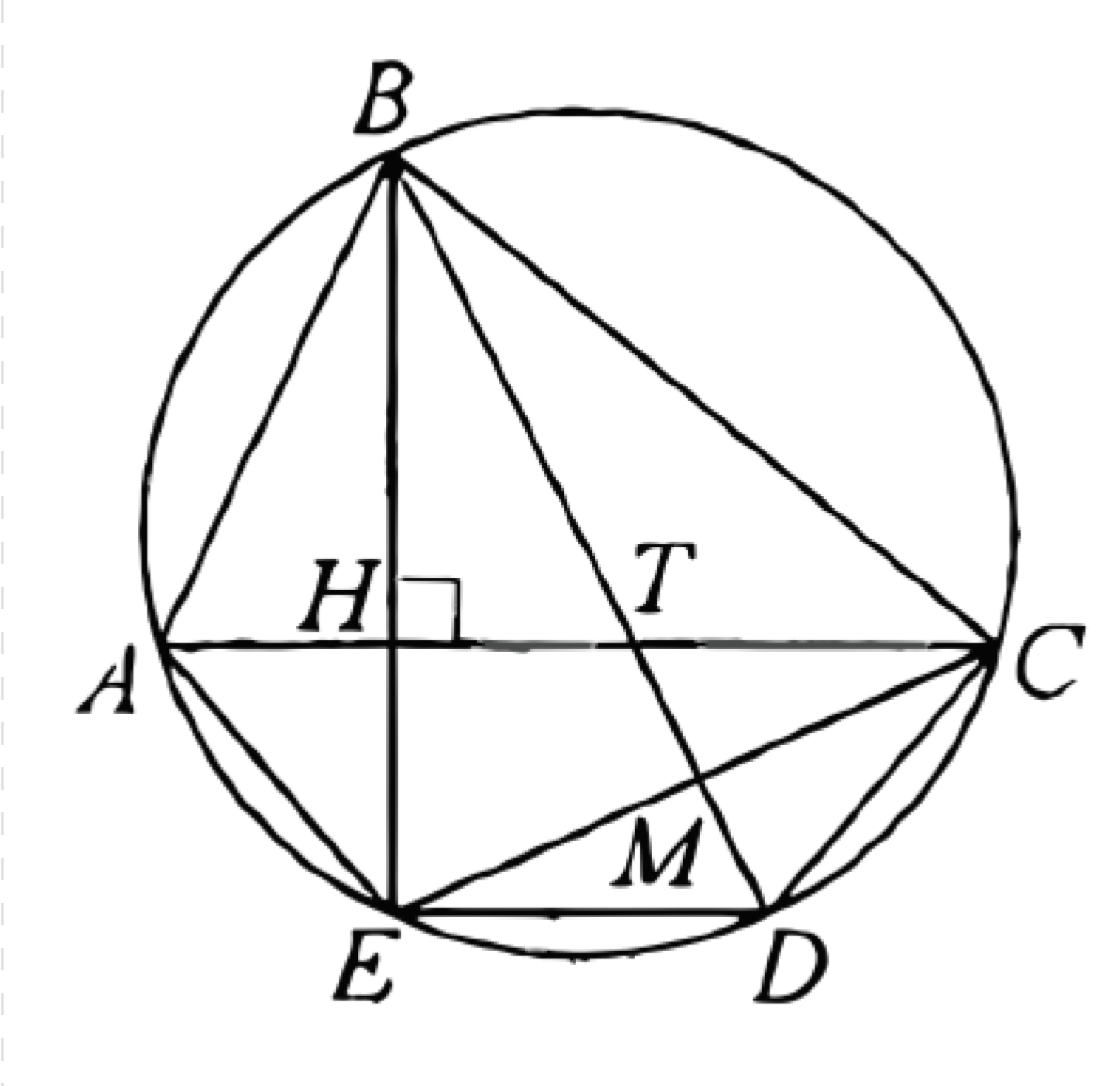
(ЕГЭ, 2021) Точки \(A, B, C, D\) и \(E\) лежат на окружности в указанном порядке, причём \(A E=E D=C D\), а прямые \(A C\) и \(B E\) перпендикулярны. Отрезки \(A C\) и \(B D\) пересекаются в точке \(T\).
a) Докажите, что прямая \(E C\) пересекает отрезок \(T D\) в его середине.
б) Найдите площадь треугольника \(A B T\), если \(B D=6, A E=\sqrt{6}\).
Решение
a) Обозначим точку пересечения прямой \(E C\) и отрезка \(T D\) через \(M\), а точку пересечения отрезков \(A C\) и \(B E\) через \(H\). Угол \(B M C\) равен полусумме дуг \(B C\) и \(D E,\) а угол \(B H C\) равен полусумме дуг \(B C\) и \(A E\).
Дуги \(A E, E D\) и \(C D\) меньше \(180^{\circ}\) и стягиваются равными хордами. Следовательно, эти дуги равны. Значит,
\(\angle B M C=\angle B H C=90^{\circ} \text { и } \angle A C E=\angle D C E\).
В треугольнике \(\quad T C D\) отрезок \(\quad C M\) является биссектрисой и высотой, поэтому этот треугольник равнобедренный, \(T C=C D\), а точка \(M\) - середина отрезка \(T D\).
б) Дуги \(A E\) и \(C D\) равны, значит, \(\angle A C E=\angle C E D\), следовательно, прямые \(A C\) и \(D E\) параллельны, а \(\angle B E D=90^{\circ}\).
Обозначим \(\angle D B E\) через \(\alpha\). Тогда
\(\sin \alpha=\dfrac{E D}{B D}=\dfrac{A E}{B D}=\dfrac{\sqrt{6}}{6} : \cos \alpha=\dfrac{\sqrt{30}}{6}\).
\(\angle A B E=\angle D B E=\angle D B C=\alpha ;\)
\(\angle E A C=\angle E B C=2 \alpha .\)
В треугольнике \(A B T\) отрезок \(B H\) является биссектрисой и высотой, поэтому этот треугольник равнобедренный, \(A B=B T\), а точка \(H\) - середина отрезка \(A T\).
Получаем:
\(A H=A E \cdot \cos \angle E A C=A E \cdot \cos 2 \alpha=\)
\(A E \cdot\left(1-2 \sin ^2 \alpha\right)=\dfrac{2 \sqrt{6}}{3} ; \)
\(A T=2 A H=\dfrac{4 \sqrt{6}}{3} ; B H=A H \cdot \operatorname{ctg} \angle A B H=\)
\(A H \cdot \operatorname{ctg} \alpha=\dfrac{2 \sqrt{30}}{3} .\)
Значит, площадь треугольника \(A B T\) равна
\(\dfrac{A T \cdot B H}{2}=\dfrac{8 \sqrt{5}}{3} .\)
Ответ
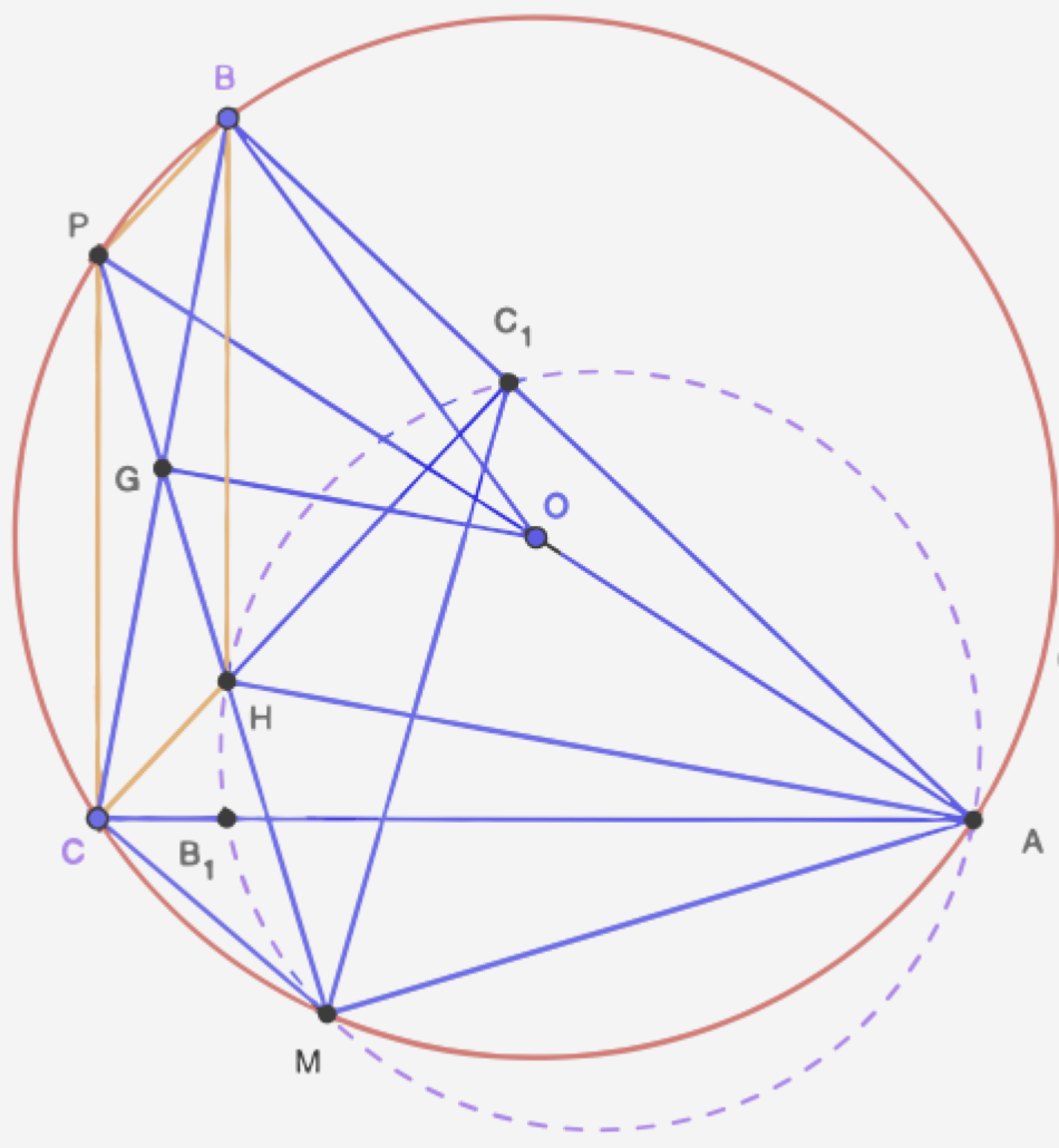
(ЕГЭ, 2021) Высоты \(B B_1\) и \(C C_1\) остроугольного треугольника \(A B C\) пересекаются в точке \(H\).
Отрезок \(A P\) - диаметр окружности, описанной около треугольника \(A B C\).
а) Докажите, что прямая \(H P\) пересекает отрезок \(B C\) в его середине.
б) Луч \(P H\) вторично пересекает окружность, описанную около треугольника \(A B C\), в точке \(M\). Найдите длину отрезка \(M C_1\), если расстояние от центра этой окружности до прямой \(B C\) равно \(4, \angle B P H=120^{\circ}\).
Решение
a) Пусть ( \(\mathrm{BC}) \cap(\mathrm{PH})=\mathrm{G}\);
\(\angle \mathrm{PCA}=90^{\circ}\) (опирается на диаметр) \(\Rightarrow \mathrm{PC} \perp \mathrm{AC}\), но \(\mathrm{BH} \perp \mathrm{AC} \Rightarrow \mathrm{PC} \| \mathrm{BH}\);
аналогично \(\mathrm{CH} \| \mathrm{BP} \Rightarrow\)
\(\mathrm{CPBH}\) - параллелограмм, диагонали которого пересекаются в их середине \(\Rightarrow \mathrm{G}-\) середина \(\mathrm{BC}\)
б) \(\mathrm{OG} \perp \mathrm{BC}\) (по свойству диаметра, проходящего через середину хорды ) \(\Rightarrow \mathrm{OG}=4\);
\(\mathrm{OG}-\) средняя линия \(\triangle \mathrm{HPA} \Rightarrow \mathrm{AH}=2 . \mathrm{OG}=8\); из точек \(\mathrm{M}\) и \(\mathrm{C}_1\) отрезок \(\mathrm{AH}\) виден под прямым углом \(\Rightarrow\)
точки \(\mathrm{M}, \mathrm{H}, \mathrm{C}_1, \mathrm{A}\) лежат на одной окружности с диаметром \(\mathrm{AH}\)
\(R=\dfrac{A H}{2}=4 ;\)
Так как MPBA - вписанный , то \(\angle \mathrm{MAB}=180^{\circ}-\angle \mathrm{P}=60^{\circ} \)
\(\text { из } \triangle \mathrm{MAC}_1: M \mathrm{C}_1=2 R \cdot \sin A=8 \cdot \dfrac{\sqrt{3}}{2}=4 \sqrt{3}\)
Ответ
(ЕГЭ, 2021) В равнобедренной трапеции \(A B C D\) меньшее основание \(B C\) равно боковой стороне. На плоскости выбрали точку \(E\) такую, что прямая \(B E\) перпендикулярна прямой \(A D\), а прямая \(C E\) перпендикулярна прямой \(B D\).
a) Докажите, что \(\angle A E B=\angle A D B\).
б) Найдите площадь трапеции \(A B C D\), если \(A B=32, \cos \angle A E B=\dfrac{3}{4}\).
Решение
a) Обозначим точку пересечения прямых \(A D\) и \(B E\) через \(H\), а точку пересечения прямых \(B D\) и \(C E\) через \(I\).
\(\mathrm{B}\) равнобедренной трапеции \(A B C D\) сумма противоположных углов равна \(180^{\circ}\), следовательно, около неё можно описать окружность.
В равнобедренном треугольнике \(B C D\): \(\angle C B D=\angle C D B \text {. }\)
В прямоугольном треугольнике \(B C E\): \(\angle B E C=90^{\circ}-\angle I B E=\angle C B D=\angle C D B \text {. }\)
Следовательно, точка \(E\) лежит на окружности, описанной около треугольника \(B C D\), то есть точки \(A, B, C, D\) и \(E\) лежат на одной окружности. Значит, \(\angle A E B=\angle A D B\).
б) Обозначим \(\angle A E B\) через \(\alpha\). Тогда \(\sin \alpha=\dfrac{\sqrt{7}}{4}, \quad \operatorname{tg} \alpha=\dfrac{3 \sqrt{7}}{7}\), \(\angle A D B=\angle A E B=\alpha\).
Дуги \(A B, B C\) и \(C D\) меньше \(180^{\circ}\) и стягиваются равными хордами, следовательно, эти дуги равны, откуда \(\angle B A D=\angle C D A=2 \alpha\).
Получаем:
\(A H=A B \cdot \cos 2 \alpha=A B \cdot\left(2 \cos ^2 \alpha-1\right)=4 ; \)
\(B H=A B \cdot \sin 2 \alpha=A B \cdot 2 \sin \alpha \cdot \cos \alpha=12 \sqrt{7} ; \)
\(H D=B H \cdot \operatorname{ctg} \angle B D H=B H \cdot \operatorname{ctg} \alpha=36 \)
\(A D=A H+H D=40, B C=A B=32\)
Значит, площадь трапеции \(A B C D\) равна
\(B H \cdot \dfrac{B C+A D}{2}=432 \sqrt{7} \text {. }\)