17. Планиметрия
Чтобы получить дополнительный функционал нужно войти.
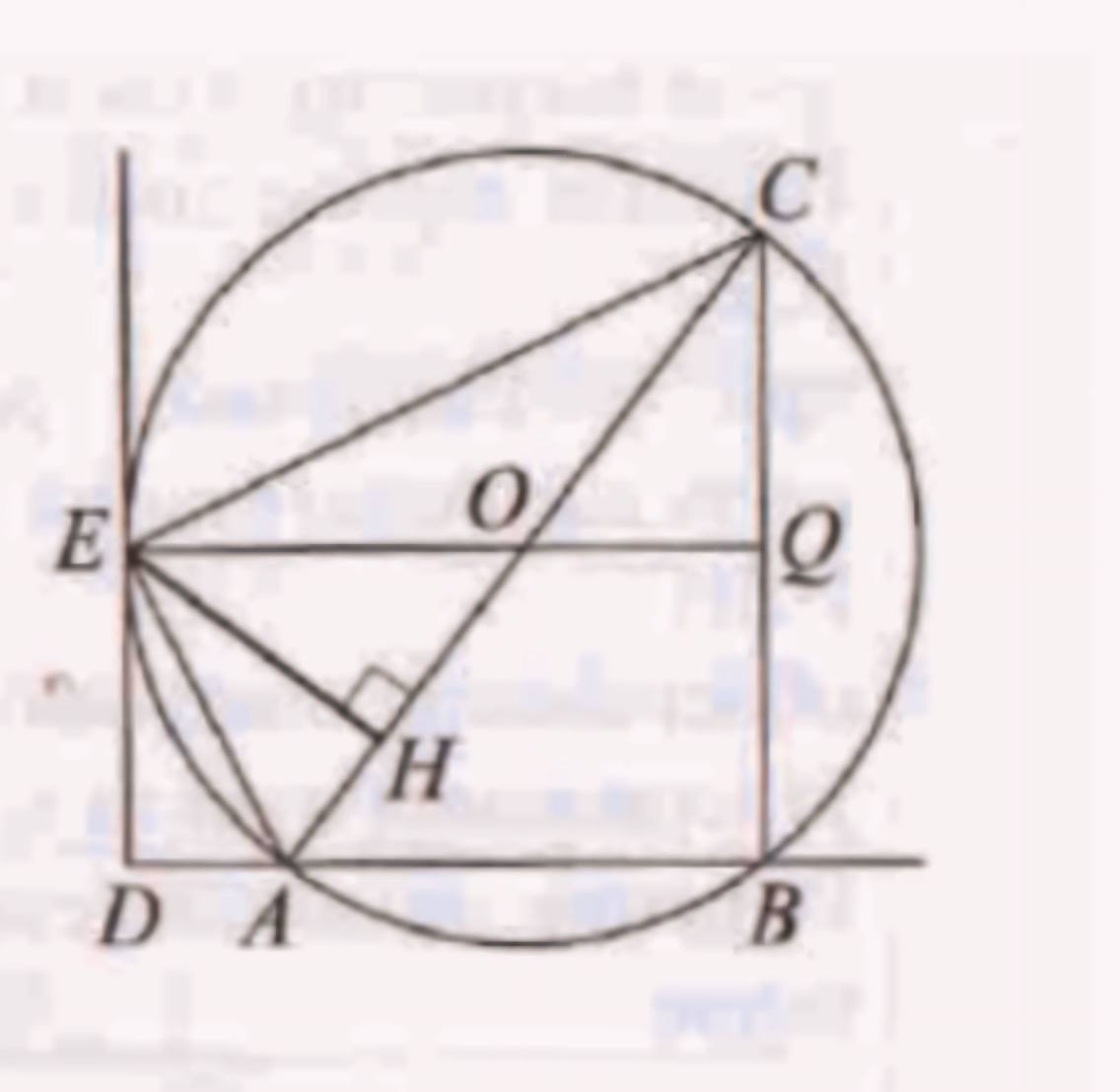
(ЕГЭ, 2023) Окружность касается одной из сторон прямого угла с вершиной \(D\) в точке \(E\) и пересекает вторую сторону в точках \(A\) и \(B\) (точка \(A\) лежит между \(B\) и \(D\) ). В окружности проведён диаметр \(A C\).
а) Докажите, что отрезок \(B C\) вдвое больше отрезка \(D E\).
б) Найдите расстояние от точки \(E\) до прямой \(A C\), если \(A D=4\) и \(A B=5\).
Решение
a) Пусть \(O\) - центр окружности, а прямая \(E O\) пересекает \(B C\) в точке \(Q\).
Радиус \(O E\) перпендикулярен касательной \(D E\), следовательно, прямые \(E O\) и \(A B\) параллельны. Вписанный угол \(A B C\) прямой. Значит, прямые \(C B\) и \(E D\) параллельны. Четырёхугольник BQED прямоугольник. Отрезок \(O Q\) - перпендикуляр к хорде \(B C\). Значит, \(Q\) - середина \(B C\). Тогда \(B C=2 B Q=2 D E\).
б) По теореме о касательной и секущей:
\(D E^2=A D \cdot(A D+A B)=4(4+5)=36 ;\)
\(D E=6\)
Тогда \(B C=2 D E=12\). По теореме Пифагора:
\(A E^2=A D^2+D E^2=16+36=52 ; \)
\(A E=2 \sqrt{13} .\)
Так как \(A C\) - диаметр окружности, углы \(A B C\) и \(A E C\) прямые. Поэтому:
\(A C^2=A B^2+B C^2=25+144=169 ; \)
\(A C=13 ; \)
\(C E=\sqrt{A C^2-A E^2}=\sqrt{169-52}=3 \sqrt{13} \)
Перпендикуляр \(E H\), опущенный из точки \(E\) на прямую \(A C\), - высота прямоугольного треугольника \(A E C\), проведённая из вершины прямого угла, следовательно,
\begin{equation*}
E H=\dfrac{C E \cdot A E}{A C}=\dfrac{3 \sqrt{13} \cdot 2 \sqrt{13}}{13}=6 .
\end{equation*}
Ответ
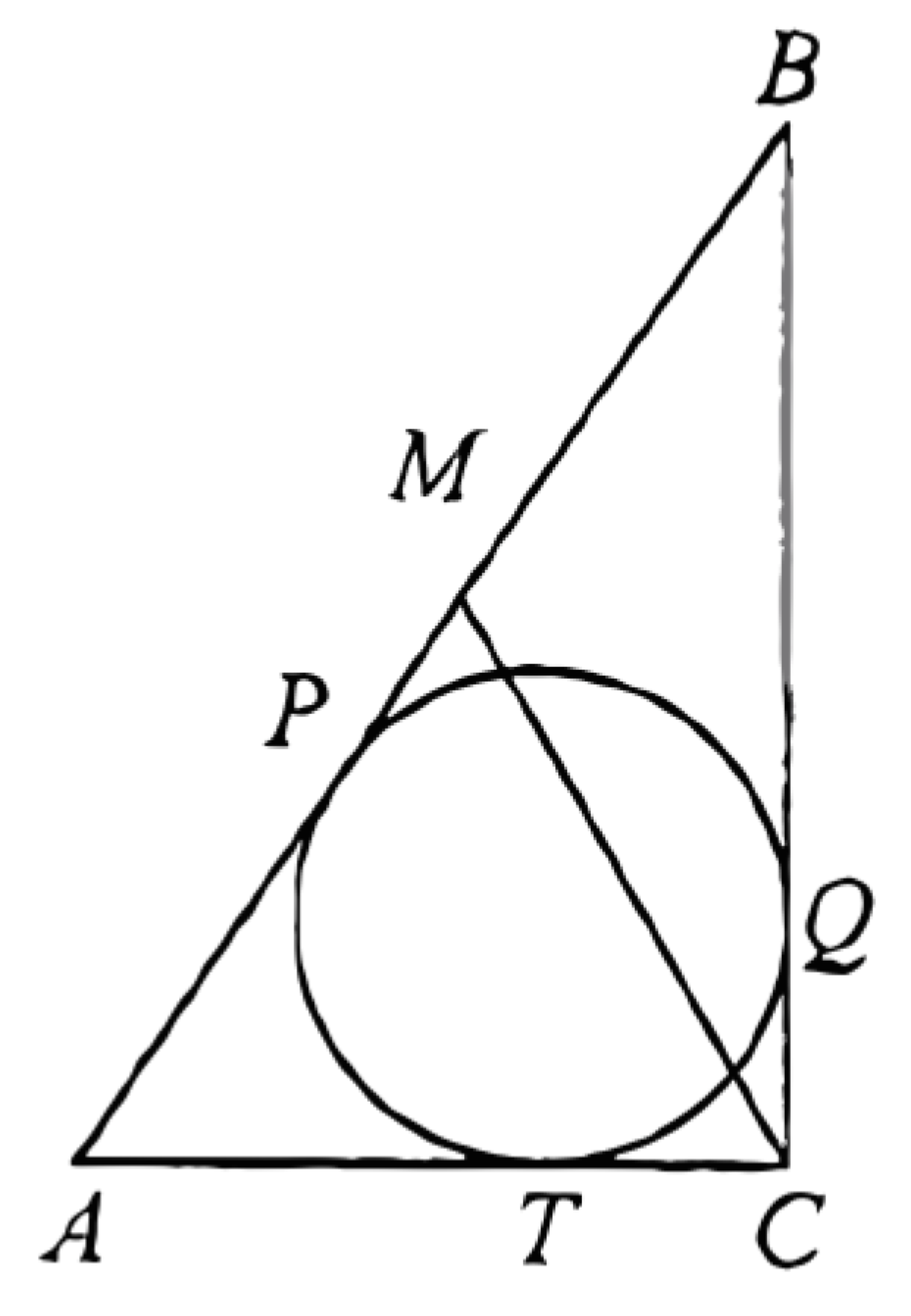
(ЕГЭ, 2022) Точка \(M\) - середина стороны \(A B\) треугольника \(A B C\). Окружность, вписанная в треугольник \(A B C\), касается стороны \(A B\) в точке \(P\).
а) Докажите, что \(M P=\dfrac{|B C-A C|}{2}\).
б) Известно, что \(M C=M A, B C>A C\), а отрезок \(M P\) относится к радиусу окружности, вписанной в треугольник \(A B C\), как \(7: 4\).
Найдите углы треугольника \(A B C\).
Решение
a) Обозначим точки касания окружности с отрезками \(B C\) и \(A C\) через \(Q\) и \(T\) соответственно.
По свойству касательных: \(A P=A T, C T=C Q, B P=B Q;\)
\(B C-A C=B Q+Q C-T C-A T=\)
\(B Q-A T= B P-A P=A B-2 A P=\)
\(2 A M-2 A P; M P=|A M-A P|=\)
\(\dfrac{|B C-A C|}{2}\).
б) Поскольку \(M C=M A=M B, \quad\) точка \(C\) лежит на окружности с диаметром \(A B\), а значит, \(\angle A C B=90^{\circ}\), следовательно, радиус вписанной окружности треугольника \(A B C\) равен \(C T=C Q\).
Пусть \(C T=r, A T=x\), тогда \(M P=\dfrac{7}{4} r, A C=x+r\). Поскольку \(B C>A C\) и \(\angle A C B=90^{\circ}\), получаем:
\(B C=2 M P+A C=\dfrac{9}{2} r+x, \)
\(A M=A P+M P=A T+M P=x+\dfrac{7}{4} r ;\)
\(A B=2 x+\dfrac{7}{2} r .\)
По теореме Пифагора в треугольнике \(A B C\) :
\(A B^2=A C^2+B C^2 ;\)
\(\left(2 x+\dfrac{7}{2} r\right)^2= (x+r)^2+\left(x+\dfrac{9}{2} r\right)^2 ;\)
\(2 x^2+3 x r-9 r^2=0 ; \)
\((x+3 r)(2 x-3 r)=0 .\)
Получаем:
\(x=\dfrac{3}{2} r ; A C=x+r=\dfrac{5}{2} r, \)
\(B C=x+\dfrac{9}{2} r=6 r, \operatorname{tg} \angle B A C=\)
\(\dfrac{B C}{A C}=\dfrac{12}{5}, \operatorname{tg} \angle A B C=\dfrac{5}{12} .\)
Углы треугольника \(A B C\) равны \(90^{\circ}, \operatorname{arctg} \dfrac{12}{5}, \operatorname{arctg} \dfrac{5}{12}\).
Ответ
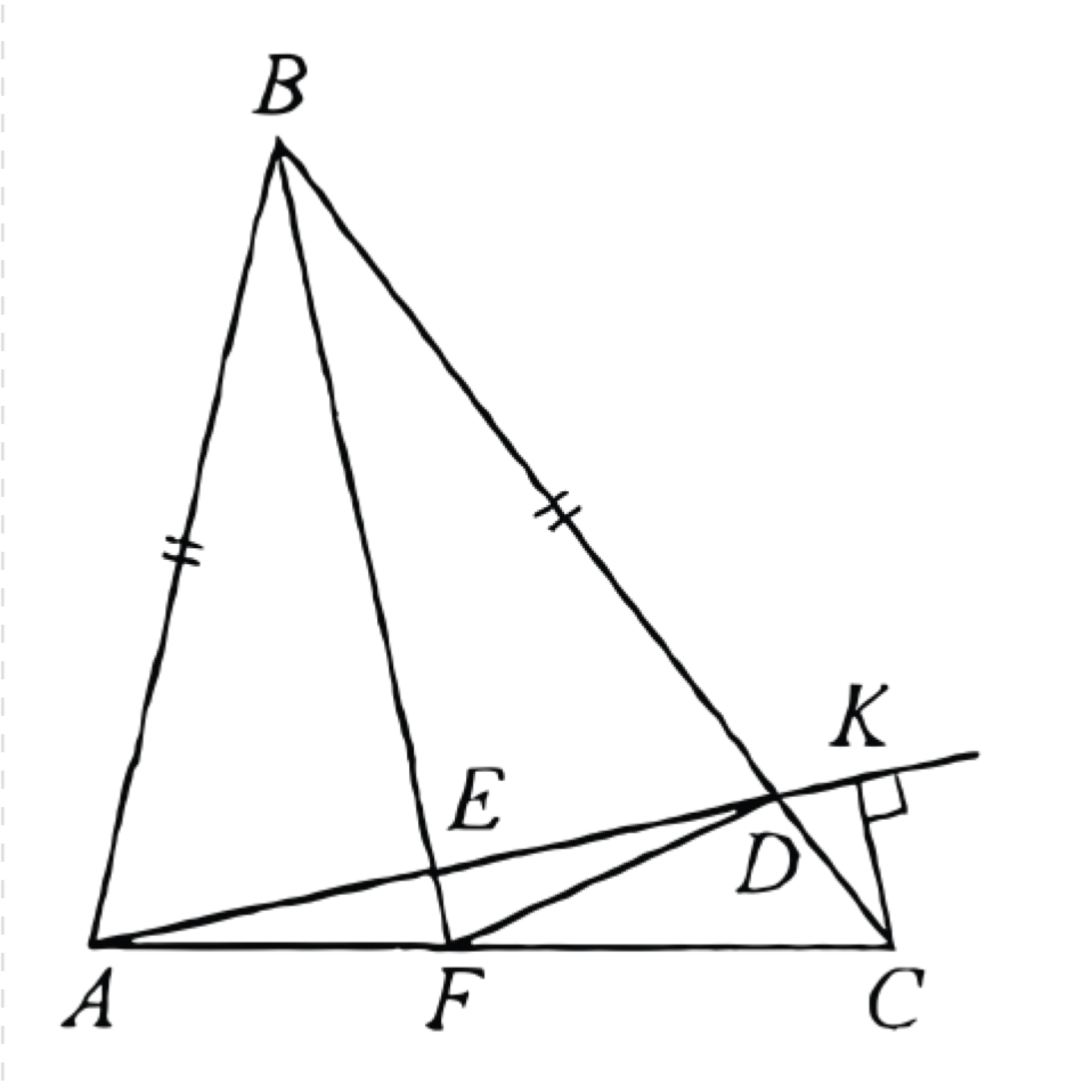
(ЕГЭ, 2022) На стороне \(B C\) треугольника \(A B C\) отмечена точка \(D\) так, что \(A B=B D\). Биссектриса \(B F\) треугольника \(A B C\) пересекает прямую \(A D\) в точке \(E\). Из точки \(C\) на прямую \(A D\) опущен перпендикуляр \(C K\).
a) Докажите, что \(A B: B C=A E: E K\).
б) Найдите отношение площади треугольника \(A B E\) к площади четырёхугольника \(C D E F\), если \(B D: D C=5: 2\).
Решение
a) В равнобедренном треугольнике \(A B D\) биссектриса \(B E\) является медианой и высотой. Следовательно, прямые \(B F\) и \(C K\) перпендикулярны прямой \(A K\), а значит, параллельны.
По свойству биссектрисы треугольника \(A B: B C=A F: F C\), а по теореме Фалеса \(A F: F C=A E: E K\). Таким образом, \(A B: B C=A E: E K\).
б) Прямоугольные треугольники \(B E D\) и \(C K D\) подобны по острому углу \((\angle B D E=\angle C D K)\), откуда получаем: \(B E: C K=B D: C D=5: 2 \text {. }\)
Прямоугольные треугольники \(A E F\) и \(A K C\) подобны по общему острому углу\(A\),
откуда:
\(\dfrac{E F}{K C}=\dfrac{A E}{A K}=\dfrac{A E}{A E+E K}=\)
\(\dfrac{1}{1+\dfrac{E K}{A E}}=\dfrac{1}{1+\dfrac{B C}{A B}}=\)
\(\dfrac{1}{1+\dfrac{B C}{B D}}=\dfrac{1}{1+\dfrac{7}{5}}=\dfrac{5}{12} ; \)
\(B E: E F=\dfrac{B E}{C K} \cdot \dfrac{C K}{E F}=\dfrac{5}{2} \cdot \dfrac{12}{5}=6 .\)
Обозначим площади многоугольников \(A B E, B D E, D E F, B F D, C F D\) и \(C D E F\)
через \(S, S_{B D E}, S_{D E F}, S_{B F D}, S_{C F D}\) и \(S_{C D E F}\) соответственно.
Треугольники \(B F D\) и \(C F D\) имеют общую высоту, проведённую из вершины \(F\); треугольники \(A B E\) и \(D B E\) равны; треугольники \(B D E\) и \(D E F\) имеют общую высоту, проведённую из вершины \(D\).
Следовательно, получаем:
\( S_{B D E}=S ; S_{\text {DEF }}=\dfrac{E F}{B E} \cdot S_{B D E}=\dfrac{S}{6} ;\)
\(S_{B F D}=S_{B D E}+S_{D E F}=S+\dfrac{S}{6}=\dfrac{7 S}{6} ; \)
\(S_{C F D}=\dfrac{C D}{B D} \cdot S_{B F D}=\)
\(\dfrac{2}{5} \cdot \dfrac{7 S}{6}=\dfrac{7 S}{15} ; S_{C D E F}=\)
\(S_{C F D}+S_{D E F}=\dfrac{7 S}{15}+\dfrac{S}{6}=\dfrac{19 S}{30}, \)
откуда \(\dfrac{S}{S_{\text {CDEF }}}=\dfrac{30}{19} \) .
Ответ
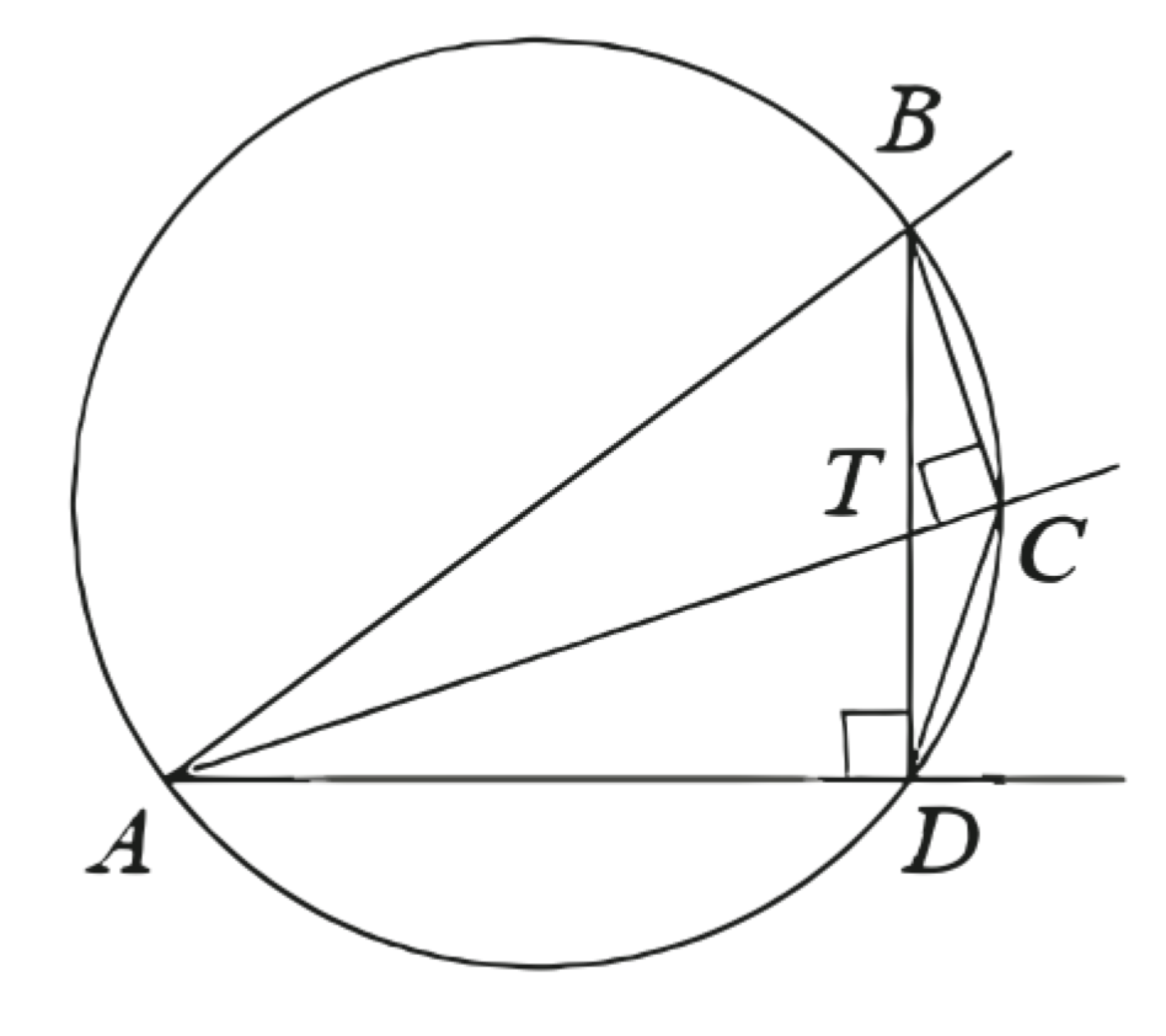
(ЕГЭ, 2022) На стороне острого угла с вершиной \(A\) отмечена точка \(B\). Из точки \(B\) на биссектрису и другую сторону угла опущены перпендикуляры \(B C\) и \(B D\) соответственно.
a) Докажите, что \(A C^2+C D^2=A D^2+B D^2\).
б) Прямые \(A C\) и \(B D\) пересекаются в точке \(T\). Найдите отношение \(A T: T C\), если \(\cos \angle A B C=\dfrac{3}{8}\).
Решение
a) Углы \(B C A\) и \(B D A\) прямые, значит, точки \(C\) и \(D\) лежат на окружности с диаметром \(A B\). Биссектриса \(A C\) вписанного угла \(B A D\) делит дугу \(B C D\) пополам, значит, хорды \(B C\) и \(C D\), стягивающие равные дуги, равны. Следовательно,
\(A C^2+C D^2=A C^2+B C^2=A B^2\)
\(=A D^2+B D^2 .\)
б) Пусть \(\angle B A C=\angle C A D=\alpha\), тогда
\begin{equation*}
\sin \alpha=\sin \angle B A C=\cos \angle A B C=\dfrac{3}{8} .
\end{equation*}
Вписанные углы, опирающиеся на одну дугу, равны, значит, \(\angle C B D=\angle C A D=\alpha ; T C=B C \cdot \operatorname{tg} \alpha\).
В прямоугольных треугольниках \(A B C, A B D\) и \(A T D\) :
\(A B=\dfrac{B C}{\sin \alpha} ; \)
\(A D=A B \cdot \cos 2 \alpha=\dfrac{B C \cdot \cos 2 \alpha}{\sin \alpha} ; \)
\(A T=\dfrac{A D}{\cos \alpha}=\dfrac{B C \cdot \cos 2 \alpha}{\sin \alpha \cdot \cos \alpha} .\)
Получаем:
\(A T: T C=\dfrac{B C \cdot \cos 2 \alpha}{\sin \alpha \cdot \cos \alpha}:(B C \cdot \operatorname{tg} \alpha)=\)
\(\dfrac{\cos 2 \alpha}{\sin ^2 \alpha}=\dfrac{1-2 \sin ^2 \alpha}{\sin ^2 \alpha}=\dfrac{46}{9} .\)
Ответ
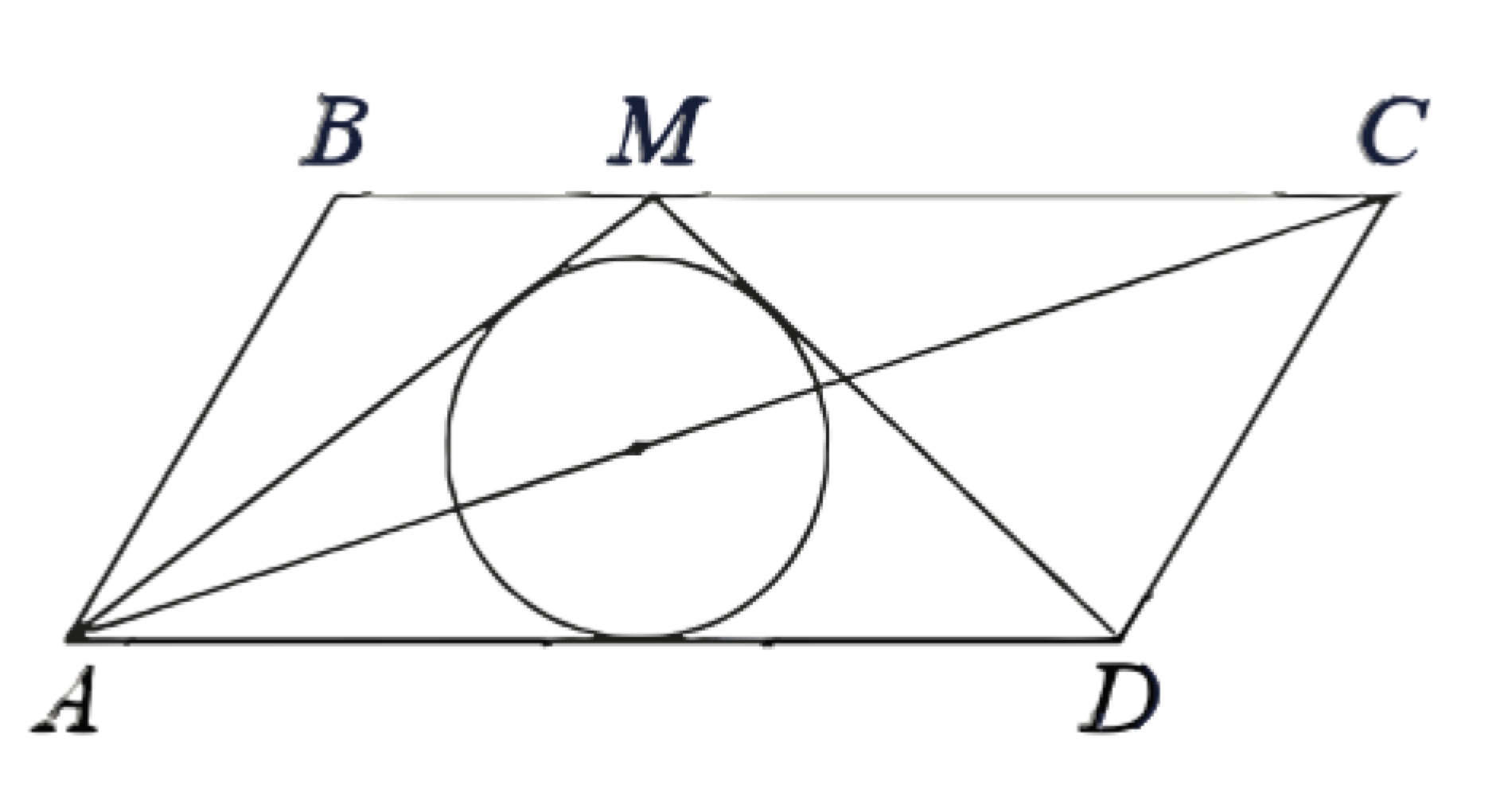
(ЕГЭ, 2022) На стороне \(B C\) параллелограмма \(A B C D\) выбрана точка \(M\) такая, что \(A M=M C\).
a) Докажите, что центр вписанной в треугольник \(A M D\) окружности лежит на диагонали \(A C\).
б) Найдите радиус вписанной в треугольник \(A M D\) окружности, если \(A B=5\), \(B C=10, \angle B A D=60^{\circ}\).
Решение
a) Треугольник \(A M C\) равнобедренный, следовательно, \(\angle M A C=\angle M C A\).
Прямые \(A D\) и \(B C\) параллельны, следовательно, накрест лежащие углы \(B C A\) и \(C A D\) при секущей \(A C\) равны.
Получаем, что \(\angle M A C=\angle M C A=\angle C A D\), а значит, луч \(A C\) является биссектрисой угла \(M A D\), на которой лежит центр вписанной в треугольник \(A M D\) окружности.
б) Обозначим \(A M=M C\) через \(x\), тогда \(B M=10-x\).
По теореме косинусов в треугольнике \(A B M\) :
\(A M^2=A B^2+B M^2-2 A B \cdot B M \cdot \cos 120^{\circ} ; \)
\(x^2=25+(10-x)^2+5(10-x),\)
откуда \(x=7\).
По теореме косинусов в треугольнике \(C M D\), в котором \(\angle M C D=60^{\circ}\),
\begin{equation*}
M D=\sqrt{M C^2+C D^2-M C \cdot C D}=\sqrt{39} .
\end{equation*}
Треугольник \(A M D\) и параллелограмм \(A B C D\) имеют общую высоту, равную расстоянию между прямыми \(A D\) и \(B C\), и общую сторону \(A D\), перпендикулярную этой высоте. Значит, площадь \(S_{A M D}\) треугольника \(A M D\) равна половине площади параллелограмма \(A B C D\) :
\begin{equation*}
S_{A M D}=\dfrac{A B \cdot A D \cdot \sin \angle B A D}{2}=\dfrac{25 \sqrt{3}}{2} .
\end{equation*}
С другой стороны, площадь треугольника \(A M D\) равна половине произведения его периметра на радиус вписанной окружности. Отсюда найдём радиус \(r\) вписанной в треугольник \(A M D\) окружности:
\(r=\dfrac{2 S_{A M D}}{A M+M D+A D}=\dfrac{25 \sqrt{3}}{7+\sqrt{39}+10}=\)
\(\dfrac{25 \sqrt{3}}{17+\sqrt{39}}=\dfrac{17 \sqrt{3}-3 \sqrt{13}}{10} .\)
Ответ
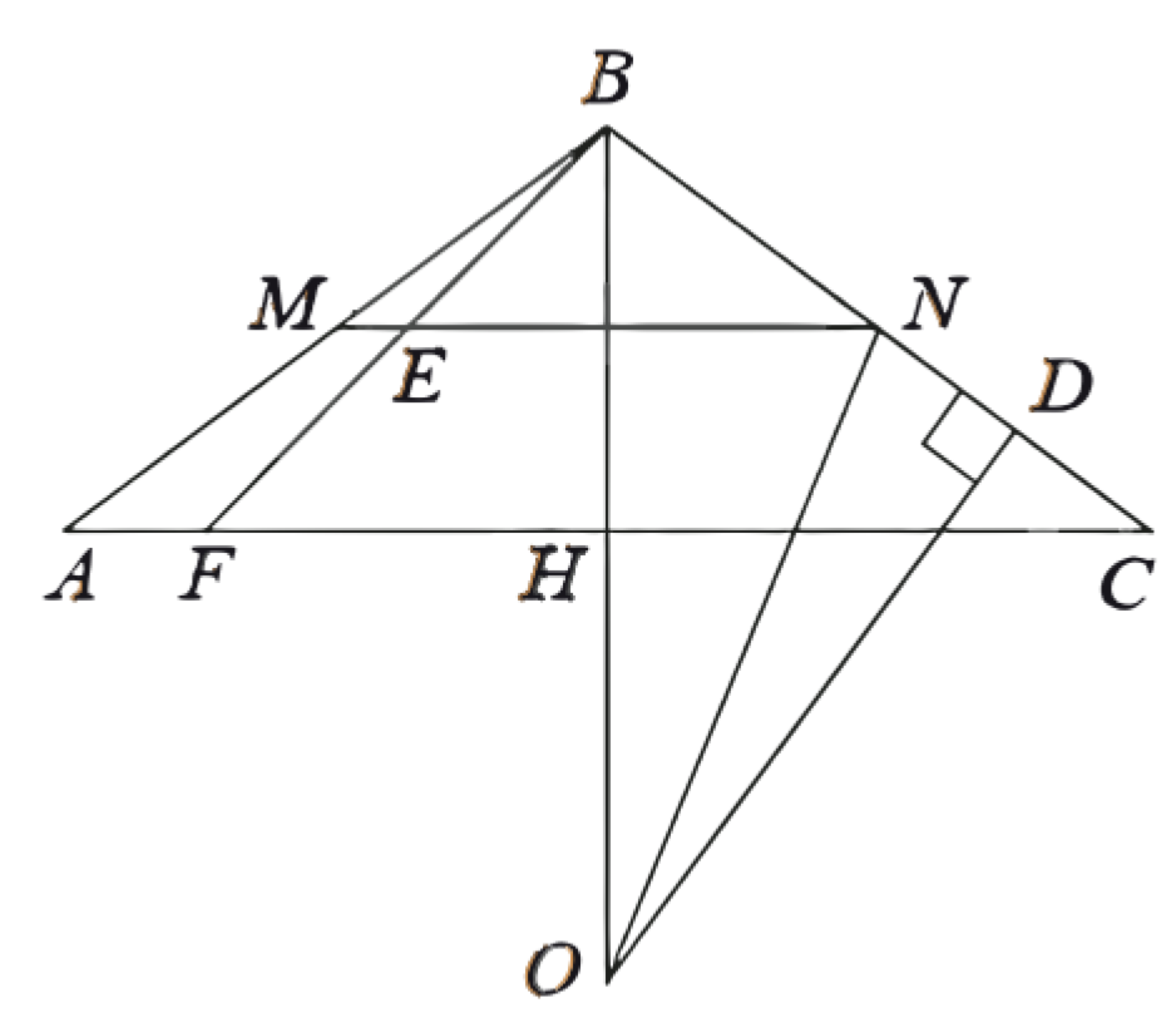
(ЕГЭ, 2022) В треугольнике \(A B C\) точки \(M\) и \(N\) - середины сторон \(A B\) и \(B C\) соответственно. Известно, что около четырёхугольника \(A M N C\) можно описать окружность.
a) Докажите, что треугольник \(A B C\) равнобедренный.
б) На стороне \(A C\) отмечена точка \(F\) такая, что \(\angle A F B=135^{\circ}\). Отрезок \(B F\) пересекает отрезок \(M N\) в точке \(E\). Найдите радиус окружности, описанной около четырёхугольника \(A M N C\), если \(\angle A B C=120^{\circ}, E F=6 \sqrt{2}\).
Решение
a) Отрезок \(M N\) - средняя линия треугольника \(A B C\), значит, прямые \(A C\) и \(M N\) параллельны, а четырёхугольник \(A M N C\) является трапецией \((M N<A C)\).
Поскольку окружность можно описать только около равнобедренной трапеции, \(A M=C N\), то есть \(A B=B C\), а значит, треугольник \(A B C\) равнобедренный.
б) Пусть точка \(O\) - центр окружности, описанной около трапеции \(A M N C\), точка \(H\) - основание высоты \(B H\) треугольника \(A B C\), а точка \(D-\) середина отрезка \(N C\).
Угол \(E F C\) равен \(45^{\circ}\), значит, расстояние между прямыми \(A C\) и \(M N\) равно \(E F \cdot \sin 45^{\circ}=6\).
Поскольку отрезок \(M N-\) средняя линия треугольника \(A B C\), он делит высоту \(B H\) пополам, значит, \(B H=12\).
Треугольник \(A B C\) равнобедренный, поэтому \(\angle B C A=\angle B A C=\dfrac{180^{\circ}-\angle A B C}{2}=30^{\circ}\).
В прямоугольном треугольнике \(B C H\) угол \(C\) равен \(30^{\circ}\), значит,
\(B C=2 B H=24 ; B N=\dfrac{B C}{2}=12,\)
\(N D=\dfrac{B C}{4}=6, B D=B N+N D=18 \text {. }\)
Центр описанной около многоугольника окружности лежит на пересечении серединных перпендикуляров к каждой из его сторон, следовательно, \(\angle B D O=90^{\circ}\), точка \(H\) лежит на прямой \(B O\), а \(N O\) - радиус окружности, описанной около четырёхугольника \(A M N C\).
В прямоугольном треугольнике \(B D O\) угол \(O B D\) равен \(60^{\circ}\), откуда находим \(O D=B D \cdot \operatorname{tg} 60^{\circ}=18 \sqrt{3}\).
Из прямоугольного треугольника \(N D O\) находим \(O N=\sqrt{O D^2+N D^2}=12 \sqrt{7}\).