17. Планиметрия
Чтобы получить дополнительный функционал нужно войти.
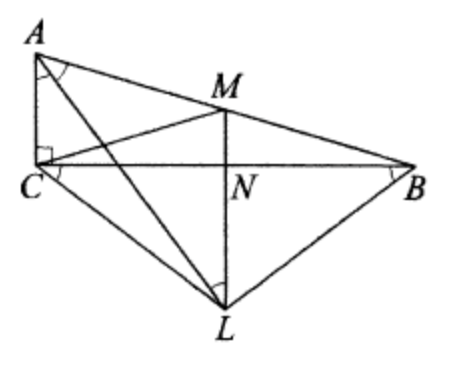
(ЕГЭ,2016) В прямоугольном треугольнике \(A B C\) точки \(M\) и \(N\) - середины гипотенузы \(A B\) и катета \(B C\) соответственно. Биссектриса угла \(B A C\) пересекает прямую \(M N\) в точке \(L\).
a) Докажите, что треугольники \(A M L\) и \(B L C\) подобны.
б) Найдите отношение площадей этих треугольников, если \(\cos \angle B A C=\frac{7}{25}\).
Решение
a) Прямая \(M L\) параллельна прямой \(A C\), так как содержит среднюю линию треутольника \(A B C\) (см. рисунок). Следовательно,
\begin{equation*}
\angle A L M=\angle L A C=\angle L A M \text {. }
\end{equation*}
Таким образом,
\begin{equation*}
L M=A M=B M=C M,
\end{equation*}
то есть точки \(A, B, C\) и \(L\) лежат на окружности с центром в точке \(M\). Получаем:
\begin{equation*}
\angle L B C=\angle L A C=\angle L A B=\angle L C B,
\end{equation*} а значит, треугольники \(A M L\) и \(B L C\) подобны по двум углам.
б) Углы \(A L B\) и \(A C B\) опираются на одну дугу, значит, \(\angle A L B=90^{\circ}\). Коэффициент подобия треугольников \(B L C\) и \(A M L\) равен
\begin{equation*}
\frac{L B}{A M}=\frac{2 L B}{A B}=2 \sin \angle L A B \text {. }
\end{equation*}
По условию
\begin{equation*}
\cos \angle B A C=\frac{7}{25},
\end{equation*}
откуда
\begin{equation*}
1-2 \sin ^2 \angle B A L=\frac{7}{25} ; \sin ^2 \angle B A L=\frac{9}{25} ; \sin \angle B A L=\frac{3}{5} .
\end{equation*}
Значит, \(\frac{A M}{L B}=\frac{5}{6}\) и площади треугольников \(A M L\) и \(B L C\) относятся как \(\frac{25}{36}\).
Ответ
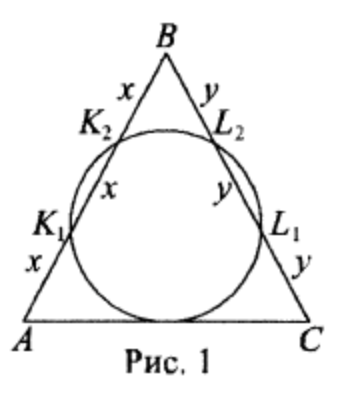
(ЕГЭ,2016) Окружность касается стороны \(A C\) остроугольного треугольника \(A B C\) и делит каждую из сторон \(A B\) и \(B C\) на три равные части.
a) Докажите, что треугольник \(A B C\) равнобедренный.
б) Найдите, в каком отношении высота этого треутольника делит сторону \(B C\).
Решение
a) Пусть окружность делит сторону \(A B\) на три равные части (рис. 1)
\begin{equation*}
A K_1=K_1 K_2=K_2 B=x
\end{equation*}
и делит сторону \(B C\) на три равные части
\begin{equation*}
C L_1=L_1 L_2=L_2 B=y .
\end{equation*}
Тогда по свойству секущих
\begin{equation*}
B K_1 \cdot B K_2=B L_1 \cdot B L_2 ; 2 x^2=2 y^2 ; x=y,
\end{equation*}
откуда получаем:
\begin{equation*}
A B=B C .
\end{equation*}
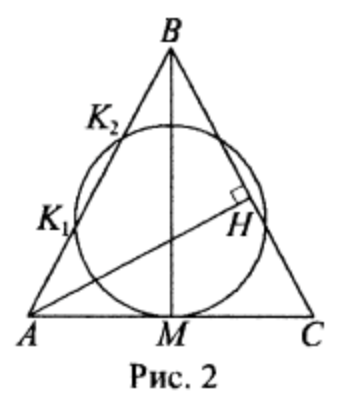
б) Пусть охружность касается стороны \(A C\) треугольника \(A B C\) в точке \(M\) (рис. 2).
Поскольку
\begin{equation*}
A M^2=A K_1 \cdot A K_2=2 x^2 \text {, }
\end{equation*}
получаем:
\begin{equation*}
A M=M C=x \sqrt{2} .
\end{equation*}
Пусть \(A H\) - высота треугольника, тогда
\begin{equation*}
\begin{gathered}
H C=A C \cdot \cos \angle A C B=\frac{A C \cdot M C}{B C}=\frac{4}{3} x ; \\
B H=B C-H C=\frac{5}{3} x
\end{gathered}
\end{equation*}
Таким образом, \(B H: H C=5: 4\).
Ответ
(ЕГЭ,2016) В прямоугольном треугольнике \(ABC\) с прямым углом \(C\) точки \(M\) и \(N\) - середины катетов \(AC\) и \(BC\) соответственно, \(CH\) - высота.
а) Докажите, что прямые \(MH\) и \(NH\) перпендикулярны
б) Пусть \(P\) - точка пересечения прямых \(AC\) и \(NH\), а \(Q\) - точка пересечения прямых \(BC\) и \(MH\). Найдите площадь треугольника \(PQM\), если \(AH=4\) и \(BH=2\)
Решение
a) Треугольники \(A I I C\) и \(B H C\) прямоугольные,
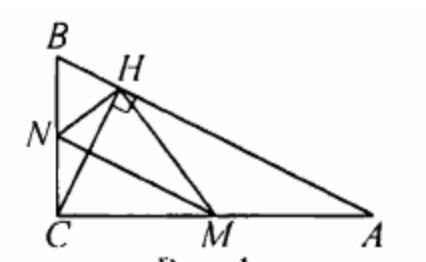
поэтому \(M H=\frac{A C}{2}=C M\) и \(N H=\frac{C B}{2}=C N\). Значит, треугольники \(M C N\) и \(M H N\) равны по трём сторонам, откуда \(\angle M H N=\angle M C N=90^{\circ}\).
б) В прямоугольном треугольнике \(A B C\) имеем: \(C H=\sqrt{A H \cdot B H}=2 \sqrt{2}\).
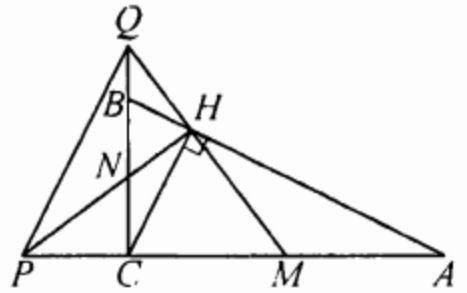
В прямоугольных треугольниках \(M H P\) и \(M C Q\) с общим углом \(C M H\) получаем:
\begin{equation*}
\frac{M H}{M P}=\frac{M C}{M Q}=\cos \angle C M H,
\end{equation*}
поэтому треугольники \(M H C\) и \(M P Q\) подобны с коэффициентом подобия \(\cos \angle C M H\).
Площадь \(S\) треугольника \(M H C\) равна половине площади треугольника \(A H C\), то есть \(S=\frac{A H \cdot C H}{4}=2 \sqrt{2}\).
Найдём \(\cos \angle C M H\) :
\begin{equation*}
\begin{gathered}
\cos \angle C M H=\cos (2 \angle C A H)=2 \cos ^2 \angle C A H-1= \\
=\frac{2 A H^2}{A C^2}-1=\frac{2 A H^2}{A H^2+C H^2}-1=\frac{1}{3} .
\end{gathered}
\end{equation*}
Значит, площадь треугольника \(M P Q\) равна \(\frac{S}{\cos ^2 \angle C M H}=18 \sqrt{2}\).
Ответ
(ЕГЭ,2016) На катетах \(A C\) и \(B C\) прямоугольного треугольника \(A B C\) как на диаметрах построены окружности, второй раз пересекающиеся в точке \(M\). Точка \(Q\) лежит на меньшей дуге \(M B\) окружности с диаметром \(B C\). Прямая \(C Q\) второй раз пересекает окружность с диаметром \(A C\) в точке \(P\).
a) Докажите, что прямые \(P M\) и \(Q M\) перпендикулярны.
б) Найдите \(P Q\), если \(A M=1, B M=3\), а \(Q\) - середина дуги \(M B\).
Решение
a) Поскольку \(\angle A M C=\angle B M C=90^{\circ}\), точки \(M, A\) и \(B\) лежат на одной прямой, значит, отрезок \(C M\) высота треугольника \(A B C\) (см. рисунок).
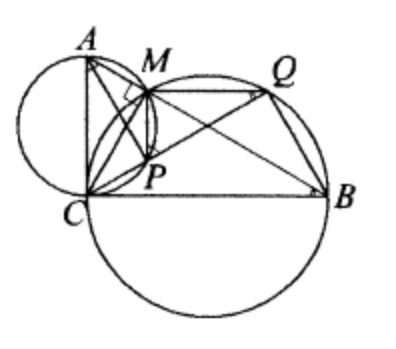
Четырёхугольники \(A M P C\) и \(B Q M C\) вписаны в окружности, позтому
\begin{equation*}
\begin{aligned}
\angle Q P M= & 180^{\circ}-\angle C P M=\angle M A C=90^{\circ}-\angle M B C= \\
& =90^{\circ}-\angle M Q C=90^{\circ}-\angle M Q P,
\end{aligned}
\end{equation*}
откуда \(\angle P M Q=90^{\circ}\).
б) Из прямоугольного треугольника \(A B C\) получаем:
\begin{equation*}
C M=\sqrt{A M B M}=\sqrt{3},
\end{equation*}
откуда
\begin{equation*}
\angle B A C=\angle B C M=60^{\circ}, \angle A B C=\angle A C M=30^{\circ} .
\end{equation*}
Точка \(Q\) - середина дути \(M B\), поэтому \(C Q\) - биссектриса угла \(B C M\).
Значит,
\begin{equation*}
\begin{gathered}
\angle A C M=\angle M C Q=\angle Q C B=30^{\circ} ; \\
\angle C A P=\angle C A M-\angle P A M=\angle B A C-\angle M C P=30^{\circ}=\angle A C M ; \\
\angle Q B C=\angle Q B M+\angle M B C=\angle Q C M+\angle A B C=60^{\circ}=\angle M C B
\end{gathered}
\end{equation*}
Получаем:
\begin{equation*}
C Q=B M=3 \text { и } C P=A M=1
\end{equation*}
как хорды, стягивающие равные дуги.
Таким образом, \(P Q=C Q-C P=2\).
