17. Планиметрия
Чтобы получить дополнительный функционал нужно войти.
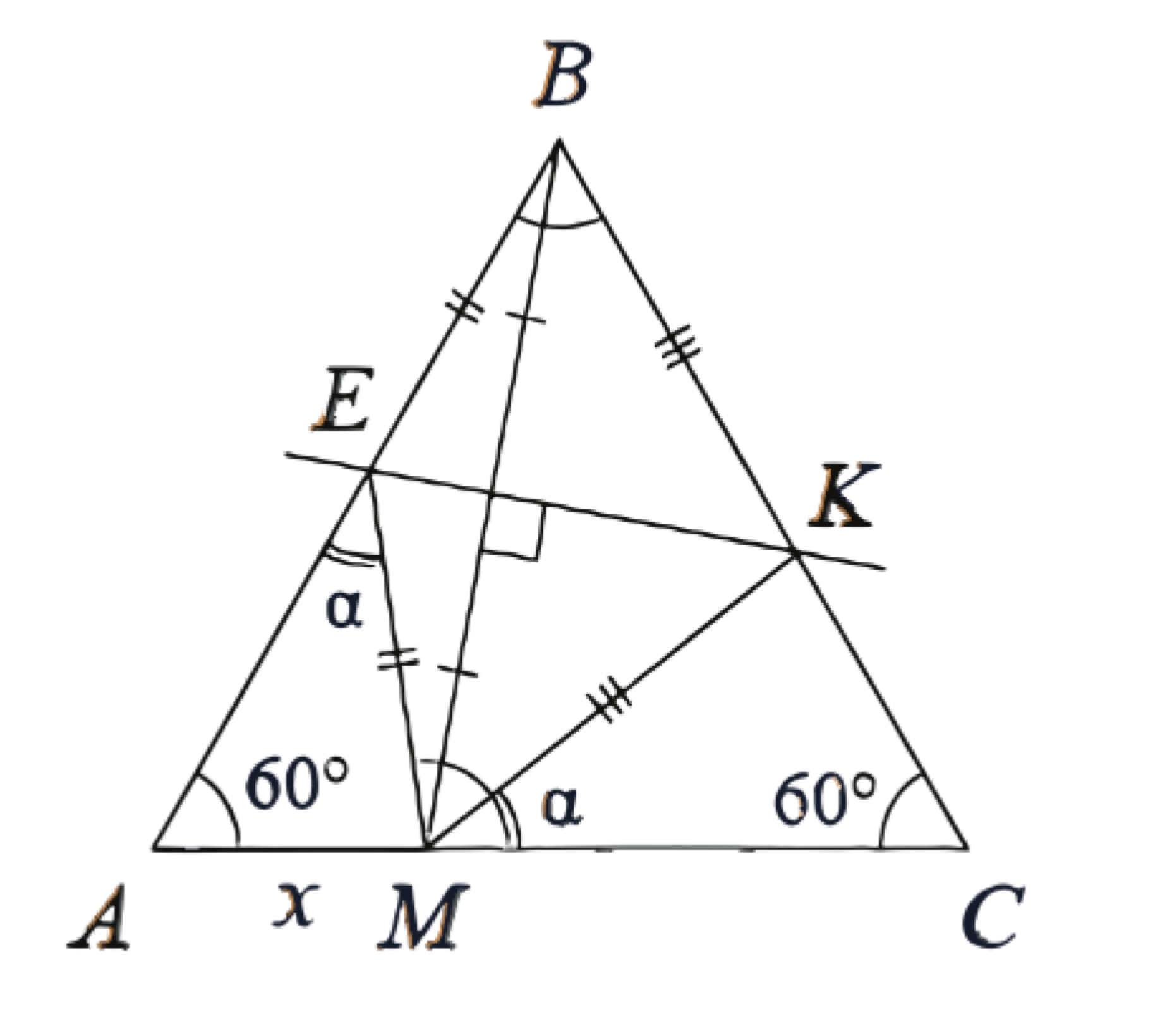
(ЕГЭ, 2023) На стороне \(A C\) равностороннего треугольника \(A B C\) отмечена точка \(M\). Серединный перпендикуляр к отрезку \(B M\) пересекает стороны \(A B\) и \(B C\) в точках \(E\) и \(K\) соответственно.
a) Докажите, что \(\angle A E M=\angle C M K\).
б) Найдите отношение площадей треугольников \(A E M\) и \(C M K\), если \(A M: M C=1: 4\).
Решение
a) Треугольники \(M E B\) и \(M K B\) равнобедренные.
Значит, \( \angle E M B=\angle E B M, \quad \angle K M B=\angle K B M\).
Следовательно, \(\angle E M K=\angle E B K=60^{\circ}\).
Пусть \(\angle A E M=\alpha\). Тогда:
\begin{equation*}
\begin{gathered}
\angle E M A=180^{\circ}-\angle E A M-\alpha=120^{\circ}-\alpha ; \\
\angle C M K=180^{\circ}-\angle E M A-\angle E M K= \\
=180^{\circ}-\left(120^{\circ}-\alpha\right)-60^{\circ}=\alpha .
\end{gathered}
\end{equation*}
б) Пусть \( A M=x . \) Тогда \( M C=4 x, A B=B C=A C=5 x \)
Периметр треугольника \(A E M\) равен
\(A M+A E+E M=A M+A E+E B=\)
\(=A M+A B=6 x.\)
Периметр треугольника \(C M K\) равен
\(C M+C K+M K=C M+C K+K B=\)
\(=C M+B C=9 x.\)
Треугольники \(A E M\) и \(C M K\) подобны по двум углам. Отношение их периметров равно \(\dfrac{2}{3}\), значит, коэффициент подобия равен \(\dfrac{2}{3}\). Следовательно, отношение площадей треугольников \(A E M\) и \(C M K\) равно \(\dfrac{4}{9}\).
Ответ
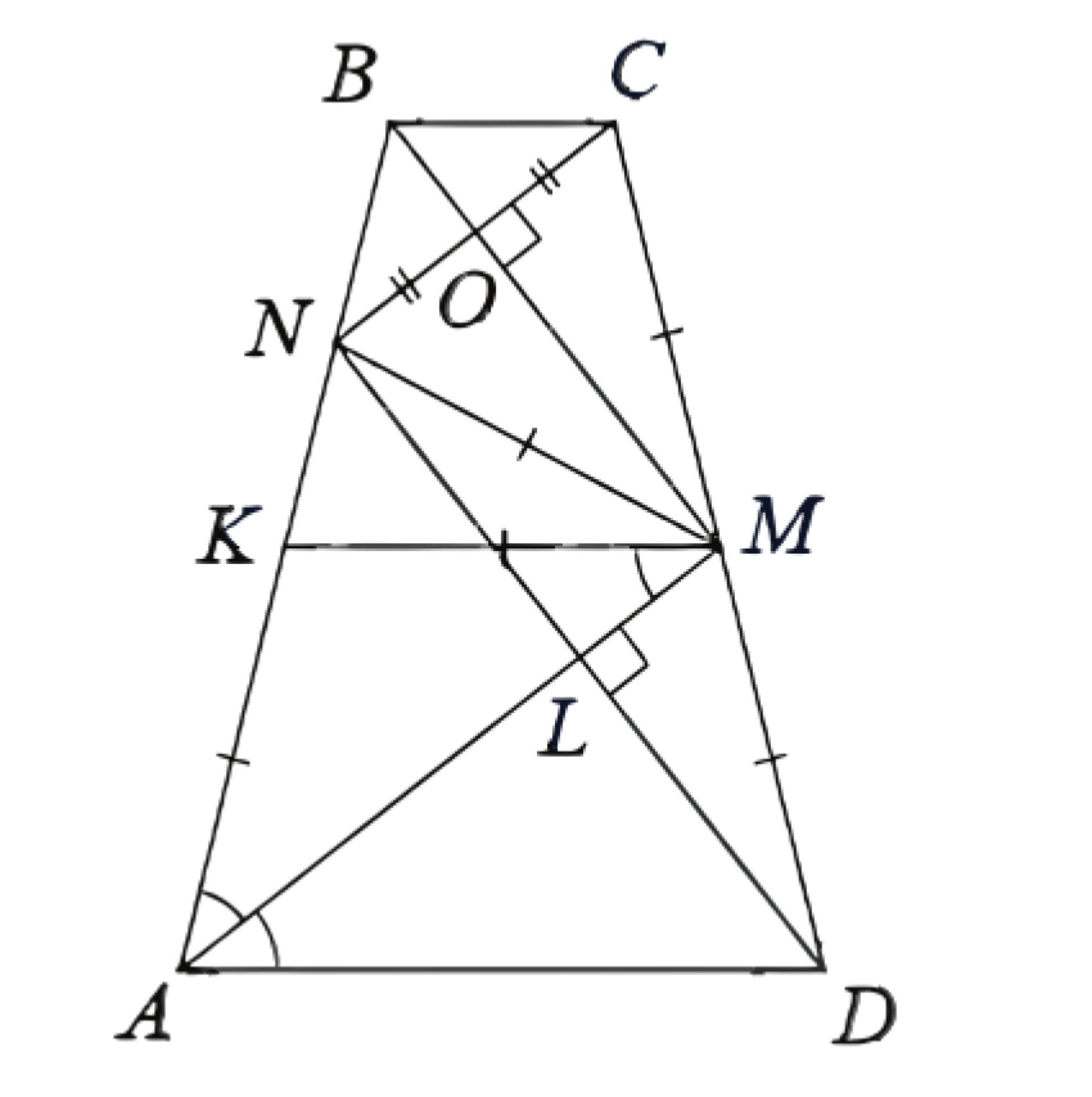
(ЕГЭ, 2023) Биссектриса \(A M\) острого угла \(A\) равнобедренной трапеции \(A B C D\) делит боковую сторону \(C D\) пополам. Отрезок \(D N\) перпендикулярен отрезку \(A M\) и делит сторону \(A B\) в отношении \(A N:N B=5: 1\).
a) Докажите, что прямые \(B M\) и \(C N\) перпендикулярны.
б) Найдите длину отрезка \(M N\), если площадь трапеции равна \(3 \sqrt{2}\).
Решение
a) Пусть \(K M\) - средняя линия трапеции \(A B C D\), отрезки \(A M\) и \(D N\) пересекаются в точке \(L\), отрезки \(B M\) и \(C N\) пересекаются в точке \(O\).
Поскольку прямые \(K M\) и \(A D\) параллельны и \(A M\) - биссектриса, получаем:
\begin{equation*}
{\angle K M A=\angle M A D=\angle K A M}
\end{equation*}
Таким \(\quad\) образом, \(\quad\) треугольник \(A K M\) равнобедренный и \(K M=K A=\dfrac{1}{2} A B\).
Следовательно, треугольник \(A M B\) прямоугольный, \(\angle A M B=90^{\circ}\).
Поскольку \(A L\) является биссектрисой и высотой в треугольнике \(A N D\), этот треугольник равнобедренный и точка \(L\) - середина отрезка \(N D\).
Средняя линия \(M L\) в треугольнике \(C N D\) перпендикулярна отрезку \(N D\), значит, \(\angle C N D=90^{\circ}\).
Поскольку в четырёхугольнике \(N L M O\) три угла прямые, оставшийся угол тоже прямой, то есть прямые \(B M\) и \(C N\) перпендикулярны.
б) Пусть \(B N=x\). Тогда: \(A D=A N=5 x ; \quad C D=A B=6 x ; \quad\)
\(K M=\dfrac{1}{2} A B=3 x\); \(B C=2 K M-A D=x\).
Высота трапеции равна
\(h=\sqrt{A B^2-\left(\dfrac{A D-B C}{2}\right)^2}=\)
\(\sqrt{36 x^2-4 x^2}=4 x \sqrt{2},\)
а её площадь равна
\(h \cdot \dfrac{B C+A D}{2}=4 x \sqrt{2} \cdot 3 x=12 \sqrt{2} \cdot x^2=\)
\(3 \sqrt{2},\)
откуда \(x^2=\dfrac{1}{4} ; x=\dfrac{1}{2}\).
Отрезок \(M N\) является медианой в прямоугольном треугольнике \(C N D\), проведённой из вершины прямого угла. Следовательно, \(M N=\dfrac{C D}{2}=3 x=\dfrac{3}{2}\).
Ответ
(ЕГЭ, 2023) Стороны \(A B\) и \(A D\) квадрата \(A B C D\) касаются окружности, радиус которой втрое меньше стороны квадрата.
a) Докажите, что эта окружность разбивает диагональ \(B D\) на три равных отрезка.
б) Касательная к окружности, проведённая через точку \(B\), пересекает сторону \(C D\) в точке \(E\). Найдите длину отрезка \(D E\), если сторона квадрата равна 18.
Решение
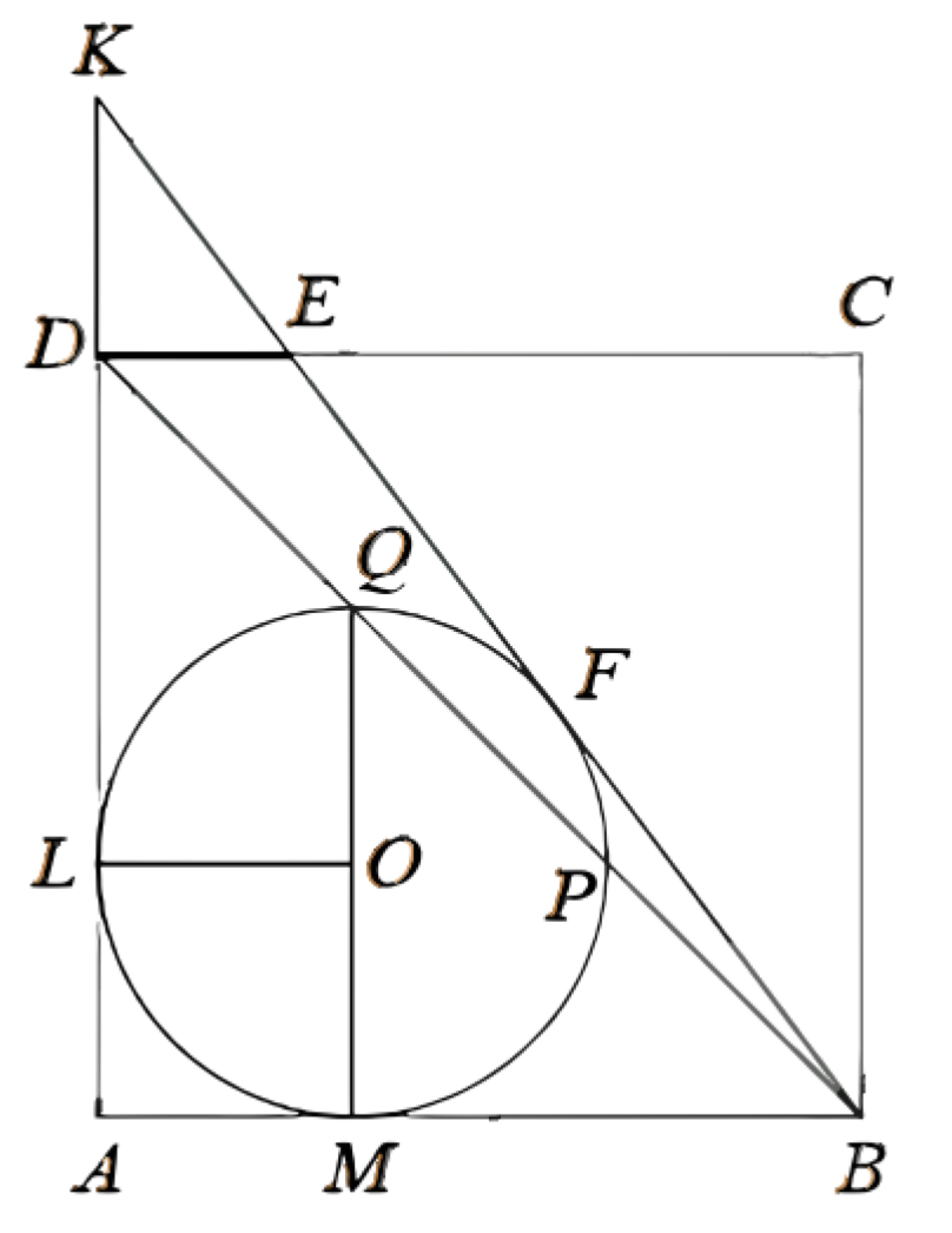
a) Пусть окружность радиусом \(R\) касается стороны \(A B\) в точке \(M\) и стороны \(A D\) в точке \(L\). Точка \(Q\), диаметрально противоположная точке \(M\), удалена от \(A B\) на расстояние \(2 R\), удалена от \(C D\) на \(A D-2 R=R\) и удалена от \(A D\) на \(R\). Точка \(Q\) равноудалена от сторон \(A D\) и \(C D\) квадрата \(A B C D\), значит, точка \(Q\) лежит на диагонали \(B D\) и делит её в отношении \(1: 2\), считая от \(D\).
Аналогично точка \(P\), диаметрально противоположная точке \(L\), лежит на диагонали \(B D\) и делит её в отношении \(1: 2\), считая от \(B\).
Следовательно, \(B P=D Q=P Q\).
б) Пусть окружность касается прямой \(B E\) в точке \(F\). Продолжим \(B E\) до пересечения с прямой \(A D\) в точке \(K\). Пусть \(K F=K L=x\). Тогда
\(A K=A L+K L=6+x \text { и } K B=\)
\(B F+K F=B M+K F=12+x .\)
По теореме Пифагора:
\begin{equation*}
B K^2=A B^2+A K^2 ;(12+x)^2=18^2+(6+x)^2
\end{equation*}
откуда \(x=18\). Значит, \(D K=x-12=6\).
Прямоугольные треугольники \(E D K\) и \(E C B\) подобны с коэффициентом \(\dfrac{D K}{B C}=\dfrac{6}{18}=\dfrac{1}{3}\), следовательно,
\begin{equation*}
D E=\dfrac{1}{3} C E=\dfrac{1}{4} C D=\dfrac{1}{4} \cdot 18=\dfrac{9}{2} .
\end{equation*}
Ответ
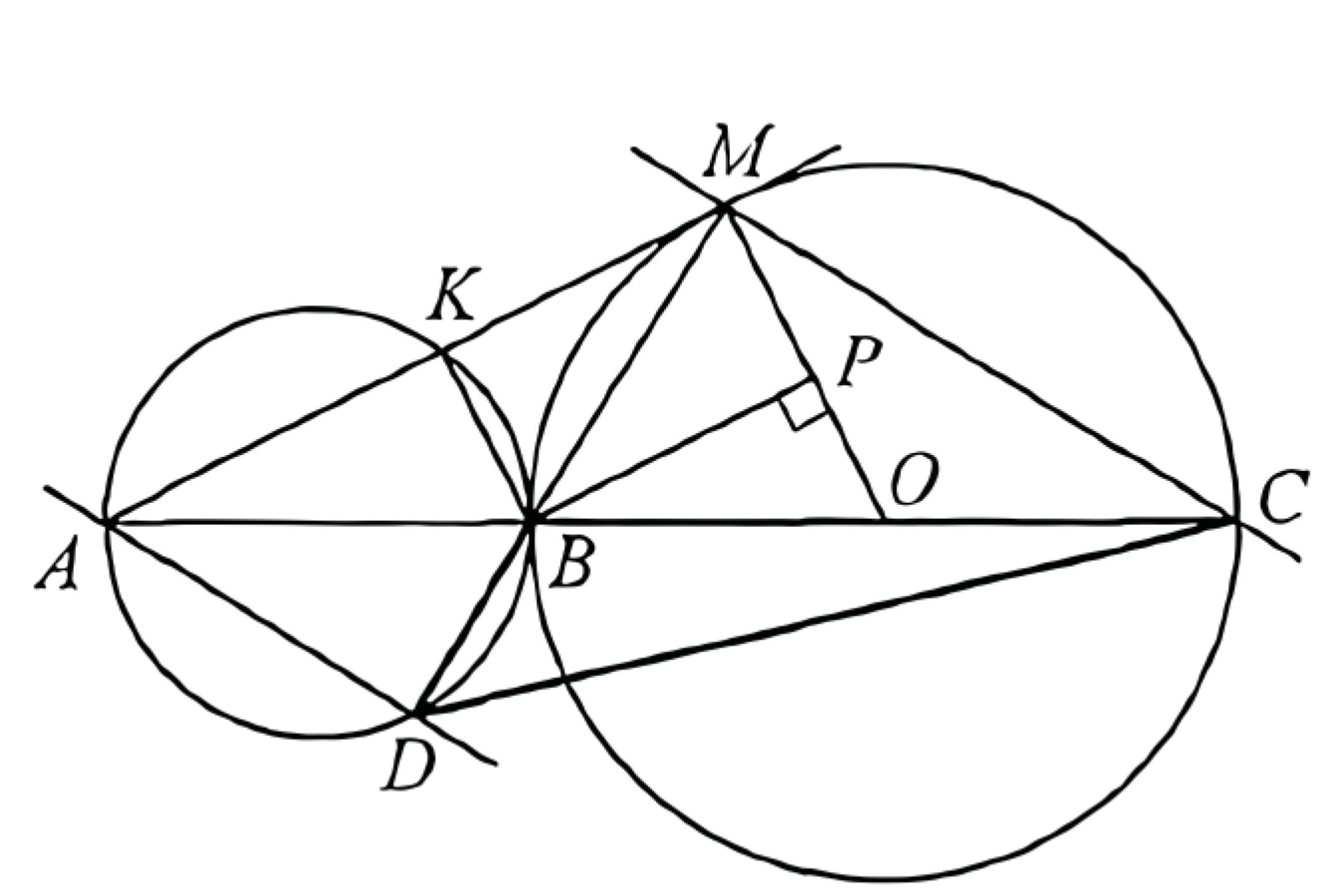
(ЕГЭ, 2023) Точка \(B\) лежит на отрезке \(A C\). Прямая, проходящая через точку \(A\), касается окружности с диаметром \(B C\) в точке \(M\) и второй раз пересекает окружность с диаметром \(A B\) в точке \(K\). Продолжение отрезка \(M B\) пересекает окружность с диаметром \(A B\) в точке \(D\).
a) Докажите, что прямые \(A D\) и \(M C\) параллельны.
б) Найдите площадь треугольника \(D B C\), если \(A K=5\) и \(M K=25\).
Решение
a) Точки \(M\) и \(D\) лежат на окружностях с диаметрами \(B C\) и \(A B\) соответственно, поэтому
\begin{equation*}
\angle B M C=\angle B D A=90^{\circ} \text {. }
\end{equation*}
Прямые \(A D\) и \(M C\)
перпендикулярны одной и той же прямой \(M D\), следовательно, прямые \(A D\) и \(M C\) параллельны.
б) Пусть \(O\) - центр окружности с диаметром \(B C\). Тогда прямые \(O M\) и \(A M\) перпендикулярны. Учитывая, что прямые \(B K\) и \(A M\) перпендикулярны, получаем, что прямые \(O M\) и \(B K\) параллельны.
Обозначим \(B K\) через \(x\). Треугольник \(A M O\) подобен треугольнику \(A K B\) с коэффициентом 6 , поэтому \(O B=O M=6 x\).
Опустим перпендикуляр \(B P\) из точки \(B\) на прямую \(O M\). Так как четырёхугольник \(B K M P\) - прямоугольник, то
\(B P=K M=25, O P=O M-M P=\)
\(=O M-B K=6 x-x=5 x\)
По теореме Пифагора \(O B^2=B P^2+O P^2\), откуда \(36 x^2=625+25 x^2\). Получаем, что \(x=\dfrac{25}{\sqrt{11}}\).
Поскольку прямые \(A D\) и \(M C\) параллельны,
\(S_{D B C}=S_{M D C}-S_{M B C}=S_{M A C}-S_{M B C}=\)
\(=S_{A B M} .\)
Значит, треугольники \(D B C\) и \(A M B\) равновелики. Следовательно,
\(S_{D B C}=S_{A M B}=\dfrac{1}{2} A M \cdot B K=\dfrac{1}{2} \cdot 30 x=\)
\(\dfrac{1}{2} \cdot 30 \cdot \dfrac{25}{\sqrt{11}}=\dfrac{375 \sqrt{11}}{11} .\)
Ответ
(ЕГЭ, 2023) Прямая, перпендикулярная стороне \(B C\) ромба \(A B C D\), пересекает его диагональ \(A C\) в точке \(M\), а диагональ \(B D\) в точке \(N\), причём \(A M: M C=1: 2, B N: N D=1: 3\).
a) Докажите, что прямая \(M N\) делит сторону ромба \(B C\) в отношении \(1:4\).
б) Найдите сторону ромба, если \(M N=2 \sqrt{3}\).
Решение
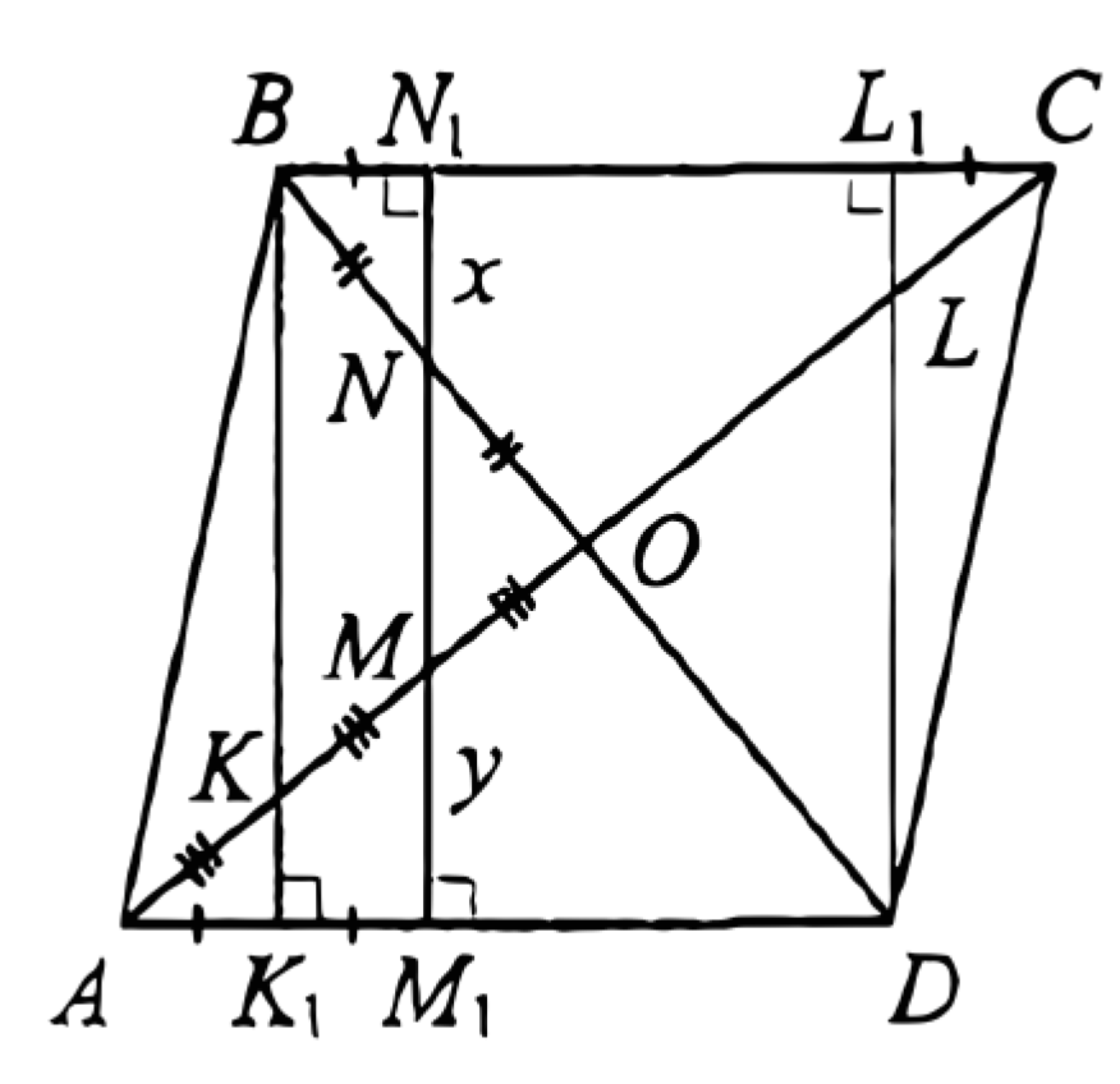
a) Пусть отрезки \(B K_1, N_1 M_1, L_1 D\) - высоты ромба, причём \(N_1 M_1\) проходит через точки \(M\) и \(N\). Тогда \(B N_1: N_1 L_1=B N: N D=1: 3\). Диагонали \(B D\) и \(A C\) пересекаются в точке \(O\).
Пусть высоты \(B K_1\) и \(L_1 D\) пересекают диагональ \(A C\) в точках \(K\) и \(L\) соответственно. Поскольку \(B N=N O\) и прямые \(B K\) и \(N M\) параллельны, получаем: \(K M=M O=\dfrac{1}{6} A C\), а значит, \(A K=K M\).
Таким образом, \(A K_1=K_1 M_1=B N_1\), но \(A K_1=L_1 C\), поэтому \(B N_1=L_1 C\). Следовательно, \(B N_1: N_1 C=B N_1:\left(N_1 L_1+L_1 C\right)=1: 4\).
б) Пусть \(N N_1=x, M M_1=y\). Тогда \(B K=2 N M=4 \sqrt{3}, \quad K K_1=\dfrac{1}{2} M M_1=\dfrac{y}{2}\), \(D L_1=4 N N_1=4 x\).
Поскольку \(B K_1=N_1 M_1=L_1 D\), получаем:
\begin{equation*}
4 \sqrt{3}+\dfrac{y}{2}=x+2 \sqrt{3}+y=4 x,
\end{equation*}
откуда находим \(x=\dfrac{6 \sqrt{3}}{5}, y=\dfrac{8 \sqrt{3}}{5} ; D L_1=\dfrac{24 \sqrt{3}}{5}\).
В прямоугольном треугольнике \(A B K_1\) имеем: \(A K_1=\dfrac{1}{5} A D=\dfrac{1}{5} A B\).
По теореме Пифагора
\(B K_1=\sqrt{A B^2-A K_1^2}=\sqrt{A B^2-\dfrac{1}{25} A B^2}=\)
\(=\dfrac{2 \sqrt{6}}{5} \cdot A B=\dfrac{24 \sqrt{3}}{5},\)
откуда \(A B=6 \sqrt{2}\).
Ответ
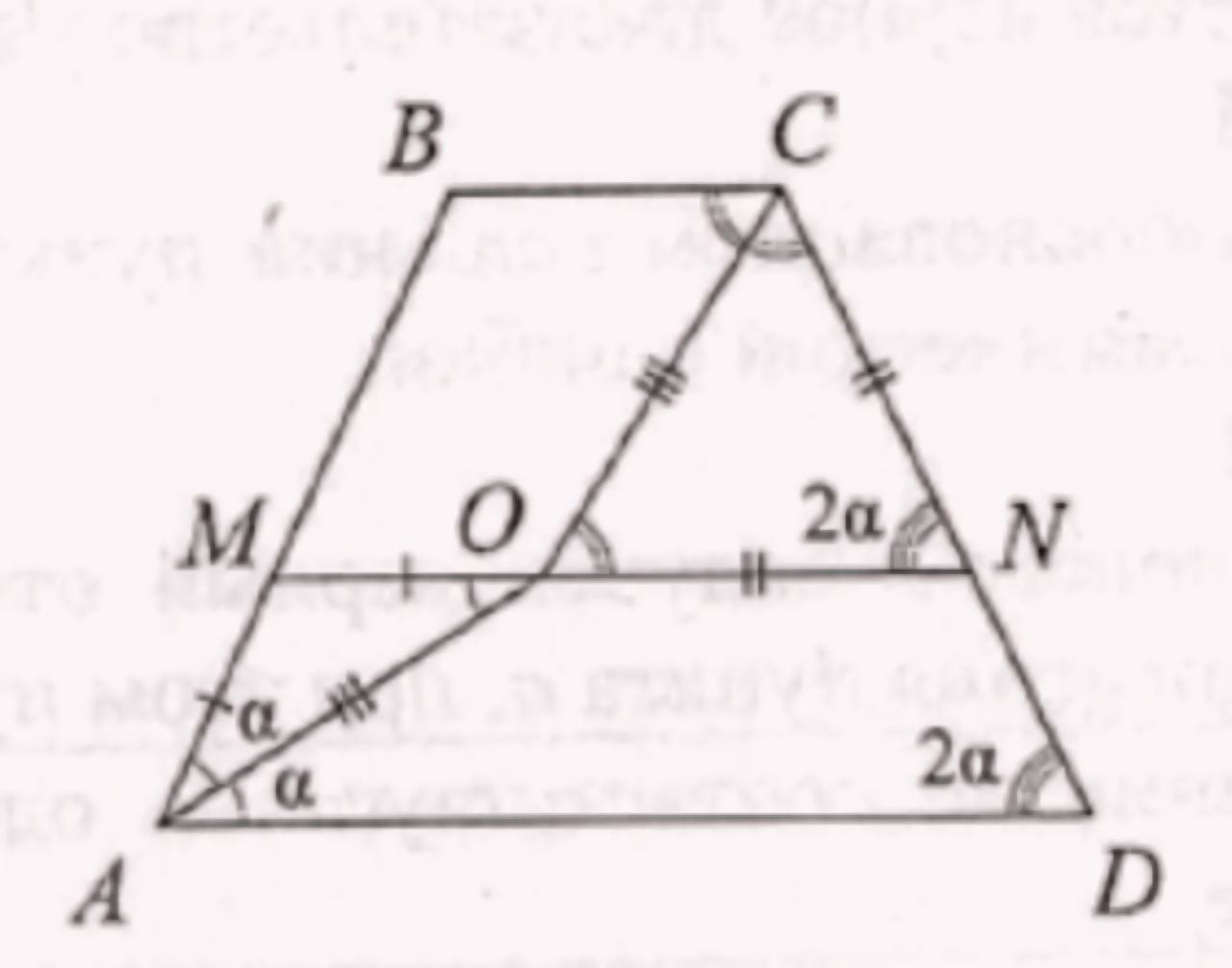
(ЕГЭ, 2023) Биссектрисы углов \(B A D\) и \(B C D\) равнобедренной трапеции \(A B C D\) пересекаются в точке \(O\). На боковых сторонах \(A B\) и \(C D\) отмечены точки \(M\) и \(N\) соответственно так, что \(A M=M O, C N=N O\).
a) Докажите, что точки \(M, O\) и \(N\) лежат на одной прямой.
б) Найдите отношение \(A M: M B\), если \(A O=C O\) и \(B C: A D=1: 7\).
Решение
a) Треугольник \(A M O\) равнобедренный (рис. 1). Следовательно,
\begin{equation*}
\angle M O A=\angle M A O=\angle D A O \text {. }
\end{equation*}
Значит, прямые \(M O\) и \(A D\) параллельны. Аналогично прямые \(N O\) и \(A D\) параллельны.
Таким образом, точки \(M, O\) и \(N\) лежат на одной прямой, параллельной \(A D\).
б) Пусть \(\angle O A D=\angle O A M=\alpha\). Тогда \(\angle C N O=\angle C D A=\angle B A D=2 \alpha \text {. }\)
Пусть \(M O=A M=a, M B=C N=O N=b\).
По теореме косинусов для треугольников \(A M O\) и \(C N O\) имеем:
\begin{equation*}
\begin{gathered}
A O^2=a^2+a^2-2 a^2 \cdot \cos \left(180^{\circ}-2 \alpha\right), \\
O C^2=b^2+b^2-2 b^2 \cdot \cos 2 \alpha,
\end{gathered}
\end{equation*}
откуда получаем:
\(a^2+a^2 \cdot \cos 2 \alpha=b^2-b^2 \cdot \cos 2 \alpha ;\)
\(\cos 2 \alpha=\dfrac{b^2-a^2}{a^2+b^2} .\)
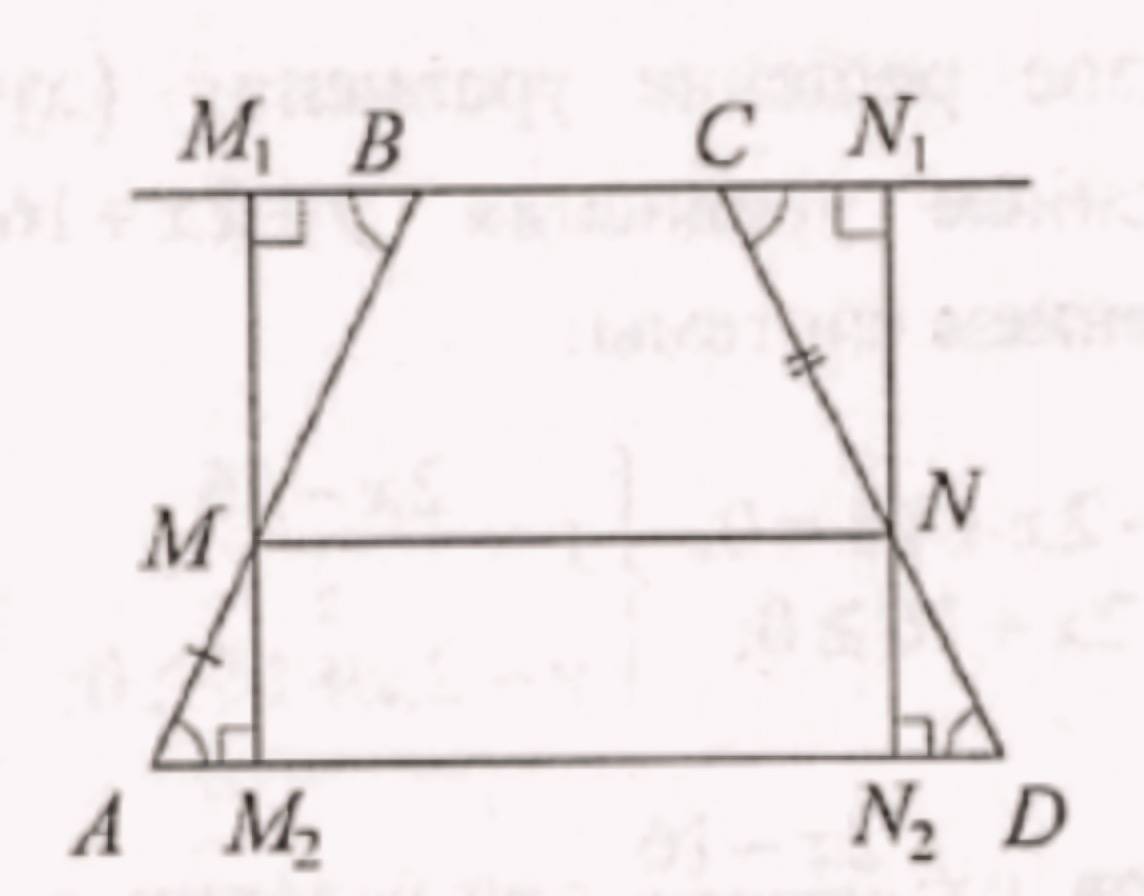
Проведём высоты \(M_1 M_2\) и \(N_1 N_2\) через точки \(M\) и \(N\) соответственно (рис. 2) и найдём длины оснований трапеции:
\(A D=A M_2+M_2 N_2+N_2 D=\)
\(=M N+2 A M \cdot \cos 2 \alpha= \)
\(=a+b+2 a \cdot \dfrac{b^2-a^2}{a^2+b^2}=\)
\(\dfrac{(a+b)\left(b^2+2 a b-a^2\right)}{a^2+b^2} \)
\(B C=M_1 N_1-M_1 B-C N_1=\)
\(=M N-2 B M \cdot \cos 2 \alpha= \)
\(=a+b-2 b \cdot \dfrac{b^2-a^2}{a^2+b^2}=\)
\(\dfrac{(a+b)\left(a^2+2 a b-b^2\right)}{a^2+b^2}\)
Следовательно,
\(7\left(a^2+2 a b-b^2\right)=b^2+2 a b-a^2 ; \)
\(8 a^2+12 a b-8 b^2=0 ; \)
\(2 a^2+3 a b-2 b^2=0 ; \)
\((2 a-b)(a+2 b)=0,\)
откуда получаем: \(b=2 a\). Таким образом, \(A M: M B=a: b=1: 2\).